緊急倒車模式下螺旋槳誘導環狀渦的發展機理

王超，李鵬，王文全，孫帥

(1.哈爾濱工程大學 船舶工程學院，黑龍江 哈爾濱 150001；2.中國船舶及海洋工程設計院，上海 200011)

以轉速ω、自由來流速度U為變量可將螺旋槳工作模式分為4種[1]：正車前進、正車倒退、倒車前進和倒車倒退。正車前進，ω和U固定時，螺旋槳產生的推力、扭矩不隨時間變化；其余3種工作模式用于艦船操縱，此時，螺旋槳工作流場較正車前進復雜，緊急倒車模式更甚，產生急劇變化的水動力載荷，威脅螺旋槳結構強度，甚至發生塑性變形或損壞其結構，進而造成槳的效率降低、喪失等危險。研究緊急倒車模式下螺旋槳流場特性能全面掌握螺旋槳的性能，同時能指導艦船的安全操縱，亦對指導在非設計工況下保證螺旋槳結構強度安全有重要意義。

HECKER等[2-3]對P4381螺旋槳緊急倒車模式下的載荷、流場開展了實驗，螺旋槳盤面附近存在的1個環狀旋渦，為后續的理論研究提供了驗證基礎；文獻[4-7]基于不同的湍流模型對螺旋槳非設計工況下的流場進行數值計算分析，驗證了環狀渦的存在；他們的研究還將緊急倒車模式下螺旋槳流場特征分為4 個階段：射流環附著階段、穩定環狀渦階段、環狀渦擺動階段、環狀渦脫落及尾流分離階段，并對每類流場與螺旋槳載荷之間的關系進行探討；王貴彪[8]對導管槳緊急倒車模式下的水動力性能進行數值模擬計算，結果表明導管和螺旋槳的推力變化趨勢始終保持一致且變化劇烈；陳進[9]采用LES模擬對螺旋槳緊急倒車和停船正車的螺旋槳性能進行了數值模擬計算。

目前，緊急倒車模式下螺旋槳的推進性能已有較多研究，但針對影響其性能的環狀渦仍缺乏系統的研究成果。本文以E1619槳為研究對象，以Star CCM+為工具，基于大渦模擬(LES)對該槳緊急倒車模式下的流場進行計算，系統分析在重載、均載和輕載狀態下螺旋槳附近的流場特征，總結得出環狀渦的形成原因以及環狀渦變形、演化和脫落與3向速度之間的關系。

1 數值計算方法

1.1 理論方法和湍流模型

緊急倒車過程中，流向相反的流場耦合存在大量的不穩定流動和分離旋渦。大渦模擬[10-11](large eddy simulation,LES)是對紊流脈動(紊流渦)的1種空間平均，通過過濾函數將大尺度渦和小尺度渦分離開，大尺度渦進行直接模擬，小尺度渦用模型來封閉。大渦模擬成立的理論基礎是在高雷諾數紊流中存在慣性尺度的渦，該尺度的渦具有統計意義上的各項同性的性質，理論上它既不含能量也不耗散能量，它將含能尺度的渦的能量傳遞給耗散尺度的渦。LES中，次格子尺度模型較RANS包含更少的經驗系數和定義系數，大渦模擬中用于過濾變量的連續性和動量方程如式(1)所示，當流體計算的網格尺寸足夠小的時候，次格子尺度模型對流動的影響會降至最低，更小范圍內的流體流動，即小于網格尺寸的湍流流動會被次格子尺度模型移除模擬結果。

(1)

式中：xi、xj是單元中心的坐標分量；ui和uj是速度分量的平均值；p是平均壓強；μ是流體粘性系數；ρ是流體密度；τij是網格應力值：

(2)

1.2 計算模型的建立

1.2.1 計算域及網格劃分

E1619槳[12]是七葉大側斜螺旋槳，該槳是意大利INSEAN水池為潛艇設計的專用螺旋槳，其正車運轉時為右旋槳.如圖1(b)所示，螺旋槳直徑D為485 mm，轂徑比0.226，槳葉0.7倍半徑處螺距為1.15，0.75倍半徑處弦長為6.8 mm。本文參考Pontarelli[6]的研究設置計算域尺寸及其邊界條件，如圖2所示。

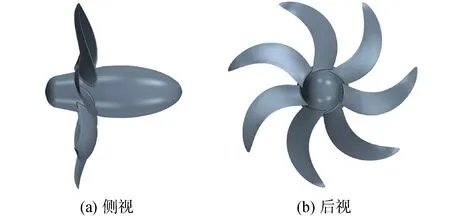
圖1 E1619槳幾何模型Fig.1 E1619 Propeller model

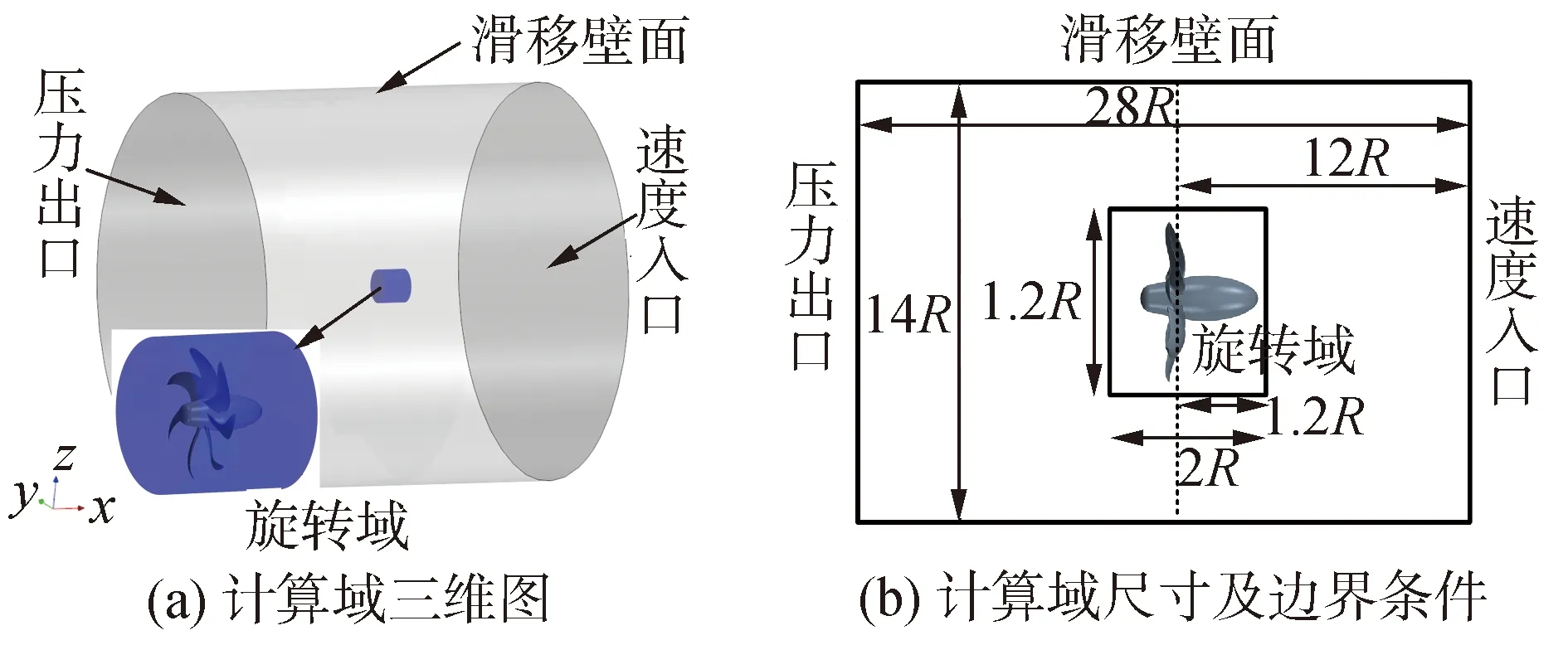
圖2 緊急倒車仿真計算域及邊界條件Fig.2 Emergency reversing simulation calculation domain and boundary conditions

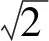
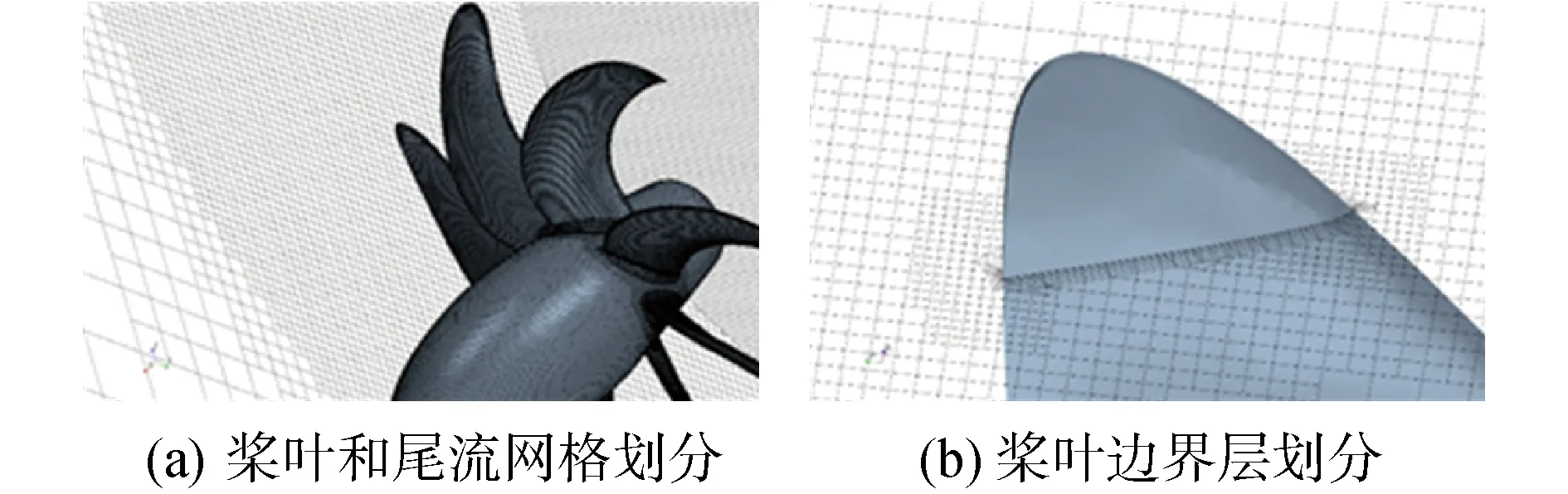
圖3 用于收斂性計算的細網格劃分Fig.3 Fine grid for convergency calculations

表1 收斂性計算的網格數量分布Table 1 The distribution of the number of the number of grids calculated for convergence

1.2.2 計算工況設定

文獻[1-5]的研究中，以螺旋槳倒轉即螺旋槳角速度ω為負、自由來流速度與正車運轉相同即來流速度U為正時定義為緊急倒車運轉。此時E1619槳的運轉模式如圖4所示。緊急倒車模式螺旋槳轉速和來流速度表示無量綱化J為[3-5]:

(3)

式中：U是來流速度,m/s；n是緊急倒車螺旋槳轉速,r/s；D是螺旋槳直徑,m。

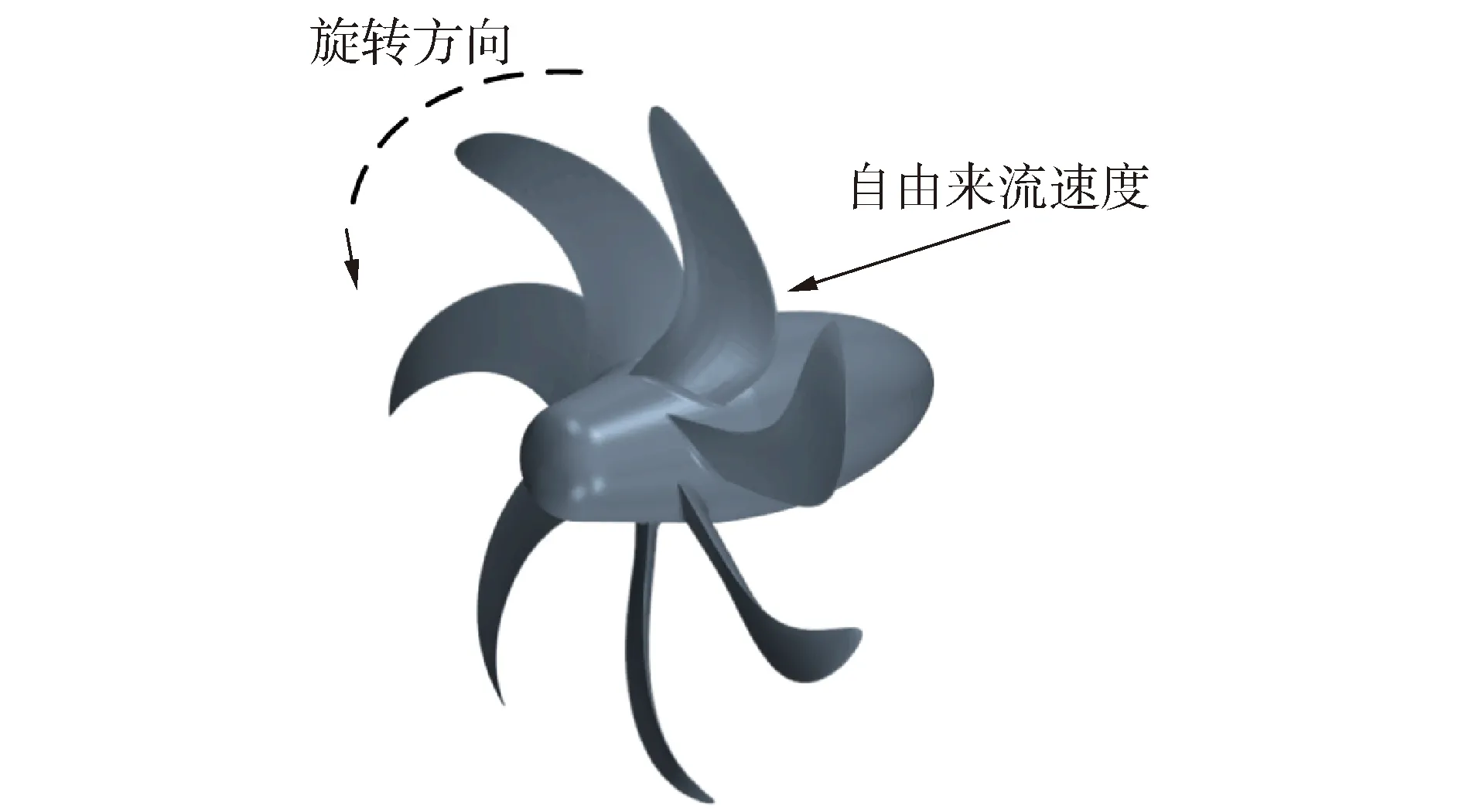
圖4 螺旋槳緊急倒車運轉Fig.4 Crashback for propeller

同時，JESSUP等[4-5]的研究發現，緊急倒車過程中，有3個的載荷作用于螺旋槳，即軸向推力、扭矩和側向力。為區別于正車運轉時螺旋槳載荷，本文以T、TS、Q3個力學元素，利用式(4)～(6)進行無量綱化獲得3個系數KT、KTS、KQ：

(4)

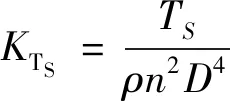
(5)

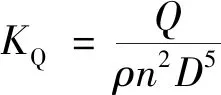
(6)

在J=-0.5時，螺旋槳環狀渦的變形、演化和脫落與其自身性能變化很具有代表性[4-5]，因此本文選定這一特殊的工況進行螺旋槳緊急倒車流場特性的研究。E1619槳的正車額定轉速為23.15 r/s[13]，螺旋槳緊急倒車時的額定轉速均為對應額定轉速的65%～75%[6]，本文中將緊急倒車模式下E1619槳的轉速定為16 r/s，約為正車額定轉速的70%，因此J=-0.5時的自由來流的速度為3.88 m/s。

2 收斂性分析

CFD仿真計算的不確定度主要有3個來源：網格分辨率，時間步長分辨率和迭代次數。文獻[14-16]的研究表明，網格分辨率相對于其他2項對計算結果的影響大1個數量級。本節用3套網格和3個時間步長(Δt/2、Δt和2Δt，Δt為螺旋槳倒轉1°的時間)對J=-0.5時3個力學分量(KT、KTS、KQ)的平均值、最大值和最小值共9個分量進行網格、時間步長收斂性計算。圖5給出J=-0.5不同網格和時間步長時上述9個分量的計算結果，可以看出，9個分量對網格和時間步長的敏感性不高。

網格收斂性驗證方法用STERN等[14-16]的論述過程進行。網格收斂率RG為：

(7)

式中Si(i=1,2,3)分別代表粗、中和細網格對應的計算結果。

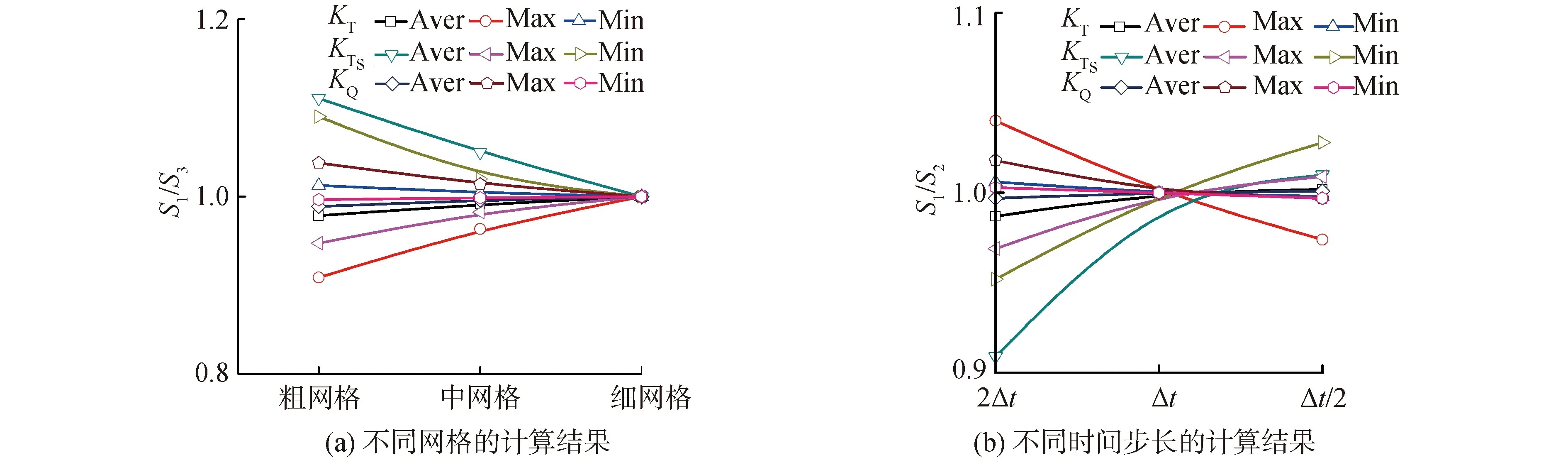
圖5 不同網格和時間步長計算結果對比Fig.5 Comparison of results from different grids and timesteps

表2是網格收斂性驗證的計算結果，可以看出，針對KT、KTS、KQ的平均值、最大值和最小值等9個變量的計算結果得出網格收斂率RG均小于1，同樣基于Fine網格進行的時間步長的收斂率RT同樣均小于1。綜上，本次計算采用的網格和時間步長呈單調收斂，網格及時間步長收斂性很好。另外，本文還基于Fine網格、Δt時間步長進行了E1619槳正車敞水性能的計算，計算結果同實驗值和Di等[13]的仿真結果進行了對比，如圖6所示，可以看出，本文的計算結果和實驗值的吻合程度很高，相比于Di等[13]的計算更為貼近實驗值。

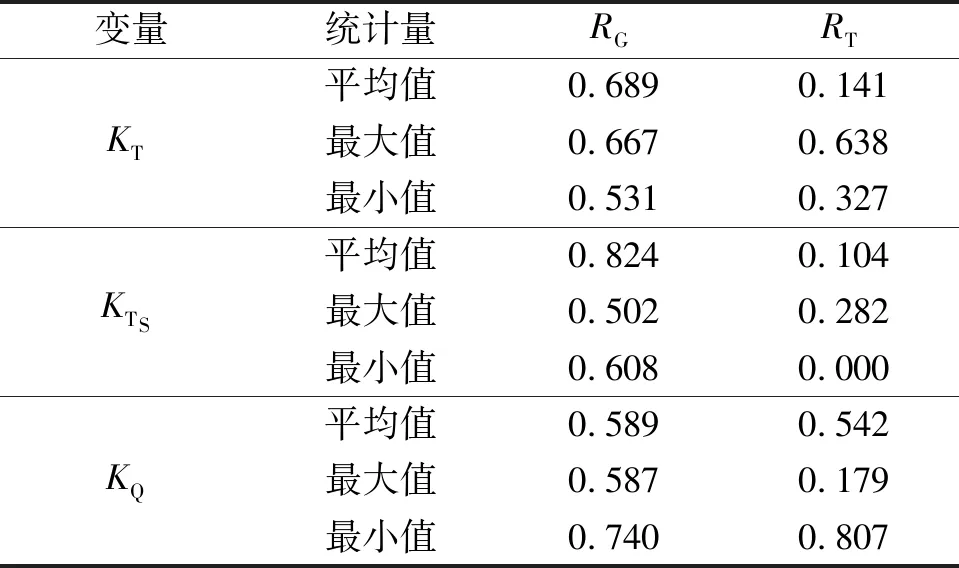
表2 網格收斂性分析Table 2 Convergence analysis of mesh

3 水動力及流場仿真結果分析

3.1 水動力載荷

本次計算中，為避免計算不收斂，螺旋槳共旋轉30圈，采用最后20圈的數據進行分析，圖7是最后20圈的載荷(橫軸為螺旋槳圈數，即旋轉圈數)的3個分量時歷曲線。可以看出螺旋槳的載荷曲線波動很大，在旋轉20圈的過程中沒有出現明顯的周期性循環，KT和KQ的變化趨勢除數值外基本相同，但KT的變化較兩者有著明顯區別，由此可推斷KTS的變化較KT和KQ的影響為微量；將載荷時歷數據進行數學方法處理，可以獲得其平均值、標準差(如表3)。參考文獻[17-19]的研究方法，以1倍標準差為單位，可以看出載荷時歷曲線在平均值周圍的波動情況，如圖7所示。本文將位于平均值±標準差外的載荷稱為極限載荷，反之為平均載荷，極限載荷按絕對值大小分為重載和輕載。可以看出，3個力學分量的變化趨勢基本相同，在對應的時刻均出現極限載荷或平均載荷，為后續分析提供了途徑。

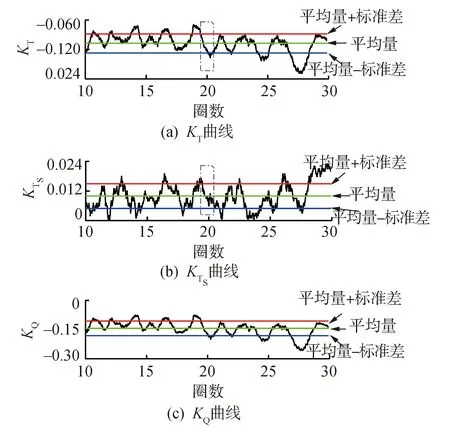
圖7 載荷時歷曲線Fig.7 Load time domain curves

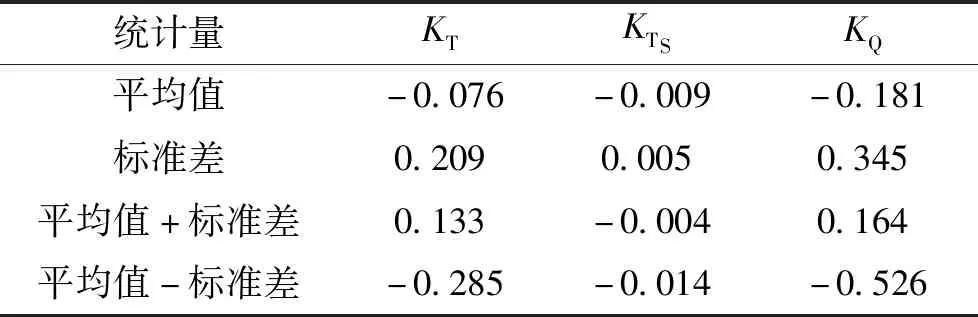
表3 載荷統計數據Table 3 Load statistics

3.2 全局流場分析

螺旋槳載荷分為極限載荷和平均載荷，圖7中表明在20圈左右時，螺旋槳的3個載荷分量均出現了重載、均載和輕載的循環，本文針對這一過程進行分析。如圖8所示以KT為例，對應圖7中矩形虛線框中部分，A、B、C對應了3.1節中的輕載、均載和重載3個工況，圖9是3種工況下螺旋槳盤面附近低壓等值面的軸向速度云圖。

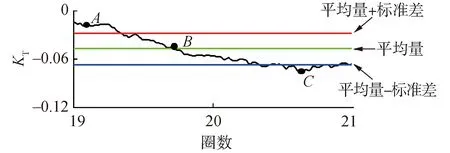
圖8 KT時歷曲線中的極限載荷、平均載荷Fig.8 Time domain curve of KT consisting high-load,mean-load and low-load

在1個載荷循環內，螺旋槳周圍存在1個明顯的環狀流場渦結構，下文簡稱環狀渦。可以看出：環狀渦結構緊湊、直徑較小且變形微弱時的水動力載荷最小，如圖9(a)所示；環狀渦結構緊湊，但其內環中心發生偏移，外環出現低壓凸起，此時螺旋槳載荷循環的均值，如圖9(b)所示；環狀渦內環部分完全脫離槳葉，其結構發生明顯的變形，同時其外環凸起即將發生或發生脫落時，螺旋槳處于載荷循環的極大值；外環凸起脫落完成后，環狀渦的結構再次回歸完整緊湊。環狀渦的槳葉葉面的低壓區沒有明顯的變化，但葉背的低壓區面積與槳葉載荷呈正比例變化，即變形、演化對應螺旋槳的水動力載荷變化，同時槳葉表面的低壓區亦表現出這樣的趨勢，圖9中可以看出，無論是哪種載荷工況，載荷增加，低壓區面積有明顯增加，且低壓區不斷向葉根處擴展。

圖9 不同載荷工況下螺旋槳附近流場(低壓-25 kPa等值面的軸向速度云圖)Fig.9 Flow field near propeller under different load cases(isosurface of P=-25 kPa colored by axial velocity)

緊急倒車模式下，螺旋槳的排出流和自由來流流向相反，在螺旋槳上游流場產生擠壓、剪切，從而沿螺旋槳徑向流動，形成上游的匯聚流；螺旋槳吸入流同樣和自由來流流向相反，在螺旋槳下游形成分離流；匯聚流和分離流的流動在螺旋槳盤面附近形成了旋渦狀的流場流動，如圖10(a)所示，在三維空間內對應形成如圖9所示的環狀渦。圖10(b)是J=-0.5時，不同載荷工況螺旋槳上下游5個軸向位置的流場速度曲線，可以看出不同載荷工況下，流場的軸向速度發生較大的變化，推斷匯聚流和分離流形成的旋渦大小、位置會有所不同，進而形成三維空間內環狀渦的變形、演化，甚至是脫落。

圖10 環狀渦的形成原理Fig.10 A schematic diagram of the formation of the ring-vortex

3.3 局部流場分析

緊急倒車時極限載荷和環狀渦的變形演化有著密切的關系，而環狀渦的形成、變形和演化均與流場速度相關。圖11是環狀渦近后方(螺旋槳下游)、環狀渦中心處及近前方1.5倍半徑內流場(依次對應圖10(a)中從左向右3條垂直實線對應的切面)的軸向、徑向和切向速度。輕載時環狀渦的直徑明顯小于重載，此時近前方徑向速度為正值、近后方切面的徑向速度為負值，且絕對值明顯較小，對應圖10(a)可知，在同一來流速度下，輕載時的匯聚流和分離流速度相對于來流的速度要小于重載，由此形成了較小的環狀渦。重載時，在環狀渦出現脫落的地方，如圖11(a)中所示2處，2項速度在渦脫落的對應徑向投影位置出現了符號相反，即速度矢量相反的流場，稱之為“流場速度脊線”；對比輕載工況，徑向速度、切向速度等值線更加的完整和緊湊，且未出現“流場速度脊線”，對應環狀渦更加的完整和緊湊，推斷環狀渦的脫落與“流場速度脊線”的出現有關。緊急倒車模式下，螺旋槳處于高雷諾數流場中，而“流場速度脊線”處相反的軸向速度和切向速度迫使環狀渦的凸起發生剪切，從而形成了環狀渦的脫落，如圖12(a)所示；結合對環狀渦3個截面的3個方向速度分析可知，環狀渦的變形與其附近流場徑向速度的不均勻分布有關，輕載時徑向速度分布均勻、大小相似，重載則相反，對應于環狀渦的變形。

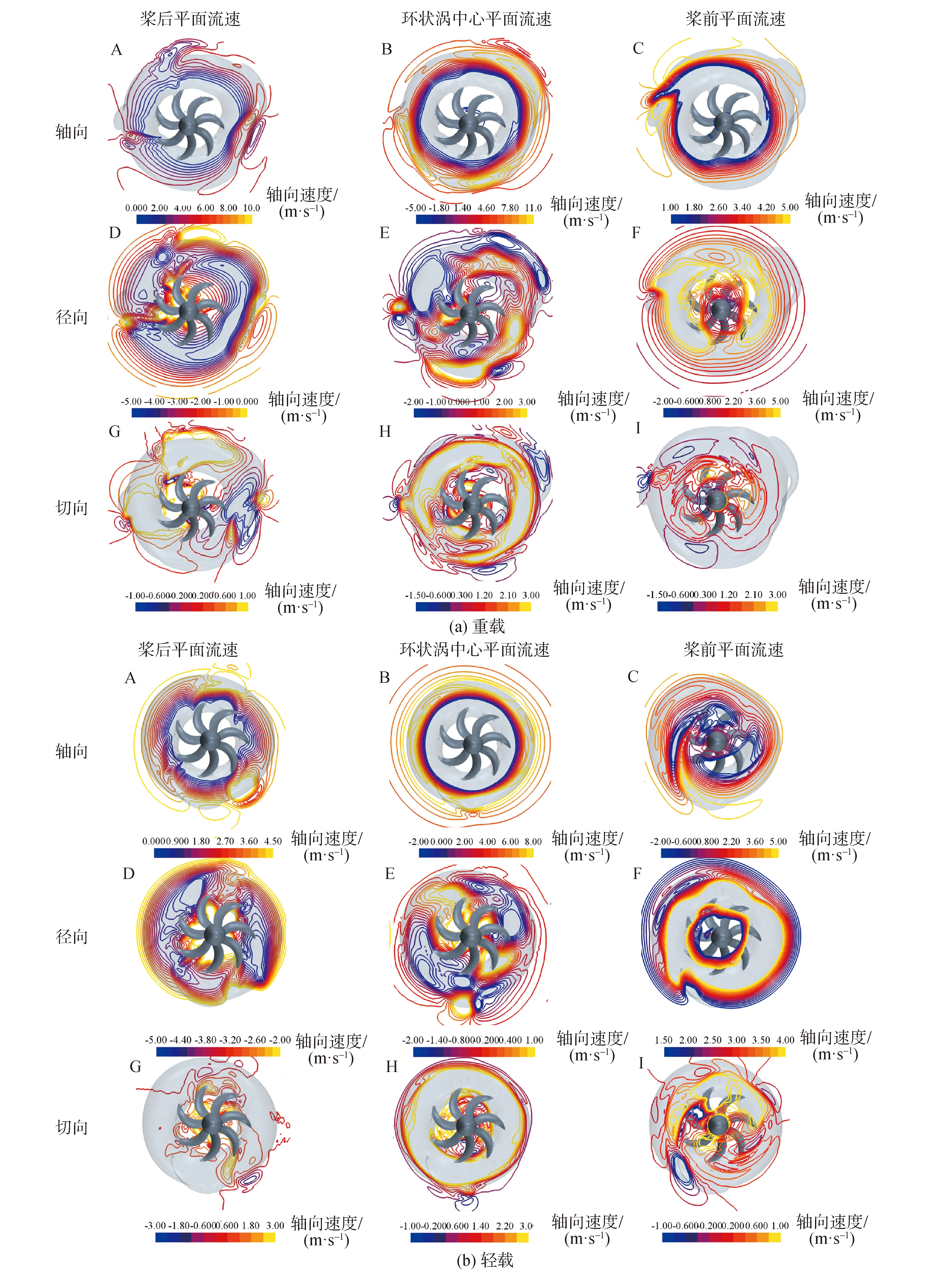
圖11 不同載荷工況3個軸向切面的3向速度Fig.11 Different velocities at 3 axial locations under different cases

圖13是3個不同半徑切面，波動最為劇烈的槳葉附近流場矢量圖。可以看出，沿螺旋槳徑向方向，槳葉附近的流場波動程度逐漸降低，且隨邊處出現了不同程度的湍流旋渦，但重載工況時更為明顯，尤其在0.4倍半徑處。結合圖9推斷這可能是造成槳葉表面低壓區不同擴展程度的原因。另外,隨邊處波動劇烈的流場也能造成槳葉受力的波動，由此推斷也是緊急倒車模式螺旋槳載荷波動的原因。表4是1倍半徑環狀渦中心處平面(下文稱中面)緊急倒車時，重載工況和輕載的轉換造成中面內的流場通量不同(流場面積分量)，另外中面3向速度的標準差也有不同程度的波動情況，在較大的通量和波動程度下，即重載時，螺旋槳的載荷必然大于通量和波動程度較小，即輕載工況。另外，3向速度分量中，切向速度的波動程度最大，結合圖12中的環狀渦脫落簡圖可推斷，切向速度對于環狀渦的脫落較軸向速度有較大的作用，而環狀渦表面的凸起或脫落渦多沿其周向較長亦說明了這一點。

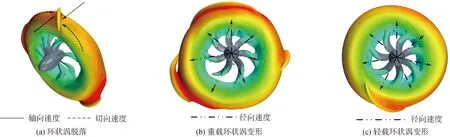
圖12 環狀渦變形演化原理Fig.12 Sketch of the deformation and evolution of ring-vortex

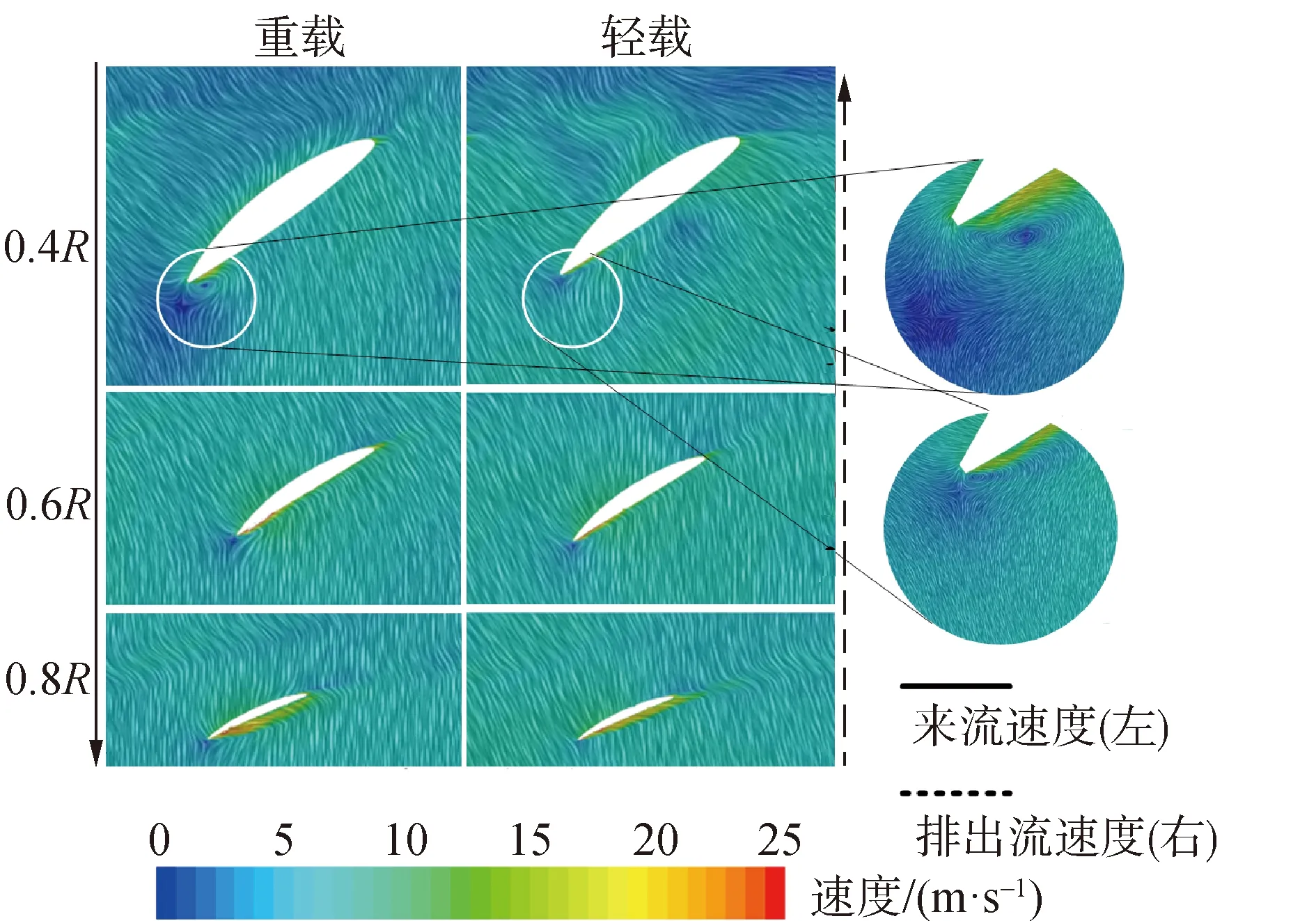
圖13 不同半徑處槳葉局部流場矢量Fig.13 Vector velocity of local field at different radial locations

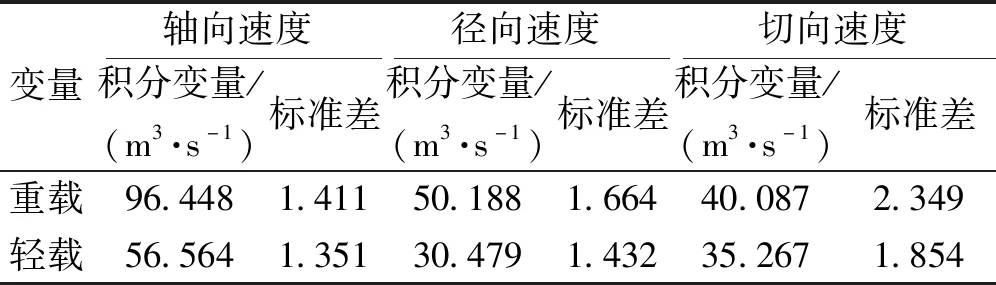
表4 螺旋槳中心平面流場主要參數Table 4 Main parameters of the field in the middle plane of the propeller

4 結論

1)通過網格、時間步長收斂性的驗證分析發現，以Star CCM+為工具，基于LES湍流模型計算緊急倒車模式下螺旋槳性能具有可行性和正確性。

2)緊急倒車模式下，螺旋槳的KT、KTS、KQ變化劇烈且無規律、周期，且螺旋槳盤面附近存在1個不斷變形、演化和脫落的環狀渦；環狀渦的形成是螺旋槳排出流和自由來流擠壓、剪切而引發的匯聚流和分離流共同作用的結果。

3) 極限載荷和平均載荷的變化與螺旋槳附近環狀渦的變形和演化有關，環狀渦附近流場的“速度脊線”是造成切向速度和軸向速度的剪切形成了其凸起和脫落，徑向速度的不均勻性造成其變形。

本文對緊急倒車模式過程的流場進行了準定常計算分析，即特定J時的流場特性，初步得出螺旋槳附近環狀渦的存在是該過程中的重要特征；另外，環狀渦的變形、演化和脫落影響螺旋槳的載荷的變化。但未來仍需要進行更細致的工作，即對不同J下螺旋槳盤面附近的流場及其變化規律進行深入的探討。