橋梁轉體施工接觸面應力分析及優化方法

黃仕平，唐勇，袁兆勛，黃永輝，胡俊亮

(1.華南理工大學 土木與交通學院，廣東 廣州 510640；2.清華大學 摩擦學國家重點實驗室，北京 100084；3.廣州大學 廣州大學-淡江大學工程結構災害與控制聯合研究中心，廣東 廣州 510006；4.中鐵大橋科學研究院有限公司，湖北 武漢 430034；5.橋梁結構健康與安全國家重點實驗室，湖北 武漢 430034)

轉體施工法在跨越溝壑、峽谷等復雜地形條件下具有獨特的優勢[1]。其主要工作原理是將位于不利地形上的橋梁分成2個半跨，每個半跨結構均在河流的兩岸，或在與跨越的障礙物平行的位置處施工，施工完成后再通過轉動，將2個半跨結構同時旋轉到位。轉體施工法的出現，突破了傳統橋梁建設技術的地理局限，使得橋梁建設可以挑戰更加復雜的地形。此外，轉體施工法在跨越已運營線路時能夠安全、快速進行施工，避免對既有線路的運營造成影響，節省人力物力，產生更好的社會經濟效益。轉體裝置是轉體施工中的核心組成部分，該裝置的接觸面在安裝和轉動過程處于高應力狀態。接觸面中的高應力狀態有可能使材料出現磨損，在轉動過程中出現鎖死現象，導致轉動失敗，甚至有可能在轉動過程偏移原位引起傾覆[2]。因此，接觸面的應力分析及接觸界面設計是轉體施工成功的關鍵工作。轉體裝置一般采用球鉸，其接觸屬于協調接觸。協調接觸應用廣泛，一直是工程界和學術界的研究重點。Ciavarella等[3]推導了圓柱形協調接觸的理論解，Hu等[4]提出了圓柱面協調接觸的彈塑性模型，Fang等[5]給出了協調和非協調接觸面的半解析解。文獻[2-5]利用有限元技術對協調接觸進行數值研究。為了在轉動過程減小摩擦阻力，轉動裝置在接觸面引入了摩擦系數較低的滑塊，然而現有研究忽略了接觸面上嵌入的滑塊[6-7]，難以體現接觸面上的真實應力分布。

本文以轉體裝置的接觸面為研究對象，在考慮了滑塊的影響下，提煉出簡化的接觸力學模型，分析接觸面的應力分布規律，并對滑塊的空間分布作進一步的優化，旨在控制其在安裝、轉動過程中的應力狀態，為接觸界面的設計提供理論基礎。

1 轉體裝置接觸模型簡化及應力分析

1.1 轉體裝置構造

轉體施工法的關鍵技術問題是對轉體系統受力狀態的控制，其實質是大型接觸體在高壓狀態下的接觸問題。典型轉體系統構造如圖1所示，其由上轉盤、下轉盤和牽引系統組成。嵌固于下轉盤的凹球面與上轉盤的凸球面相互配合，共同組成一對接觸面，下轉盤的凹球面由內到外嵌入環形布置的若干聚四氟乙烯(PTFE)滑塊，聚四氟乙烯是摩擦系數(0.05～0.1)極低的材料，能顯著降低轉體過程中的摩擦阻力。

本文以茂湛鐵路跨線橋為例，該橋全長2 037.5 m，主橋采用雙幅(75 m+75 m)T型剛構橋，分左右2幅。為減少工程施工對既有鐵路運營的影響，采用轉體施工方法。2幅橋分別在鐵路兩側平行于鐵路預制，轉體施工時雙幅同步轉動，轉體角度為83.6°，如圖2所示。其中，單幅橋轉體重量約10 500 t，每個球鉸布置12環共634片半徑為3 cm的PTFE滑塊，滑塊的設計抗壓強度為100 MPa。滑塊現場布置情況如圖3所示。

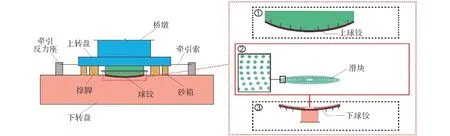
圖1 轉體系統構造Fig.1 The construction of rotating system

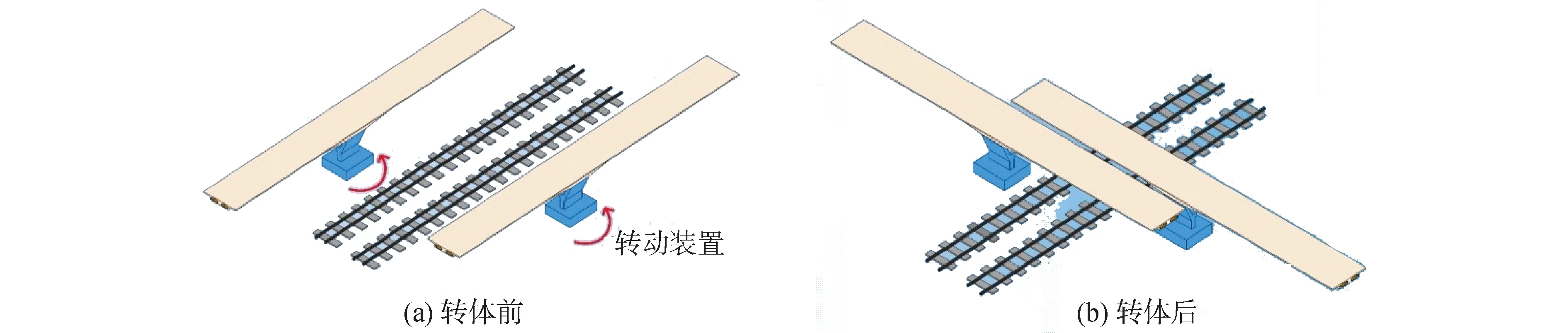
圖2 轉體施工法示意Fig.2 Illustration of the rotation superstructure construction method

1.2 接觸模型的簡化

從復雜的轉體裝置中提煉出接觸模型，不僅可以節省大量的建模工作，還為后續有限元模型的求解節省了大量計算時間。本文對上述復雜的接觸問題進行簡化。接觸問題(如圖4所示)區別于一般固體力學問題之處，在于其有獨特的附加約束，即接觸約束條件。由于接觸過程中接觸約束條件不斷發生變化，計算接觸力學一般采用增量法。基于有限元的計算接觸力學與一般有限單元法的差異，在于對附加約束的處理。粘結狀態下接觸問題的接觸約束條件為：

(1)

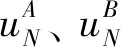
(2)

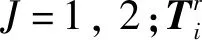
(3)

式中：第1項是虛應變能；第2項是面力產生的外虛功；第3項是約束變量λ(拉格朗日乘子變量)產生的“虛功”。式(2)和(3)是等價的，同時包含了接觸界面上等效結點力和拉格朗日乘子變量間的關系。若對整個區域進行離散化，用結點位移作為形函數的基本變量，其最終有限元求解方程為[8]：

(4)

式中：KL是接觸體整體剛度矩陣的線性項；KNL是相應的非線性項;Kcλ是界面約束剛度；QL為等效結點載荷向量。式(4)中第1項等式實質是式(3)的離散化形式，第2項是約束條件(1)的離散化形式。由式(1)～(4)可見，在求解接觸方程之前，首先需要在離散化后(即接觸界面離散成單元結點)的接觸邊界中，搜尋滿足接觸約束條件的接觸結點，即判斷2個接觸點的最短距離gN是否滿足接觸約束條件。要獲得潛在的接觸點，需要在每個增量步中根據位移增量重新調整接觸體A、B的坐標，然后根據式(1)進行計算。研究表明，接觸對的搜尋通常占總分析時間的40%～50%[8]。本文提出簡化接觸面的思路，即根據現有接觸理論[9-12]，把2個彈性接觸體的接觸，簡化成1個剛體和1個彈性體的接觸。由于剛體僅有剛體位移增量，不存在彈性位移增量，因此在每個增量步中僅需要迭代新彈性體的位移增量，這將大大減小搜索時間。

圖3 聚四氧乙烯滑塊現場布置Fig.3 The layout of the PTFE slide plates on site

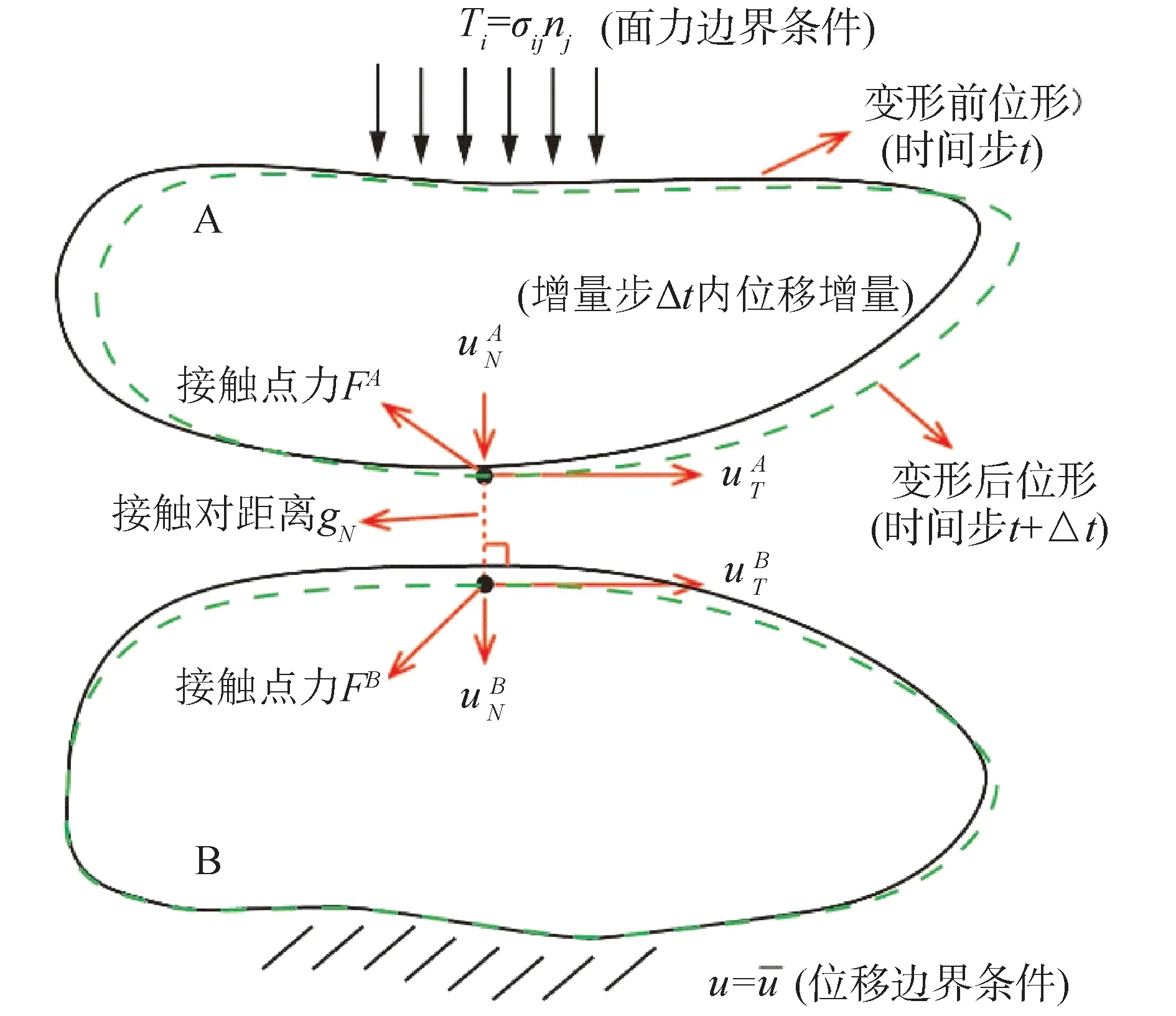
圖4 典型的接觸問題及邊界條件Fig.4 Typical contact problems and boundary conditions

本文把2個彈性體簡化成1個等效曲面剛體和1個水平光滑彈性體接觸。等效剛體的表面形狀函數，即高度函數為H(x,y)，系2個等效前彈性體的復合高度之和[11]:

H(x,y)=H1(x,y)+H2(x,y)

(5)

式中：H1為等效前彈性體1的表面形狀函數，H2為等效前彈性體2的表面形狀函數。等效后的光滑彈性體的材料參數為：

(6)

式中：E1、v1為等效前彈性體1的彈性模量和泊松比；E2、v2為等效前彈性體2的彈性模量和泊松比。根據接觸力學理論，對轉體裝置的接觸問題進行簡化，旨在降低轉體接觸面分析的建模成本，提高接觸模型計算效率，同時為后續優化轉體接觸面有限元分析提供支持。

轉體施工的接觸模型實際為上球鉸(鋼材)與下球鉸所嵌入的PTFE滑塊之間的彈性接觸，接觸模型如圖5(a)所示。以茂湛鐵路跨線橋為例，下球鉸的球面半徑R為8 m，上球鉸的球面半徑R′為7.992 m。滑塊上表面所形成的球面半徑與上球鉸球面半徑相同，其凸出下球鉸上表面的高度h，等于下球鉸球面半徑R與上球鉸球面半徑R′之差，即0.008 m。由于轉體裝置的旋轉對稱性，可將三維空間問題轉化為二維平面問題，即只需考慮x方向，高度函數H(x,y)可簡化為H(x)。以上球鉸和滑塊上表面所成球面中心接觸點作為原點，分別建立上、下轉盤結構局部坐標系，坐標軸方向如圖5(a)所示。

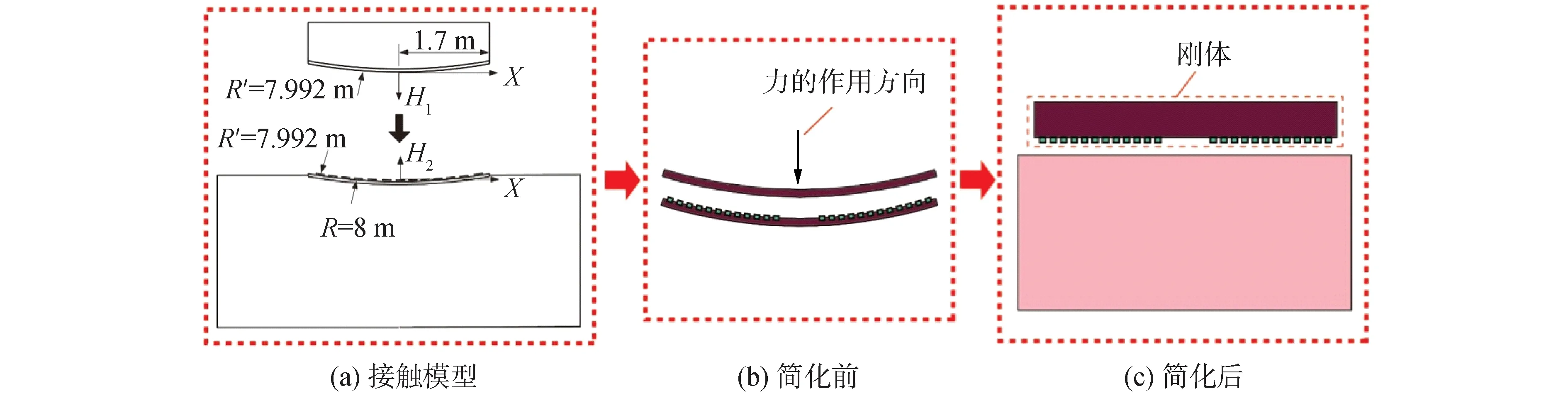
圖5 接觸模型示意Fig.5 Illustration of the contact model

對于上轉盤結構，幾何關系為：

x2+(H1+R′)2=R′2

(7)

由此可得高度函數H1為：

(8)

由圖5中幾何關系，易知上式第2項應取“+”號，即：

(9)

對于下轉盤結構，由于PTFE滑塊的存在，使得下轉盤表面分成2種不同的形式，在局部坐標系下，滑塊、下球鉸分別由幾何關系可得：

x2+(H2-R′)2=R′2

(10)

x22+(H2-R′)2=R2

(11)

可得高度函數H2為：

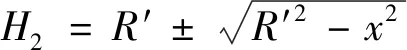
(12)

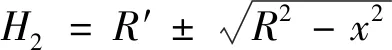
(13)

綜合以上2式及幾何關系，可得下轉盤高度函數H2的綜合表達式為：

(14)

綜上，復合剛性曲面高度函數H的表達式為：

(15)

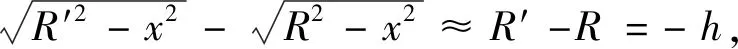
(16)

分析式(16)的幾何意義可知，接觸模型經過簡化，等效為平面內分布的滑塊與圓柱體(半徑與球鉸投影半徑相等)共同構成的剛體，和1個表面水平的彈性體之間的接觸模型，其中滑塊的高度為h。接觸模型的簡化過程如圖5(b)、(c)所示。

1.3 簡化模型在有限元分析的應用

本節以茂湛鐵路跨線橋為工程背景，驗證本文提出的簡化理論在有限元分析[8,13]時的優勢及正確性。根據表1中的參數，采用ABAQUS有限元軟件分別建立簡化前的接觸模型和簡化后的接觸模型[14-17]，單元類型均為C3D8R，如圖6所示。簡化前的接觸模型為上球鉸與下球鉸所嵌入的PTFE滑塊之間的彈性接觸，簡化后的模型則變為剛體和彈性體間的接觸。

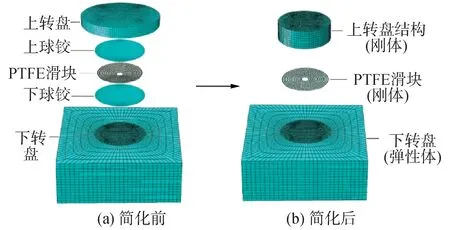
圖6 轉體系統有限元模型示意Fig.6 The model of rotating system

根據式(6)的理論，選定簡化模型的下轉盤彈性體材料泊松比為0.35 (即下球鉸泊松比和PTFE滑塊泊松比的算術平均值)，彈性模量由式(6)確定。實際工程中，考慮到轉體系統配重后，梁體偏心距較小，因此可視上轉盤結構處于中心承重狀態，將10 500 t的轉體重量轉化為均勻面荷載施加于上轉盤結構上表面。下轉盤底面施加固結邊界條件。

由于球鉸和滑塊是最為關鍵的部件，應當劃分較細的網格。通過對網格尺寸效應進行對比分析[18]，最終采用的網格尺寸如下。簡化前的模型：球鉸網格尺寸為40 mm，單個球鉸單元數量為14 336；滑塊網格尺寸為6 mm，單個滑塊單元數量為186；對于上、下轉盤，與球鉸接觸區域混凝土采用較細網格，網格尺寸為60 mm，外圍混凝土采用較粗網格，網格尺寸為200 mm，下轉盤單元數為19 484，上轉盤單元數為13 658；簡化后的模型：對于滑塊和上、下轉盤，其簡化后的網格尺寸與簡化前保持一致。簡化前的總單元個數為179 738，簡化后的總單元個數為139 352。簡化前后，由于單元個數及接觸類型發生變化，且接觸對搜索效率增加了近1倍，總的分析時間減少了近90%。可見，簡化模型在有限元分析時有巨大優勢。

圖7展示了每環滑塊(共12環，634個)的平均接觸應力，即各環滑塊法向接觸合力與其總接觸面積的比值。可見，簡化模型和原模型接觸面壓應力結果基本吻合，最大相對誤差僅為5%。兩者無法完全重合的原因為：簡化前后的幾何模型已經改變，兩者自然無法獲得完全一樣的網格分布，因此應力存在部分差異是合理的。由此可見，本文提出的簡化模型是正確的。

圖7 簡化前后各環平均接觸應力對比Fig.7 Comparison of the average contact stress for different rings of slide plates before and after simplification

2 應力優化方法

2.1 優化方法

由圖7可見，各環滑塊的平均接觸應力極不均勻：滑塊平均接觸應力的大小總體上隨距球鉸中心距離的增大而不斷增大，最小值出現在第3環滑塊，其平均接觸應力值為40.40 MPa；最大值出現在最外環滑塊，對應93.50 MPa。因此，各滑塊的空間分布有待進一步優化。例如，第1環至第9環滑塊的平均接觸應力在理論平均應力曲線下方，說明前9環滑塊的安全度有富余，因而個數可以適當減少；第10環至第12環滑塊的平均接觸應力在理論平均應力曲線上方，說明后3環滑塊的應力較均值偏大，因而個數可以適當增加。各環滑塊的平均接觸應力與理論平均應力的差值，一定程度上反映了接觸面積的盈缺量，進而體現了滑塊個數的富余或不足。其中，理論平均應力為簡化后模型轉體總重量與所有滑塊下表面面積總和的比值。通過以上分析，提出本文的優化目標為：在單個滑塊的平均接觸應力不超過其設計抗壓強度，且每環滑塊的平均接觸應力趨于均勻的情況下，讓滑塊的總個數N盡可能小。具體的優化方法思路如下：1)在滑塊總接觸面積不變的情況下，使每環滑塊的平均接觸應力趨于均勻，通過每環滑塊應力與理論平均應力的差值來調節該環滑塊的數量；2)在保證各環滑塊平均接觸應力分布均勻的情況下，按照優化后的最大應力與優化前的最大應力比值，相應地逐環減少冗余滑塊數。

優化設計是在初步設計的基礎上進行的，初始滑塊的數量取決于轉體的總重及單個滑塊的承載力，單個滑塊的尺寸及承載力往往由制造商提供，取決于制造的難度和施工的便利。初始參數一般由經驗給出，本文優化設計的初始參數來自上述茂湛鐵路跨線橋，其中滑塊的半徑為30 mm，總高18 mm，凸出下球鉸上表面的高度為8 mm，設計抗壓強度為100 MPa，共12環，各環滑塊個數的初始值如表2所示。具體的優化步驟為：

1)計算理論平均應力P0：

(17)

式中：G為轉體總重；r和N分別為滑塊半徑及總個數。

2)通過有限元方法計算簡化模型得到各環平均接觸應力Pi，相應地增減各環滑塊的數量Δni：

(18)

式中：“[ ]”為取整符號；ni和Pi分別對應各環滑塊的個數及平均接觸應力。

3)調整后的各環滑塊個數為：

(19)

式中上標j表示迭代的次數。

4)重復步驟2)、3)，進行迭代計算，直到獲得趨于均勻的應力。

(20)

通過上述步驟，便可得到最終調整后的每環滑塊個數nend，i。

2.2 結果分析

圖8是經過一次迭代后的茂湛鐵路跨線橋各環滑塊的平均接觸應力結果。

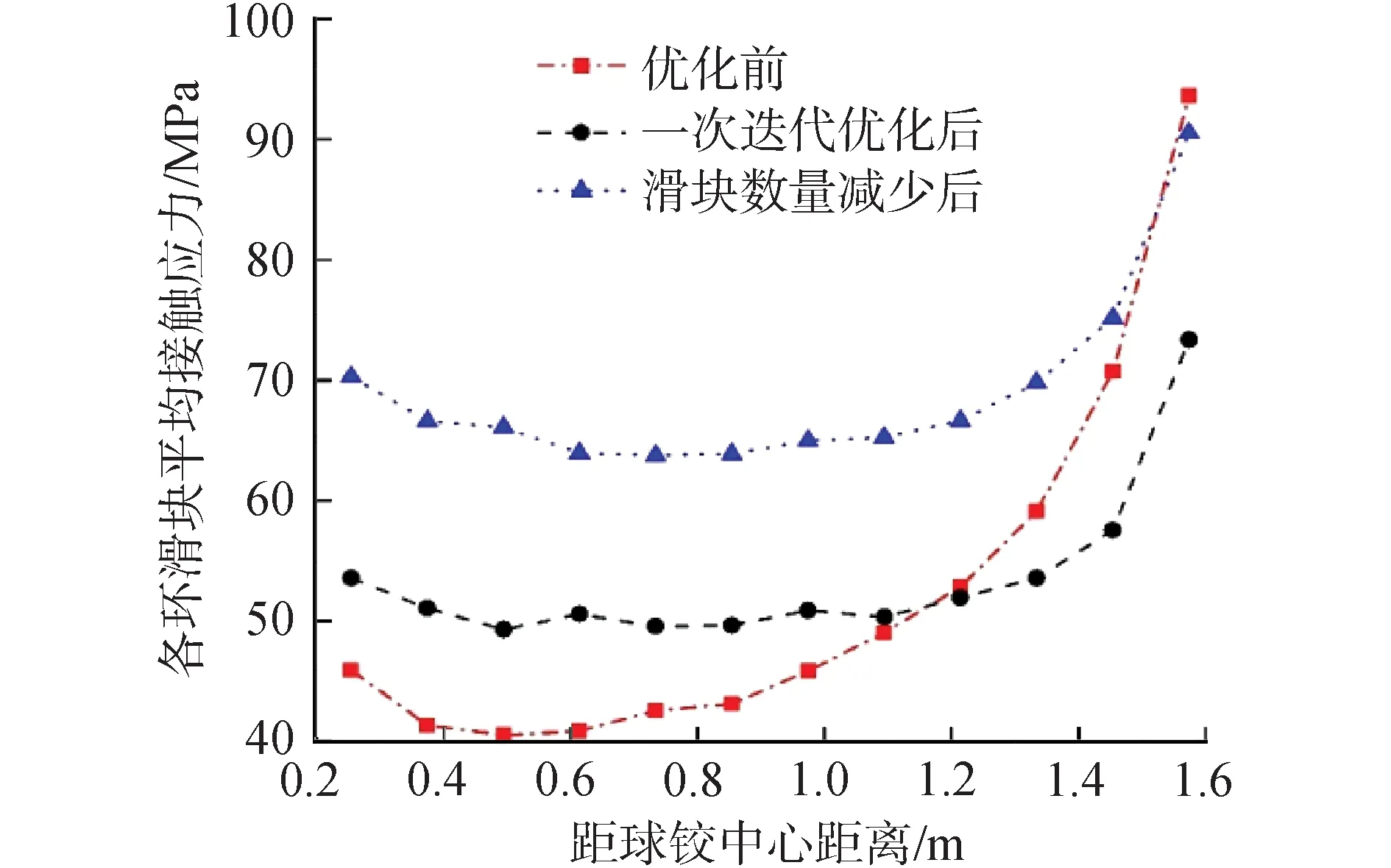
圖8 優化前后PTFE滑塊應力分布情況Fig.8 Stress distribution at each PTFE slide plate for the original model and the optimal model

如圖顯示，經過一次迭代優化后，滑塊的平均接觸應力明顯比優化前均勻。最外側滑塊的平均接觸應力由原來的93.50 MPa降低至73.23 MPa，其余各環滑塊的平均接觸應力約為52 MPa，應力分布已經趨于均勻。并且內側滑塊的平均接觸應力相比優化前有所增加，提高了內側滑塊的材料利用率。可利用同樣的方法，對滑塊的分布進行二次迭代優化。然而二次迭代后，最外環滑塊的個數已經超出球鉸所能容納的范圍，故不再進行下一次迭代。

由于優化后滑塊的最大平均接觸應力為73.23 MPa，遠小于優化前的93.50 MPa，因此可以考慮減少滑塊的數量。根據前面所述方法，按照優化前后的最大應力比值，相應地減少每環的滑塊個數，即在1次迭代后每環滑塊個數的基礎上，對每環的滑塊個數相應地乘以應力比例系數73.23/93.50，得到每環最終優化后的數量。優化后的數量僅為優化前的78%，大幅減少了滑塊數量。通過有限元軟件驗算，由圖8可見，按應力比例減少滑塊個數后的應力曲線，大致等于一次迭代后的曲線整體往上平移16 MPa，且接觸應力分布的均勻程度與一次迭代后的結果保持較好的一致性。最終優化后的滑塊分布與優化前的對比如圖9所示。相應地，表2為優化前后對應每環的滑塊個數及平均接觸應力。由此可見，本文提出的優化方法有效。

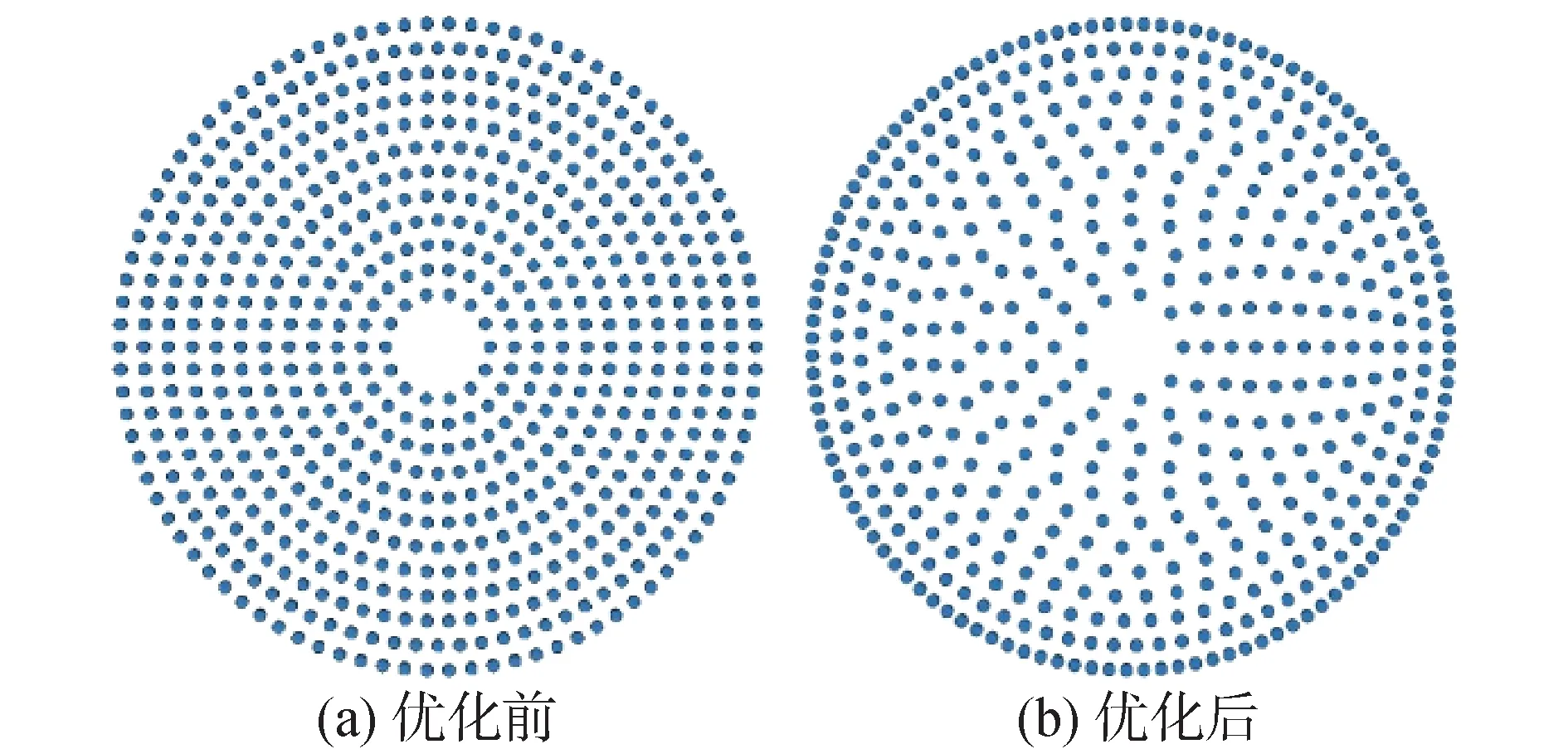
圖9 優化前后滑塊分布Fig.9 The slide plates distribution for the original model and the optimal model

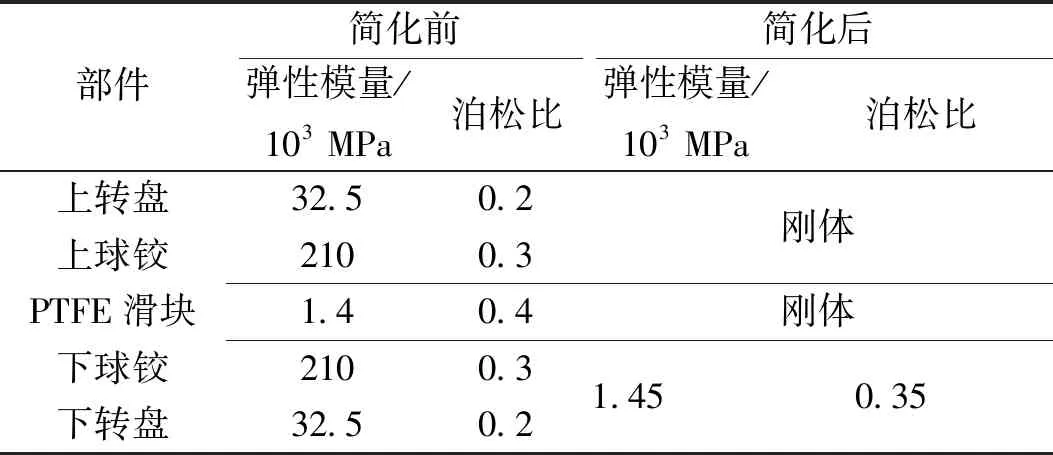
表1 有限元模型參數Table 1 Parameters of the FE model

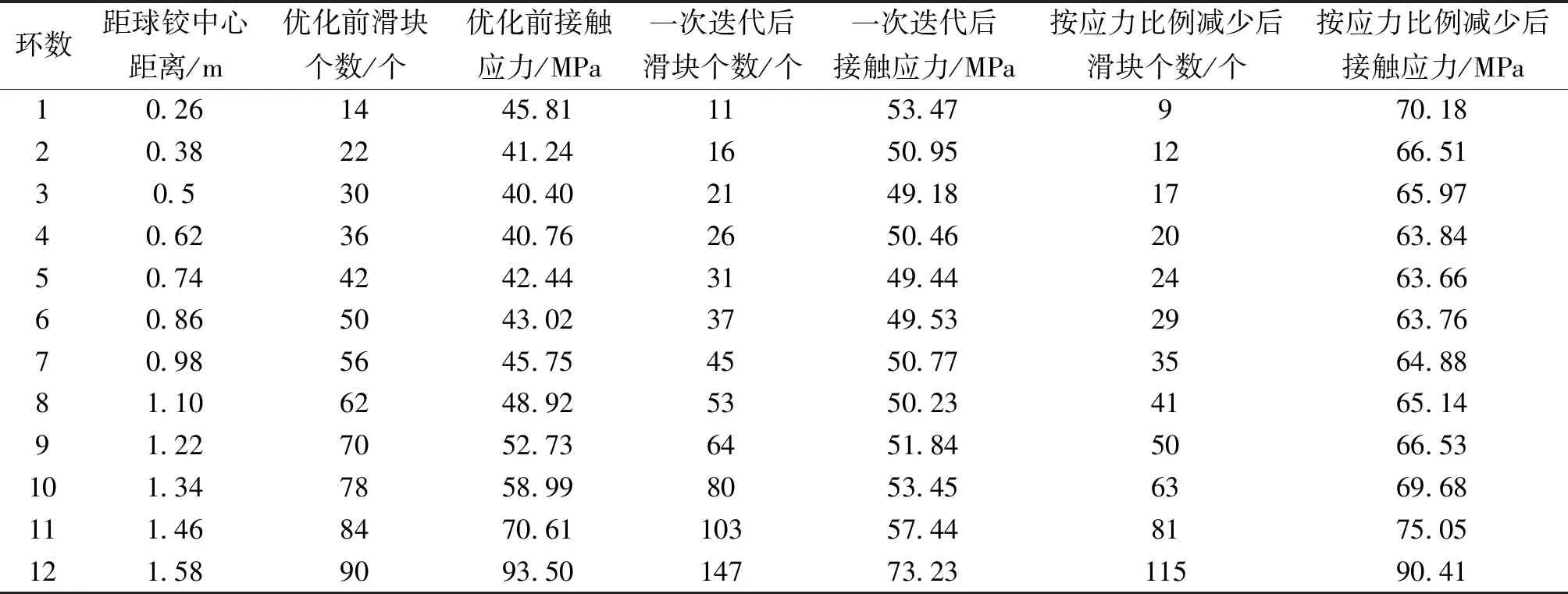
表2 滑塊應力及個數分配Table 2 The contact stress and number of the slide plates

3 結論

1)常規接觸模型經簡化后，可等效為平面內分布的滑塊與圓柱體共同構成的剛體和1個表面水平的彈性體之間的接觸模型；相比常規接觸力學模型，簡化后的計算效率提高了近10倍；簡化前后接觸面壓應力結果基本吻合，最大相對誤差僅為5%。

2)利用簡化后的接觸力學模型對滑塊的空間分布進行優化。優化后，滑塊的數量減少了22%，其應力分布較優化前明顯均勻化，邊緣應力集中效應大大降低，使材料的力學性能得以充分發揮，為轉體施工橋梁往大跨度、大噸位的方向進一步發展提供方法。