整體思維在小學數學中的應用

馬婕

【摘 要】整體思維是數學思維的重要形式。本文就整體思維在小學數學中的一系列表現，如：整體代入、整體聯想、整體替換等。突出在小學數學學習中整體思維的重要性，并對其進行了簡單的探討。

【關鍵詞】整體思維;整體聯想;整體構造

在整個小學數學的學習中，學生會進行很多的思維活動，如：數形結合、發散思維、推理能力等，培養用數學的眼光解決問題，而整體思維就是其中不可或缺的一種。通過對整體思維的學習，孩子不僅可以發現數學解題方法的多樣，也可以發現數學的簡潔美;在平常生活中，整體思維好的孩子，也能從整體、從大局著手處理問題，不是只看問題的局部或個體。因此，研究整體思維在小學數學中的應用，顯得極其重要。

一、整體思維的定義

整體思維在辯證法中，又叫做系統思維，它認為事物是由各個局部按照一定的秩序組織起來的整體，在解決問題時人們應該持有整體或者全面的觀點，不能以偏概全。

在數學中，整體思維又被稱為整體思想，就是要求我們在解決數學問題時，應該從問題的整體性質出發，善于用整體、全面的眼光，把握各方面的關聯，將問題作為一個整體去思考，尤其突出對問題整體結構的分析，從而抓住問題的內在聯系，進行有目的、有意識的探索，從而找到解決問題的途徑。

整體思維在數學教學中一直存在，從我們小學學習的化簡與求值，到初中學習的解方程組，再到高中學習的等差等比數列，從代數到幾何……可以說，在數學學習中，整體思維是學生應該具備的一種最基本的思維。

二、整體思維的主要表現形式

整體思維在小學的主要表現形式有：整體代入、整體替換、整體配對、整體聯想等。

（一）整體代入，簡化計算

整體代入法：在解決問題時，將題目中的已知條件或者一些式子重新組合看做一個“整體”，并把這個“整體”直接代入其他式子，從而方便解題，簡化計算，避免運算的繁瑣和困難。

【例1】□+△=9，□+△+△+△=17，那么□=（? ），△=（? ? ）。

分析：仔細觀察這兩個式子，若要從已知條件直接求出□和△的值，雖然可以，從1+8=9、2+7=9、3+6=9、4+5=9，把這些數一一對應，直到算出結果，可以算出但會有點煩，而細心的同學可以發現，如果把□+△=9看作一個整體，再整體代入后一個式子，得到9+△+△=17，得出兩個三角形的和是8，一個三角形就是4，再次帶回第一個式子，可以得出正方形是5，從而得出答案。

（二）整體替換，轉換思維

整體替換法：在解決數學問題時，我們可以將題目中某個式子或者部分，用其他形式來表示，替換掉原來的式子或部分，轉換思維，更方便解決問題。

【例2】學校買來5個足球和10個籃球，共計550元。每個足球比籃球便宜10元，每個足球多少元？籃球呢？

分析：這是一道很簡單但也很典型的整體替換。由已知條件，我們可以把籃球全部替換成足球，或者把足球全部替換成籃球。假設買的全部是籃球，一共買了15個籃球，5個足球替換成5個籃球，需要補50元，那么15個籃球一共550+50=600（元），那么每個籃球價格：600÷15=40（元），每個足球價格：40-10=30（元）。足球與籃球的互相替換，成功解決了問題，將難題簡單化。

【例3】一個籠子可以容納18只同樣大小的鵝和9只同樣大小的鴨，或者容納14只同樣大小的鵝和15只同樣大小的鴨。如果這個籠子專門用來裝鵝，最多可以裝幾只鵝？

分析：此題如果直接去求解，因為沒有給出鵝和鴨的關系，會不知道怎么去求解。但如果我們能把兩個條件中鵝和鴨的關系看成一個整體，即：18只鵝的體重+9只鴨的體重=14只鵝的體重+15只鴨的體重，兩邊減去同樣的14只鵝的體重和9只鴨的體重，那就可以求出4只鵝的體重=6只鴨的體重，兩邊同時減半，2只鵝的體重=3只鴨的體重，這時候問題就明了了，將鴨轉換為鵝，9里面有3個3，而3只鴨等于2只鵝，所以9只鴨的體重等于6只鵝的體重，整體替換回到第一個條件，18+6=24（只），所以最多可以裝24只鵝。整體替換，將鴨與鵝互相轉換，使題目簡單明了。

（三）整體配對，尋找規律

整體配對法：在解決一些排列有規律的式子時，我們可以首尾配對，或者交叉配對等，構成一個新的整體，尋找并發現規律，簡便題目的運算，從而求出結果。

【例4】1+2+3+4+……+100

分析：這是著名的數學家高斯，7歲時解決的題目。剛看題目，不知道如何下手，但仔細觀察，可以發現題目的首尾是很有規律，且首尾項的和均為101，1+100=101，2+99=101……50+51=101。進而我們可以嘗試整體配對的方法，通過找出首尾項的規律，從而首尾配對求和，從1加到100有50組這樣的數，所以50×101=5050。

【例5】1+2-3+4+5-6+……+58+59-60+61+62

分析：看到這個題目時，我們首先從整體著眼，可以發現所求式子很有規律，兩個“+”，一個“-”，那我們可以3個數配對，也就是

1+2-3+4+5-6+……+58+59-60+61+62

=（1+2-3）+（4+5-6）+（7+8-9）+……+（58+59-60）+61+62

=0+3+6+……+57+61+62

=（0+57）×20÷2+61+62

=570+61+62

=693

（四）整體聯想，猜測論證

整體聯想法，在解題時尋求不同知識體系的內在聯系，從分析問題的整體結構出發，大膽的猜想，進而論證猜測，從而使問題的解決變得有據可循。

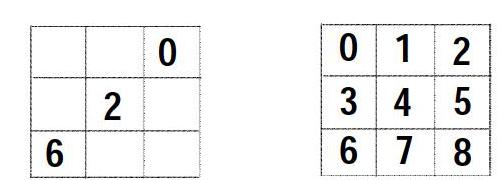
【例6】3×3的方格中，分別寫有0-8的數字，豎著讀時看做是由這三個數字組成的整數，橫著讀時，也看做是由這三個數字組成的整數，如下圖：豎著讀時，3個數分別是：36、147、258

橫著讀時，3個數分別是：12、345、678

現在，請在左邊的方格中寫入0-8這9個數字，其中0、2、6已經填入方格中，使豎著讀和橫著讀時的三個數的和相等。

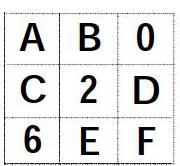
分析：依據常規，學生拿到題目肯定會覺得不知道怎么做，需要學生先理解、再思考，一個個試肯定不可以，這時候學生應該學會觀察思考，整體聯想，去猜測。為了方便，先在右圖中用字母表示空格。

這時候橫著讀為：AB0、C2D、6EF;豎著讀為：AC6、B2E、DF。其中A和F分別在百位和個位，不影響和的大小，可以不分析。整體聯想AB0+C2D+6EF=AC6+B2E+DF，只看百位A+C+6=A+B，合理猜測（1）C+6=B（2）C+6比B多1（3）C+6比B小1，有了合理的猜想，接下來一一驗證就可以。

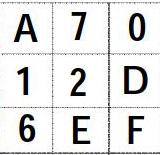
第一種情況只有C=1，B=7，此時表格如右圖，看十位7+2+E得數肯定大于10，相應的1+2+D也要大于10，D只能為8，而E=2與已知矛盾。

第二種情況C+6比B多1，則C=3，B=8，如左圖。此時十位上8+2+E=3+2+D，由于8+2=10，與假設的不進位矛盾，所以不成立。

第三種情況C+6比B小1。C=1，B=8。此時觀察十位，只能D=3，E=7。

這時只有4、5，任意帶入發現都可以。480+123+675=416

+827+35=1278

580+123+674=516+827+34=1377

在小學數學的教學中，我們必須注重對學生整體思維的培養，這樣不僅可以幫助學生解決數學題目，更能夠培養學生在生活中，樹立整體的思維，用全面的辯證的眼光去看待和解決問題。因此，整體思維的培養，在小學數學課堂是極其重要的。

【參考文獻】

[1]楊斌.小學數學思維能力的培養方法[J].教師博覽（科研版），2016（8）

[2]張曉明.數學思維在小學教學中的體現及探析[J].中文信息，2018（2）

[3]李青云.淺析韋特海默的數學教育思想在小學數學教學中的應用[J].新教育時代電子雜志（學生版），2018（24）

（淮安工業園區實驗學校，江蘇? 淮安? 223008）