Volterra型算子在Hardy空間和Bergman空間上的嚴格奇異性

林慶澤

（廣東工業大學應用數學學院，廣東 廣州 510520）

0 引 言

用H（Δ）表示復平面單位圓盤Δ 上所有解析函數f 組成的函數空間，則Hardy 空間H2的定義如下：

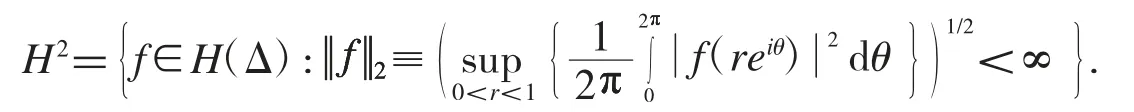
用 A2表示 Δ 上滿足

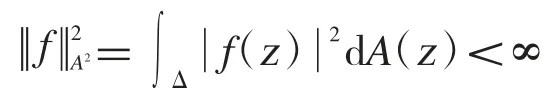
對于任一g∈H（Δ），定義Volterra 型算子Sg如下：

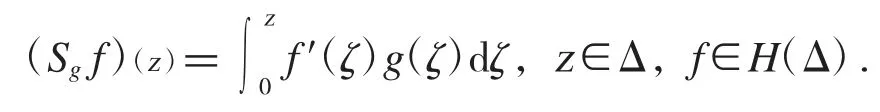
與Sg相伴而生的另一個算子是：

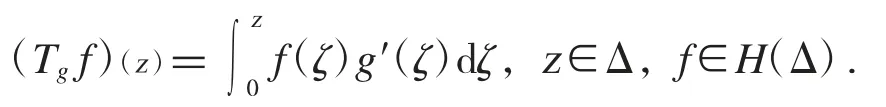
Pommerenke[1]首次研究Tg算子在Hardy 空間H2上的有界性并刻畫了其與BMOA 函數的指數之間的聯系.而關于Tg算子在一般的Hardy 空間Hp、Bergman Ap空間（0＜p＜∞）以及其它一些空間（包括加權Dirichlet 空間和加權Banach 空間等）上的有界性和緊性的刻畫可參考文獻[2-9].近年來，Miihkinen 等人[10-11]證明了Tg算子在Hardy 空間上的緊性與其嚴格奇異性的等價關系，其證明思路來源于文獻[12].本文首先給出Sg算子在Hardy空間H2以及Bergman 空間A2上的有界性和緊性的充要條件，接著給出了Sg算子在這些空間上的嚴格奇異性的刻畫，從而證明了該算子的緊性與其嚴格奇異性的等價關系.

1 Sg算子在Hardy 空間H2和Bergman空間A2上的有界性和緊性

我們首先給出Sg算子在Hardy 空間H2上的有界性和緊性的充要條件的完整刻畫.記H∞為Δ 上所有有界解析函數f 組成的函數空間.根據Littlewood-Paley 不等式[13]，Hardy 空間H2有一個等價范數：

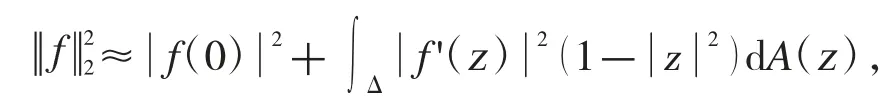
定理1若g∈H（Δ），則Sg算子在Hardy 空間H2上是有界的當且僅當g∈H∞.

證明若g∈H∞，則由Sg算子的定義可知，Sg算子在Hardy 空間H2上是有界的.

反過來，假設Sg算子在Hardy 空間H2上是有界的.由上面的Hardy 空間H2的等價范數可知，Sg算子在Hardy 空間H2上是有界的當且僅當存在C＞0 使得下面的不等式成立：

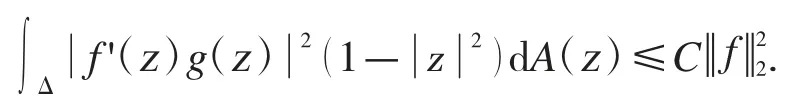
而根據文獻[14]中的定理3.1，這個不等式成立當且僅當測度是一個3-Carleson 測度，根據文獻[15]中關于Carleson 測度的等價條件的刻畫，有下面的不等式成立：

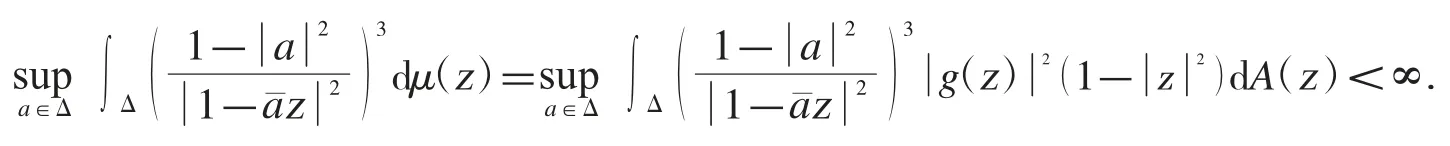
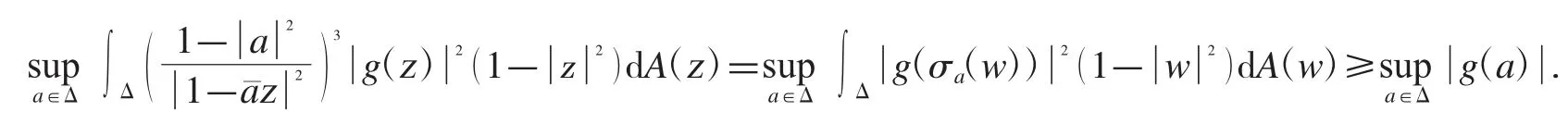
因此，g∈H∞.證畢.

定理2若g∈H（Δ），則Sg算子在Hardy 空間H2上是緊的當且僅當g≡0.

證明若g≡0，則很明顯，Sg算子在Hardy 空間H2上是緊的.反過來，假設Sg算子在Hardy 空間H2上是緊的.同樣根據文獻[14]可知，Sg算子在Hardy 空間 H2上是緊的當且僅當測度是一個緊的3-Carleson 測度，也就是等于下面的極限[14]成立：

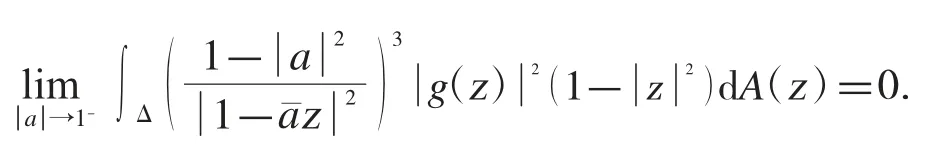
現在考慮Sg算子在Bergman 空間A2上的有界性和緊性條件.

定理3若g∈H（Δ），則Sg算子在Bergman 空間A2上是有界的當且僅當g∈H∞.

證明由于A2在范數意義上等價于加權Dirichlet 空間（參看文獻[8]），因此 Sg算子在Bergman 空間 A2上是有界的當且僅當乘法算子（（Mgf）（z）＝g（z）f（z））在加權Bergman空間上是有界的[16-17]，而這又等價于g∈H∞.證畢.

定理4若g∈H（Δ），則Sg算子在Bergman 空間A2上是緊的當且僅當g≡0.

證明由與定理3 的證明思路一樣.證畢.

2 Sg算子在Hardy 空間H2和Bergman空間A2上的嚴格奇異性

如果一個有界線性算子S:X→Y（其中X 和Y 是Banach 空間）限制在X 的任何一個無窮維閉子空間E 上所誘導出的線性算子SE:E→S（E）都不可能是同構映射，則稱算子S:X→Y 為嚴格奇異的.類似地，如果一個有界線性算子S:X→Y（其中X 和Y 是Banach空間）限制在X 的任何一個同構于l2空間的無窮維閉子空間E 上所誘導出的線性算子SE:E→S（E）都不可能是同構映射，則稱算子S:X→Y 為l2-奇異的[10-12].一個有界線性算子是緊的則必為嚴格奇異的，亦必為l2-奇異的；反之不然[12].

定理5若有界算子Sg在Hardy 空間H2上不是緊的，則Sg在Hardy 空間H2上不是l2-奇異的且Sg在Hardy 空間H2上不是嚴格奇異的.

換言之，定理5 是說，有界算子Sg在Hardy 空間H2上的緊性與其嚴格奇異性是等價的.

在證明定理5 之前，我們需要證明一個引理.由定理2 的證明可知，若Sg在Hardy空間H2上不是緊的，則存在Δ 內趨向于邊界（不妨假定為1）的序列使得

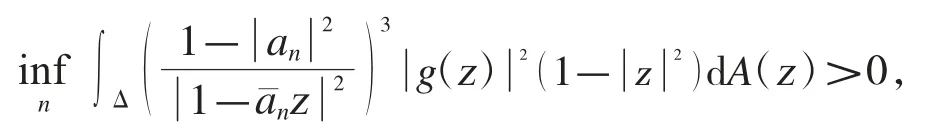
也就是，存在k＞0 使得對于所有的an，都有其中容易驗證，對于所有的

引理1若g∈H∞，對于Δ內趨向于1 的序列以及給定的ε＞0，定義集合記 m 為 Δ 的邊界 ?Δ的正則 Lebesgue 測度，則

證明（1）首先由幾何關系，存在δ＞0 使得對于所有的n、0≤r≤1 以及都有不等式成立從而，

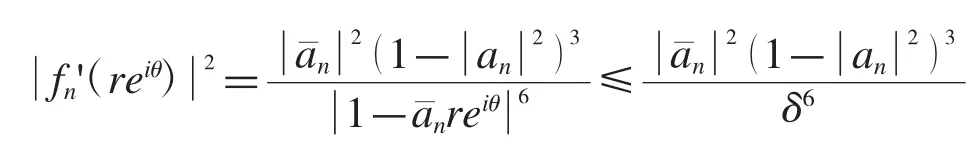
因此，對于任意的ζ∈?ΔAε，都有

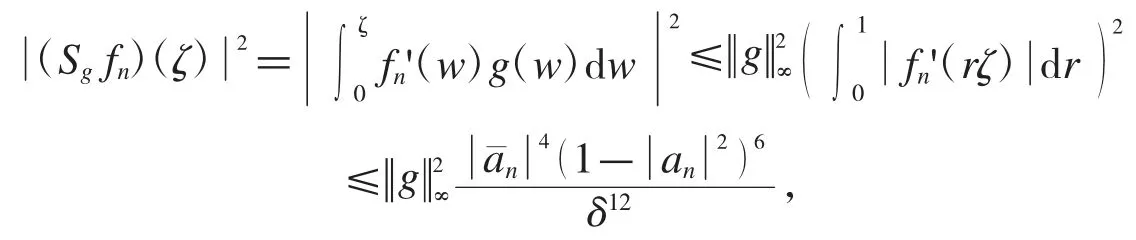
從而，

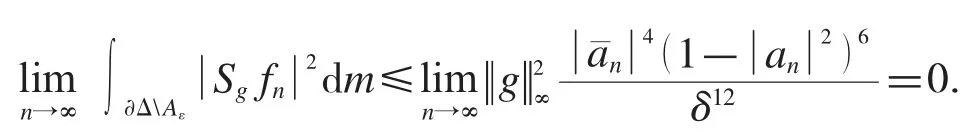
（2）當 ε →0 時，m（Aε）→0.由于 g∈H∞，算子 Sg是有界的，因此根據 Lebesgue 測度的絕對連續性，對于給定的證畢.

定理5 的證明 首先存在k＞0 使得對于所有的an，都有再由引理1，我們可以用歸納法得到，對于給定的序列ε1＞ε2＞…＞εn＞…＞0，我們能夠找到序列的一個子序列使得下面三個不等式成立：

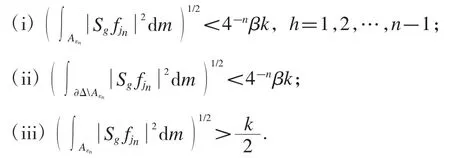
其中β 是一個充分小的正常數（其大小將在后面的證明過程中決定）.

接下來的按照文獻[12]的617-618 頁，我們得到，存在常數C1，C2＞0 使得對于任意的（bn）∈l2，都有若取g≡1，則可以推出存在常數C3，C4＞0 使得因此

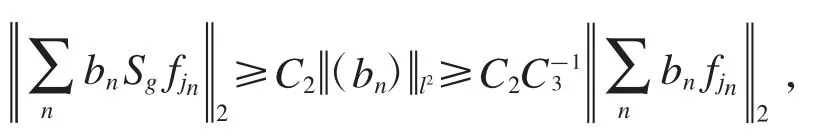
也就是，Sg在Hardy 空間H2上不是l2-奇異的，從而Sg在Hardy 空間H2上不是嚴格奇異的.因此，有界算子Sg的緊性與其嚴格奇異性是等價的.證畢.

定理6有界算子Sg在Bergman 空間A2上的緊性、l2-奇異性以及嚴格奇異性是兩兩相互等價的.

證明這是因為A2≈l2，可參照文獻[12]的625 頁.證畢.