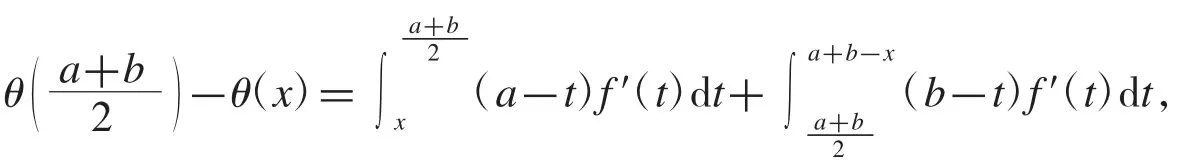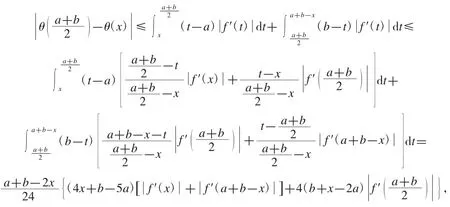Hermite-Hadamard不等式差值估計的一種推廣
時統業,曾志紅
(1.海軍指揮學院,江蘇 南京 211800;2.廣東第二師范學院學報編輯部,廣東 廣州 510303)
0 引 言
對于[a,b]上的凸函數f,成立
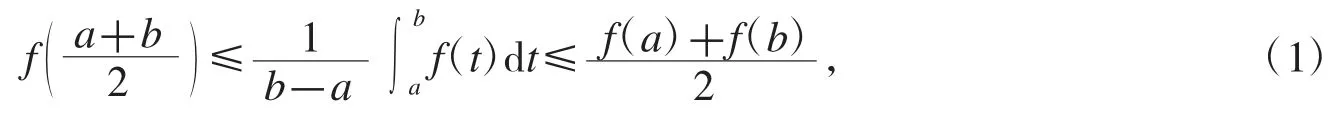
式(1)稱為Hermite-Hadamard 不等式.利用由式(1)生成的差值函數的單調性和凸性,可以加細式(1)[1-2].
利用導函數可以估計對由式(1)生成的差值[3-11].
設f 是定義在[a,b]上的函數,考慮定義在[a,b]上的函數
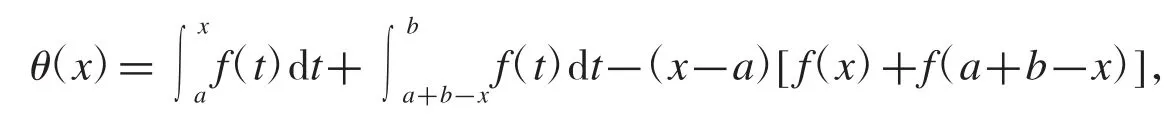
定義1[12-14]設函數f 定義在[a,b]上,如果存在常數M,對任意x,y∈[a,b]有則稱 f 在[a,b]上滿足 M-Lipschiz 條件,或者稱 f 是[a,b]上的M-Lipschiz 函數.
本文將給出與θ(x)有關的不等式,在特殊情況下得到已有文獻的結果.
1 主要結果
定理 1設 f 是[a,b]上的凸函數,則 θ(x)在上單調增加,從而對任意有
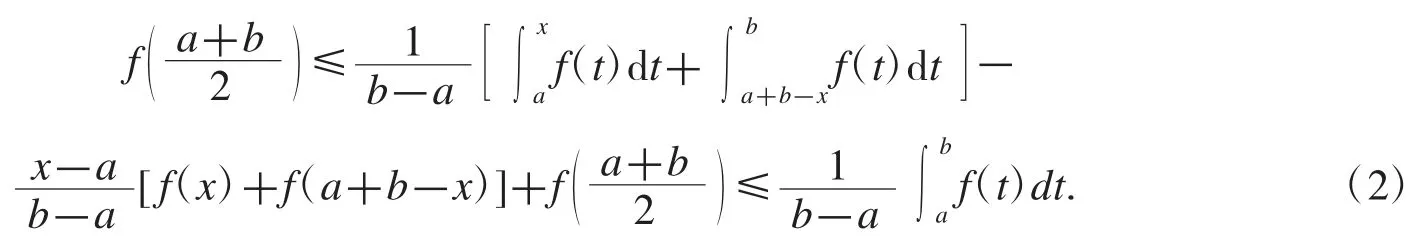
證明θ(x)在上連續,且對任意有故 θ(x)在上單調增加.從而對任意有即式(2)成立.
推論1設f 是[a,b]上的凸函數,則有
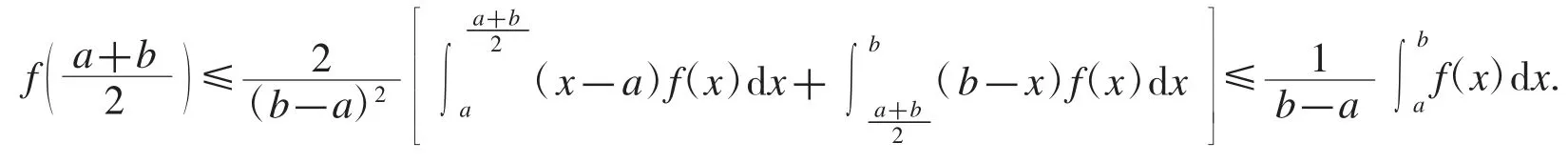
證明在式(2)中對x 在上積分即可得證.
定理2設f 是[a,b]上的可微函數,且f′在[a,b]上滿足M-Lipschiz 條件,則對任意有
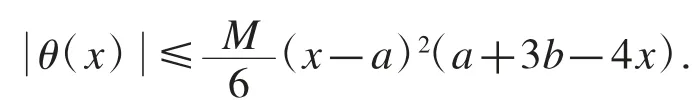
證明用分部積分法得
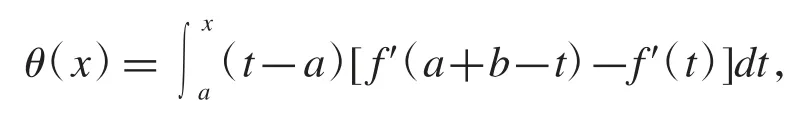
因f′在[a,b]上滿足 M-Lipschiz 條件,故有
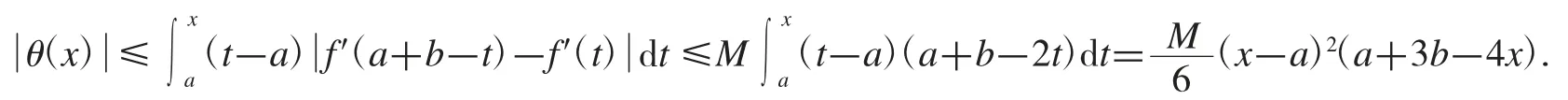
推論2設f 是[a,b]上的可微函數,且f′在[a,b]上滿足M-Lipschiz 條件,則有
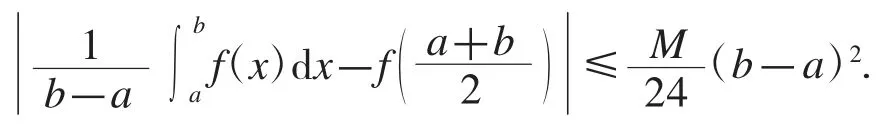
定理3設f 是[a,b]上的可微函數,且存在常數γ 和Γ,使得γ≤f′≤Γ,則對任意x∈[a,b],有
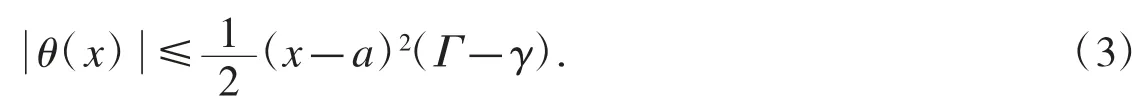
證明當 x=a 時,式(3)顯然成立.當 x∈(a,b]時,對函數 θ(t)和(t-a)2在[a,x]上使用Cauchy 微分中值定理,存在ξ∈(a,x),使得
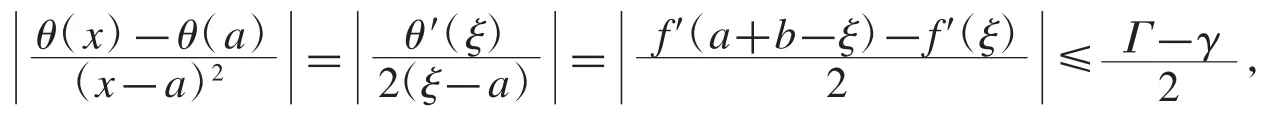
故式(3)成立.
推論3設f 是[a,b]上的可微函數,且存在常數γ 和Γ,使得γ≤f′≤Γ,則有

定理4設f 是[a,b]上的凸函數,且存在,則對任意x∈[a,b]有
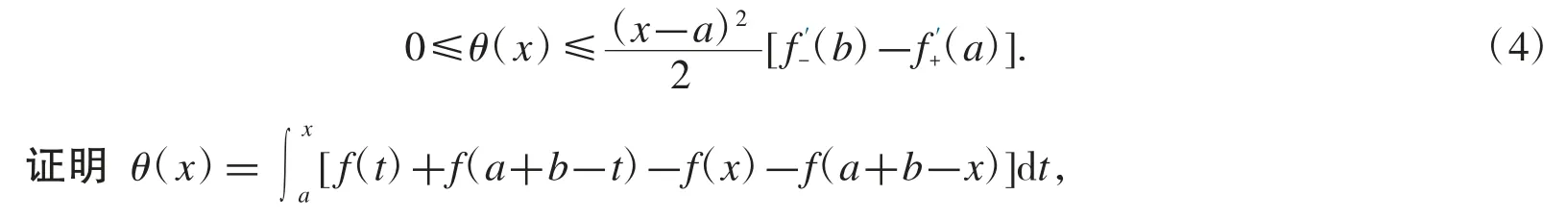
對任意 t∈[a,x],有
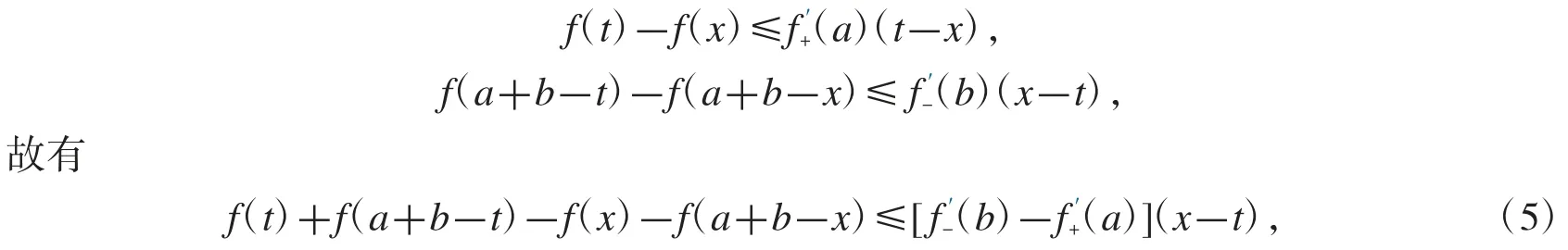
在式(5)中對 t 在[a,x]上積分,則式(4)得證.
推論4[7]設f 是[a,b]上的凸函數,且存在,則有
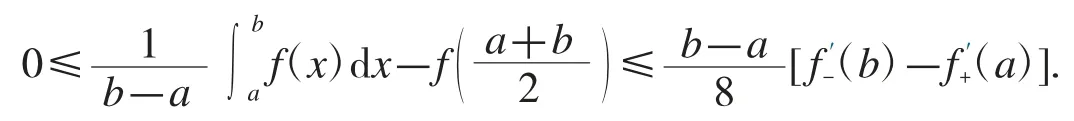
定理5設f 是[a,b]上的二階可微函數,且存在常數m 和M,使得m≤f″≤M,則
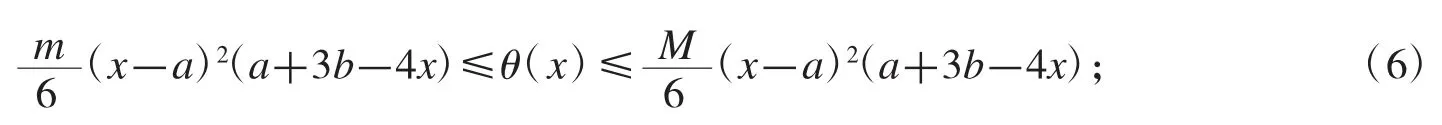

證明(i)因為m≤f″≤M,故對任意有
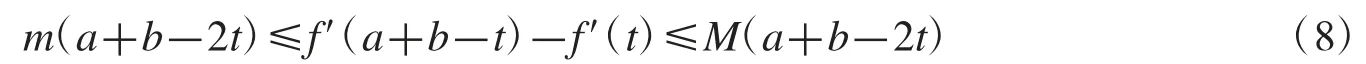
將式(8)乘以(t-a),然后對 t 在[a,x]上積分,則式(6)得證.
(ii)對任意 t∈[a,x),t≠a+b-x,設
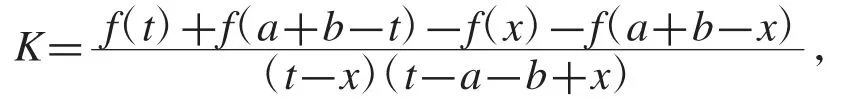
考慮函數
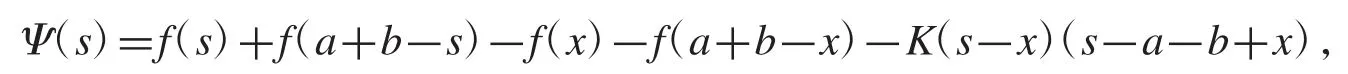
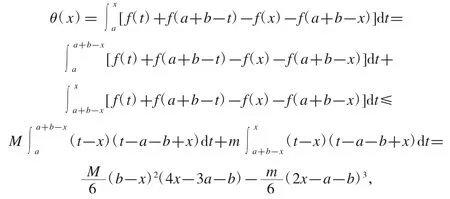
即式(7)的右邊部分得證.類似可證式(7)的左邊部分.
推論5[5-6]設f 是[a,b]上的二階可微函數,且存在常數m 和M,使得m≤f″≤M,則有
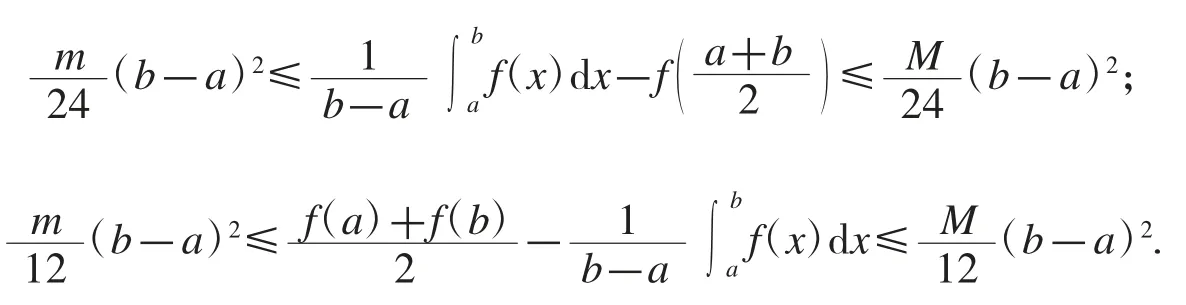
定理6設f 是[a,b]上的可微函數,且存在常數m 和M,使得γ≤f′≤Γ,則對任意有
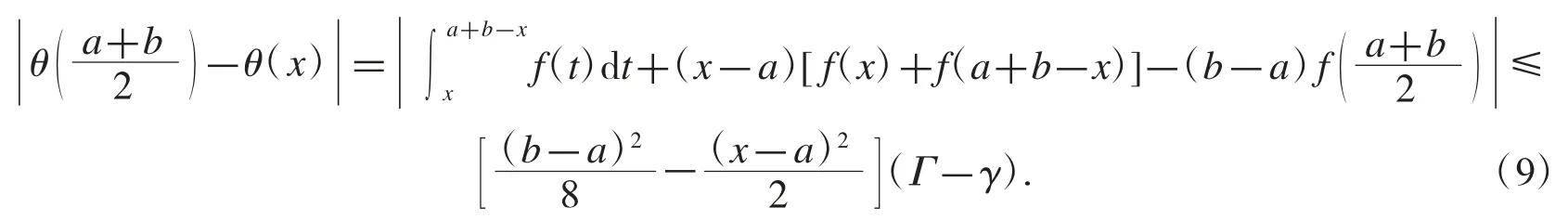
證明當時,式(9)顯然成立.當時,對函數 θ(t)和在上使用Cauchy 微分中值定理,存在使得
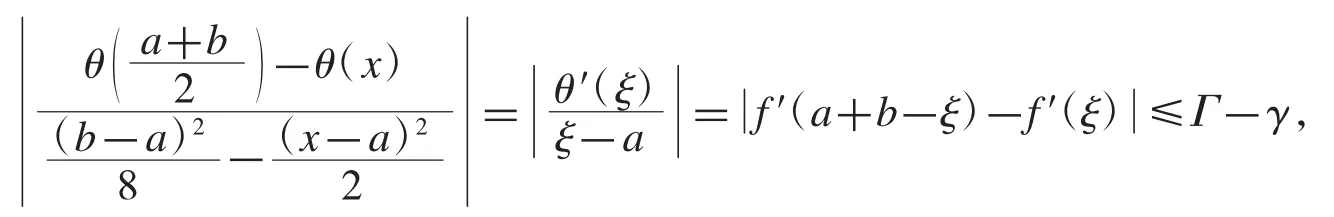
故式(9)成立.
定理7設f 是[a,b]上的凸函數,且存在,則對任意有
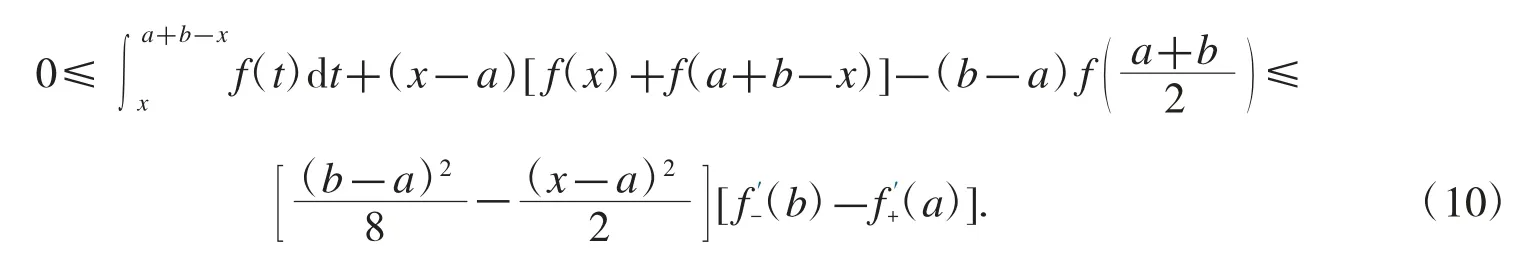
證明注意到
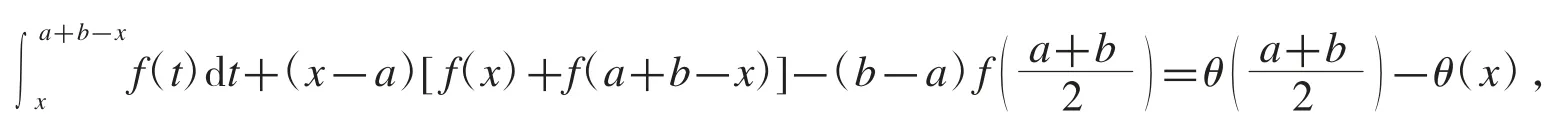
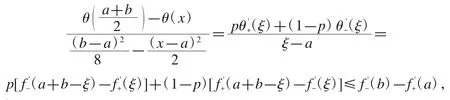
故式(10)成立.
定理8設f 是[a,b]上的可微函數,且f′在[a,b]上滿足
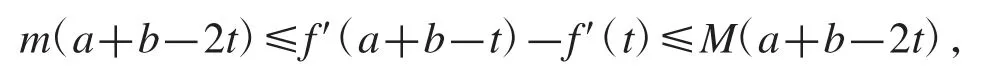
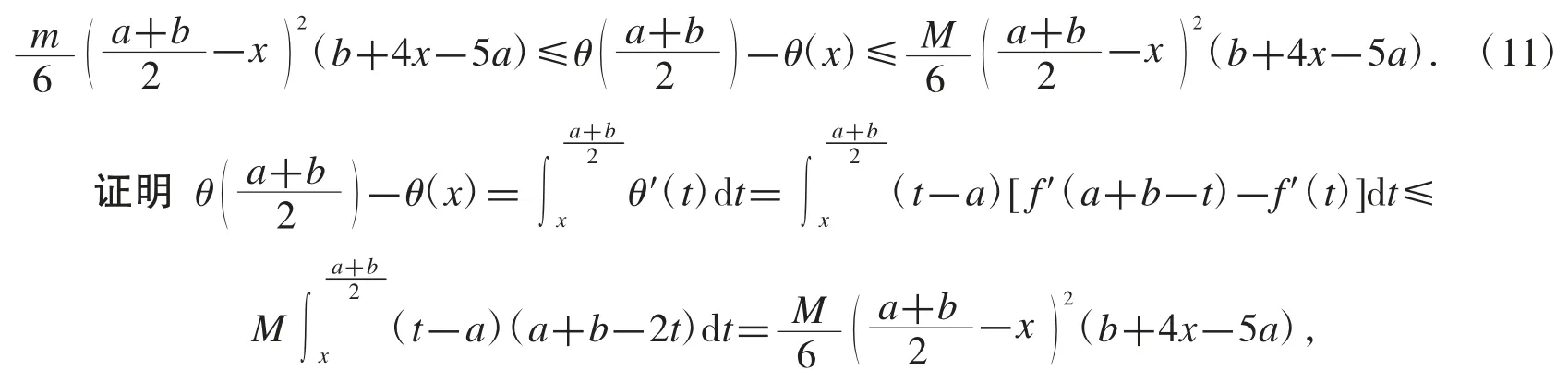
式(11)的右邊部分得證,類似可證式(11)的左邊部分.
推論6設f 是[a,b]上的可微函數,且存在常數m 和M,使得m≤f″≤M,則對任意由式(11)成立.
定理9設f 是[a,b]上的可微函數,且是[a,b]上的凸函數,則對任意有
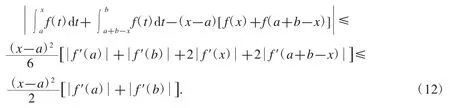
證明用分部積分法得

推論7[3]設f 是[a,b]上的可微函數,且是[a,b]上的凸函數,則有
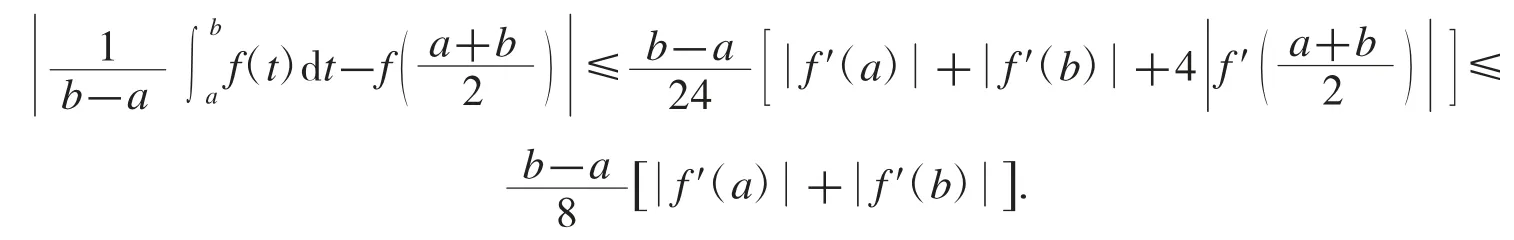
定理10設f 是[a,b]上的可微函數,且是[a,b]上的凸函數,則對任意有
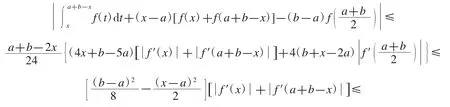
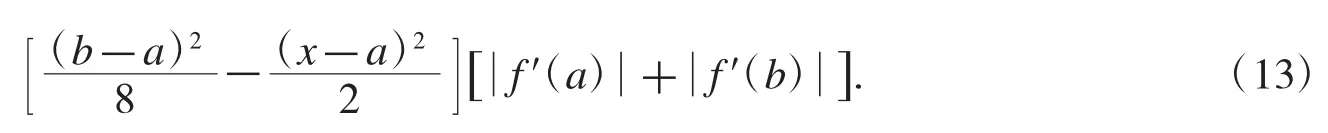
證明用分部積分法得