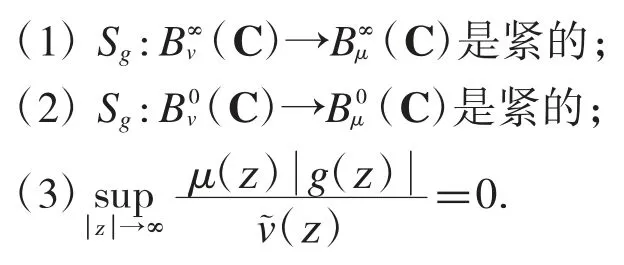復平面加權Banach空間及Bloch型空間上的Volterra型算子
林慶澤
(廣東工業大學應用數學學院,廣東 廣州 510520)
0 引 言
用H(C)表示復平面C 上所有整函數(entire function)組成的函數空間,
對于任一g∈H(C),定義Volterra 型算子Sg如下:

與Sg相伴而生的另一個算子是:
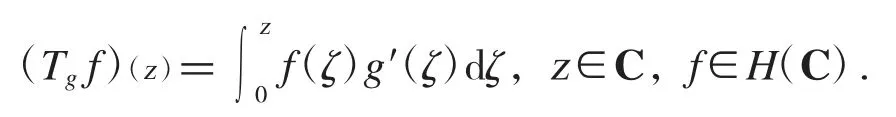
在復平面單位圓盤上,Pommerenke[1]首次研究Tg算子在Hardy 空間H2上的有界性,并刻畫了其與BMOA 函數的指數之間的聯系.而關于Tg算子以及Sg算子在一般的Hardy空間Hp(0<p<∞)、Bergman 空間Ap(0<p<∞)以及其它一些空間(包括加權Dirichlet空間等)上的有界性和緊性的刻畫可參考文獻[2-8].而在整個復平面上,Constantin 在文獻[9]中首次研究了Tg算子在Fock 空間上的有界性和緊性.接著,Constantin 和Pelaez在文獻[10]中研究Tg算子在更一般的加權Fock 空間上的有界性和緊性等問題.
Lin 最近在文獻[11,18]中刻畫了Tg算子以及Sg算子在復平面單位圓盤上的加權Banach 空間以及Bloch 型空間上的有界性及緊性,推廣了Smith 等人在文獻[12]中的成果.Bonet 和Taskinen 在文獻[13]中研究了Tg算子在復平面上加權Banach 空間上的有界性和緊性問題,本文研究Sg算子在復平面上加權Banach 空間以及Bloch 型空間上的有界性和緊性問題,給出其充要性的刻畫.
1 預備知識
定義1如果函數v(r):[0,+∞)→(0,+∞)是單調遞減的且滿足對于任意的正整數N,都有則稱函數 v(r)為權函數.對于復數z,定義
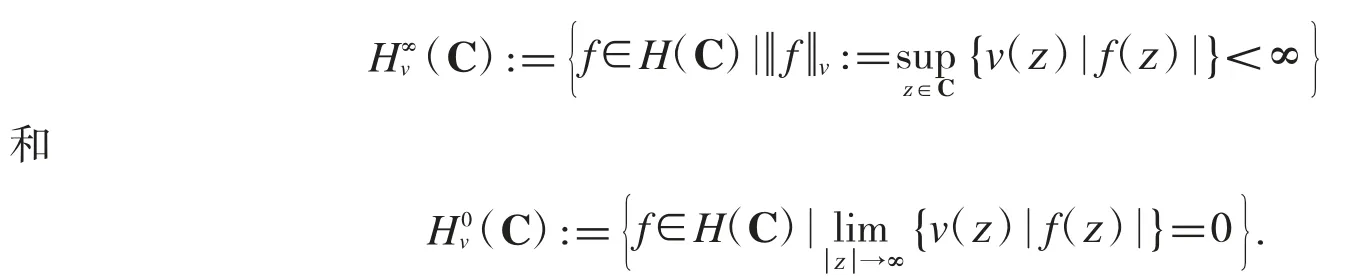

定義2權函數v 的關聯權(associated weight)的定義如下:
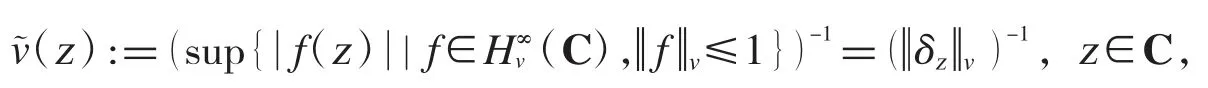
其中δz表示點z的點估值泛函.
定義3權函數v 是本性的(essential)的,如果存在C>0 使得對于任意的z∈C,都有
一個權v 是本性的當且僅當存在C>0 使得對于任意的z0∈C,存在向量使得
受文獻[11,15]的啟發,我們將Sg算子在復平面上加權Banach 空間以及Bloch 型空間上的有界性和緊性問題轉化為乘法算子
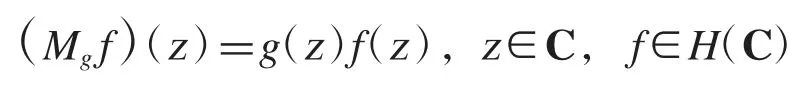
在對應的復平面上加權Banach 空間的有界性和緊性問題.下面兩個引理給出了乘法算子Mg在復平面上加權Banach 空間之間的有界性和緊性的刻畫.
引理1[13]若v 和μ 都為權函數,則對于給定的g∈H(C),以下條件相互等價:

引理2[13]若v 和μ 都為權函數,則對于給定的g∈H(C),以下條件相互等價:
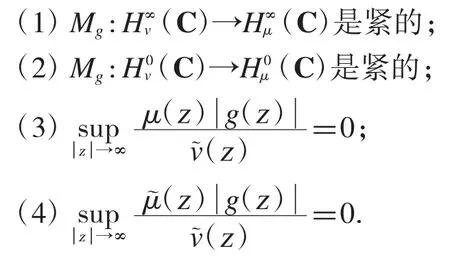
2 Volterra型算子Sg的有界性及緊性
在這一節里,我們將刻畫Volterra 型算子Sg在復平面上加權Banach 空間以及Bloch 型空間上的有界性和緊性的充要條件.
定理 1令 μ1和 μ2都為權函數,且存在 rφj>0 使得 φj:=1/μj在[rφj,∞)上屬于 C2類,其中j=1,2.令φ'(rφj)>0 且φj'在[rφj,∞)是單調遞增的并滿足:對于任意正整數n,都有若 μ1是本性的,則對于給定的g∈H(C),以下條件相互等價:
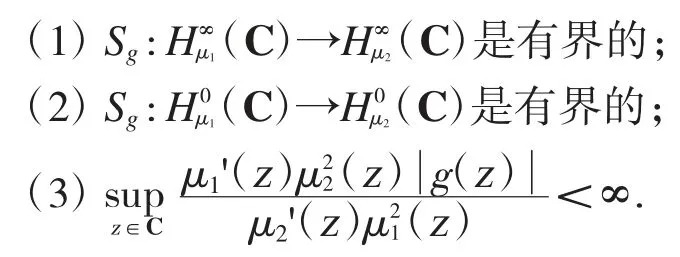
證明記
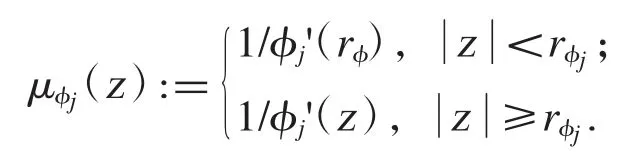
則μφj也是權函數.由文獻[13]的命題3.1 及命題3.2 可知,在定理1 所給定的條件下,積 分算子以及微分算子都是有界的.同樣地,積 分 算 子以及微分算子都是有界的.由于有關系式 Sg=TzMgDz以及 Mg=DzSgTz,故是有界的當且僅當是有界的,同樣地,是有界的當且僅當是有界的.而由于μ1是本性的,根據引理1,是有界的當且僅當是有界的,當且僅當也就是當且僅當證畢.
類似于定理1 的證明過程,我們可以得到下面幾個定理.
定理 2令 μ1和 μ2都為權函數,且存在 rφj>0 使得 φj:=1/μj在[rφj,∞)上屬于 C2類,其中j=1,2.令φ'(rφj)>0 且φj'在[rφj,∞)是單調遞增的并滿足:對于任意正整數n,都有若 μ1是本性的,則對于給定的g∈H(C),以下條件相互等價:
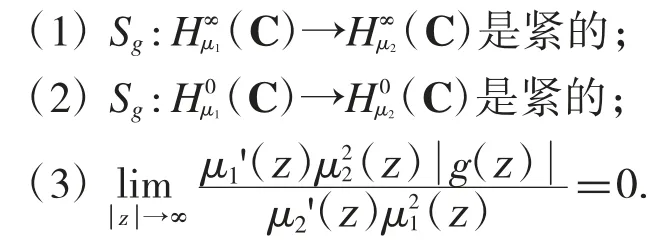
定理3若v 和μ 都為權函數,則對于給定的g∈H(C),以下條件相互等價:
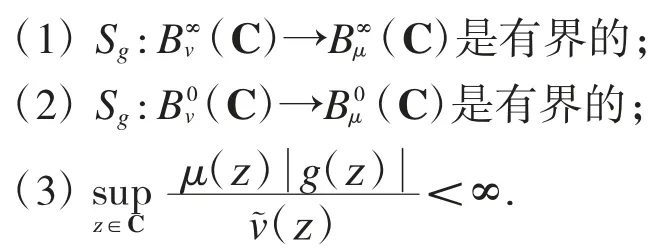
定理4 若v 和μ 都為權函數,則對于給定的g∈H(C),以下條件相互等價: