智能RGV的動態調度策略

杜一婷，馮夢若，李佳軍，方 睿

（汕頭大學數學系，廣東 汕頭 515063）

0 引 言

智能軌道式自動引導車（Rail Guide Vehicle，RGV）是現代自動化生產車間中的重要工具，其可連接不同數量，不同種類的計算機數控機床（Computer Number Controller，CNC）.隨著我國自動化行業的發展，智能RGV 逐漸應用到大物流的輸送、調度問題.同時，智能加工系統中存在機器故障等情況，會對RGV 動態調度提出挑戰.為提高物流系統效率，需要設置合理的“智能RGV 的動態調度策略”.本文根據2018 年全國大學生數學建模競賽B 題給定的智能加工系統作業情況以及作業參數，嘗試解決以下兩項任務：

任務1：對一般問題進行研究，給出RGV 動態調度模型和相應的求解算法；

任務2：利用表1 中系統作業參數的3 組數據分別檢驗模型的實用性和算法的有效性，給出RGV 的調度策略和系統的作業效率，并將具體的結果填入附件.

其中智能加工系統作業3 種具體情況為：

（1）一道工序的物料加工作業情況，每臺CNC 安裝同樣的刀具，物料可以在任一臺CNC 上加工完成；

（2）兩道工序的物料加工作業情況，每個物料的第一和第二道工序分別由兩臺不同的CNC 依次加工完成；

（3）CNC 在加工過程中可能發生故障的情況，人工處理，且故障的發生概率約為1%，每次故障排除時間介于10-20 min 之間，故障排除后即刻加入作業序列，未完成的物料報廢.分別考慮一、二兩道工序的物料加工作業情況.

注：題目、參數和附件可到全國大學生數學建模競賽官方網站http：//www.mcm.edu.cn 下載

1 模型的假設

為了方便研究，在不改變題目要求的前提下，我們對模型作以下假設：

（1）假設每臺RGV 每次清洗作業和上下料作業的時間相同；

（2）每臺CNC 的加工效率相同且保持穩定；

（3）假設RGV 先將生料放到CNC，完成上料工作后，再進行熟料的清洗工作；

（4）假設上下料傳送帶的連動或獨立運動對模型無影響；

（5）假設智能加工系統中的所有傳感器反應時間很短，可忽略不計.

2 任務1的模型建立與求解

2.1 任務1的分析

首先需要考慮一道工序的物料加工作業，且CNC 沒有故障的情況，設該情況為情況1.

2.1.1 情況1 分析

在此情況中，每個物料只有一道加工工序，所以每臺CNC 安裝同樣的刀具.此時，物料可以在任意一臺CNC 上加工完成，即8 個CNC 是通用并行機，可視為是性質相同的8 個固定點.每兩個不同點之間可以通過RGV 連接，為了提高調度效率，RGV 需要尋找最短路徑，所以該問題為最短路問題.

RGV 的路徑取決于RGV 和CNC 的狀態和位置，是動態的.所以可以用RGV 動態路徑的旅行時間代表其路徑長度，利用動態規劃的思想進行路徑選擇的決策，建立基于動態路徑的調度模型，并且利用MATLAB 編寫對應程序.

再者，我們需要考慮兩道工序的物料加工作業，此時，若仍不考慮CNC 出現故障的情況，設該情況對應情況2.若考慮CNC 在加工過程中可能發生故障，設該情況對應情況3.

2.1.2 情況2，3 分析

在情況2、3 中，每個物料需要兩道加工工序，所以不同CNC 可能安裝不同刀具.基于情況1 的分析，需要在動態規劃中加入與工序相關的約束條件，并且將其具體體現在算法中.此時的物料調度步驟增多，不僅需要考慮RGV、CNC 的狀態以及位置，而且需考慮安裝兩種刀片的CNC 各有多少個，以及不同類型的CNC 的排布.通過分析表1 中的數據可得，RGV 的運行時間相對CNC 加工時間很短，所以不同類型CNC 的數量對系統效率的影響要遠大于CNC 分布的影響.

2.2 模型建立

2.2.1 基于動態路徑的調度模型

基于情況1 的分析，RGV 的旅行路徑是動態的，為尋找最短路徑，需建立基于動態路徑的調度模式.

2.2.1.1 固定起點的最短路問題

應用到任務問題中，RGV 在固定8 個CNC 任務點之間尋找運動的最短路徑，且此過程在8 h 班次中，不斷重復迭代更新最短路徑，具有周期性.

RGV 在智能加工系統開始工作后，能在直線軌道上移動或停止等待；以兩臺相鄰CNC 的距離為1 個單位，RGV 可連續移動1 個單位、2 個單位和3 個單位.RGV 給兩臺CNC 放置生料的順序類型，可分為從奇數側到偶數側、奇數側到奇數側及偶數側到偶數側，如圖1 所示.

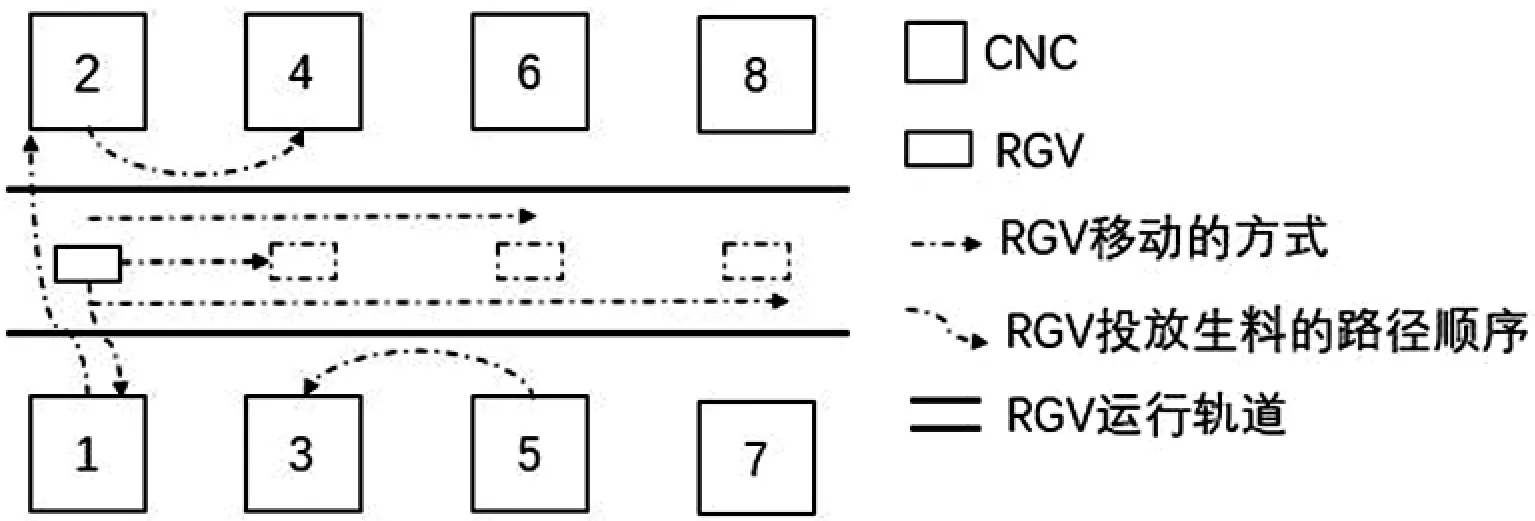
圖1 RGV 工作路徑的類型及物料需求點CNC

一般情況下，物料輸入智能加工系統的狀態服從均勻分布.設系統停止工作時，得到成料量為n，單位為一臺CNC 加工的量，對應加工物料的序號.在系統工作的過程中，RGV 的運輸要滿足8 臺CNC 的上料和下料的需求，因此，在存在服務質量和可行性約束且消耗最少的能量的情況下，RGV 的工作量為2n.

定義 P 為 RGV 上料，D 為 RGV 下料，其中 P＝{1，2，…，n}，D＝{n＋1，n＋2，…，2n}.當RGV 放置第i（1≤i≤n）個物料時，它與RGV 給CNC 進行第i＋n 個下料工作相關聯.此時RGV 的路徑問題，由一個有向的圖G＝（V，E）描述，V 中的頂點i 表示RGV 上料或下料工作的需求點，其中e＝（i，j）表示兩個工作之間的可能處理順序，即工作j 是否可以在工作i 之后立即處理.為保證系統作業的開始和結束，還增加了兩個虛擬的工作任務，分別為 0 和 2n＋1，表示 RGV 的起始位置和結束位置.因此定義 V′＝P∪D＝{1，2，…，2n}，則V＝{0}∪V′∪{2n＋1}，對應的i，j∈V，k＝1，2，…，2n＋1.

2.2.1.2 RGV 判斷過程

在假設條件的基礎下，RGV 動態調度需要在RGV 對某些時間狀態做出判斷后開始，判斷出到某臺CNC 進行工作的過程總時間最小，則到相應CNC 進行作業.RGV 判斷過程涉及的時間變量如表1 所示.

表1 RGV 判斷時間段

RGV 判斷后，要得到移動到哪一臺CNC 的時間最短，即最短路徑，然后再進行調度作業，不斷針對路徑進行循環判斷，直到智能加工系統工作時間結束.實際過程中可能存在的一種情況，如圖2 所示，即CNC4#的加工完成時間比CNC6#長，RGV 移動到CNC4#，但在去CNC4#的過程中，經過CNC6#之前，若此時CNC6#也給RGV 發出需求訊號.

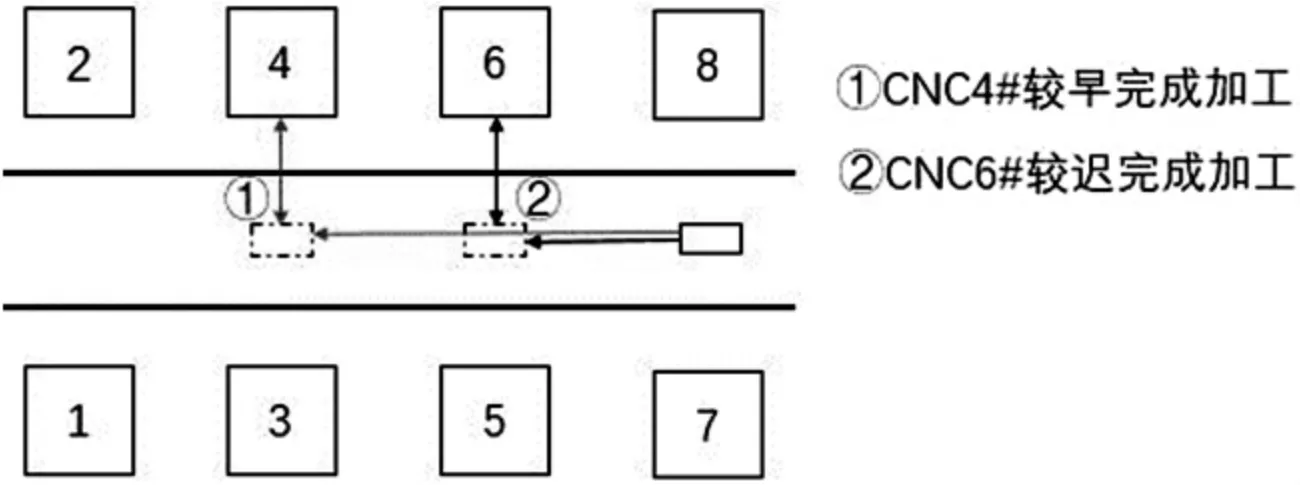
圖2 判斷的特殊情況

那么若此時依然移動到CNC4#，將會浪費時間資源，減少成料產出.所以RGV先決定給CNC6#作業，此外RGV 給不同編號的CNC 上下料的時間也不同，也會產生影響.因此，當設定RGV 決策時，要判斷三者之和的最小值，即

2.2.1.3 分治法確定成料產出量及上下料作業時間點

動態規劃基本上是一種完全枚舉算法，嘗試通過分治法以使需要進行的計算量最小化.這種方法在找到最終答案之前解決了一系列的子問題，并確定每一個子問題的最優解以及每個子問題對于最終目標問題的貢獻.在每一次迭代過程中，其所確定的子問題最優解均大于以往求解的子問題的解，從而為了求解當前的子問題，需使用求解以往所有子問題獲得的信息.

根據文獻[1]的研究結果，我們將每個迭代過程的最短時間分為5 個時間段，綜合判斷后得到一個迭代過程的最短時間，再迭代n 次，得到所用時間最短，成料產出最大的作業方案.

（1）初始狀態：T1＝0

（2）迭代方程：minTi＝Σ（Td＋Tl＋Tz）min＋Tj＋Tq，i＝1，2，…，n.

（3）最優值方程：ΣTi≤8×60×60.

系統的初始狀態：RGV 位于CNC1#、2#前，不論先為哪臺投放物料，初始時間總為0；每一次迭代過后，RGV 得到最短時間minTi，迭代n 次；由于系統一個班次的工作時間為8 h，而我們在建模過程中所用的時間單位為s，所以有最優值方程.

2.2.1.4 確定RGV 為CNC 加工的方向順序

根據文獻[2]的研究結果，我們可以結合有向圖G，給出設置RGV 路徑移動方向順序的模型.最優RGV 路徑問題的求解過程可以表述為下列公式中定義的混合整數規劃.此部分建立了一個RGV 最優路徑問題的數學模型.

主要參數和符號被定義如下：

P 是任務集，P＝{1，2，…，n}，n≤8；

D 是任務集，D＝{n＋1，n＋2，…，2n}；

V′＝P∪D，V＝{0}∪V′∪{2n＋1}；

ti表示 RGV 到上下料需求點的旅行時間，i∈V{2n＋1}，t0＝0；

Sij表示在上下料點i，j 之間的RGV 行駛距離；

Tij是在上下料點i，j 之間的RGV 行駛時間；

xij表示上下料需求i 是否在j 之前處理0，1 變量；

bi表示第i 個任務的初始時間；

wi表示RGV 完成某臺CNC 上料或下料后的負載物料單位，i∈P，w0＝0.

約束條件：

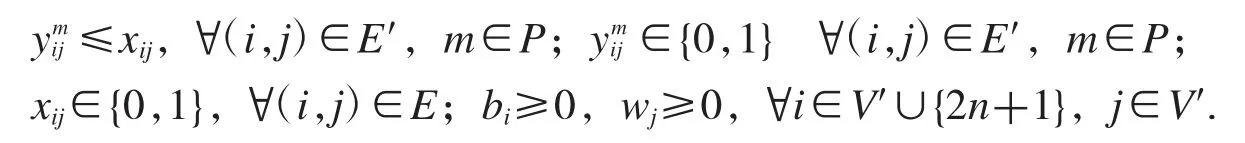
目標函數表示RGV 的總時間成本最小值，也是wi和xij的雙線性函數，RGV 最優路徑（i，j）∈E 與一個耗能成本cij（wij）及一段行駛時間Tij相關聯.RGV 負載的物料最多為3 個種類，即RGV 抓取的未加工的生料、從CNC 中取回的已加工的熟料和清洗后的成料.

當RGV 判斷出在當前位置沿路徑（i，j）移動到下一個CNC 進行作業的最優路徑時，我們可以利用牛頓法則，求得總時間成本cij（wij），即

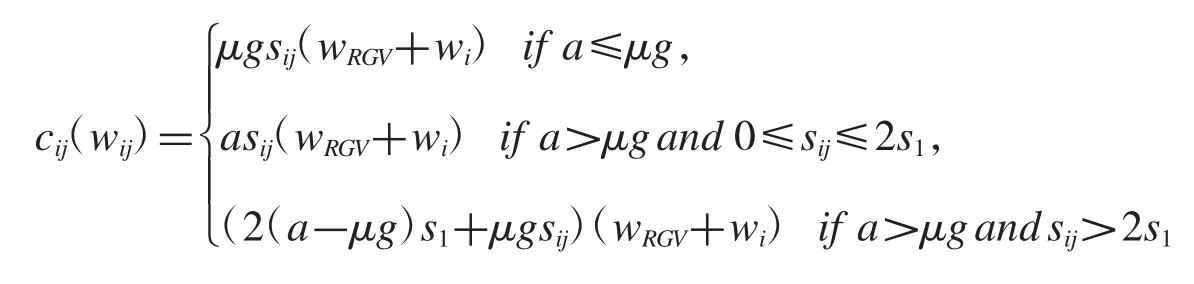
經過約束條件的篩選計算，得出一次循環中耗時耗能最小的路徑.

2.3 RGV實時路徑仿真算法

對于智能RGV 動態調度問題.存在許多智能高級算法，例如遺傳算法和模擬退火算法.但是對于這些算法，RGV 運動路徑隨機性太強，且算法中參數的設計很大程度上取決于經驗，準確率常常不夠高.對此我們選擇用MATLAB 軟件編寫符合實際的模擬仿真算法，提高算法對該問題的適用程度.

假設智能加工系統的運行狀態穩定且CNC 無故障，在此情況下得出物料最大產出以及最優路徑.為了能讓RGV 動態調度過程更切合實際生產過程，對RGV 設置滯留時間懲罰系數.

RGV 一共有四個位置可供選擇，{1，2，3，4}.每一個位置的操作對象只有兩個.令RGV 的位置為a，當a＝1 時，RGV 可以操作的對象為CNC1，CNC2；

當a＝2 時，RGV 可以操作的對象為CNC3，CNC4；

當a＝3 時，RGV 可以操作的對象為CNC5，CNC6；

當a＝4 時，RGV 可以操作的對象為CNC7，CNC8.

將RGV 位置以及操作對象作為變量，則一共有八種方案.可以考慮窮舉法.令操作對象為c，c 為八行一列的向量，c 中元素的值域取值為{0，1}，c 里面的元素最多有一個1.元素為1 的那一列的編號，代表的是RGV 操作對象的CNC 編號.例如c＝［0 1 0 0 0 0 0 0］，表示RGV 將要對CNC2 進行操作.綜上所述，RGV 位置以及操作對象，只有以下八種方案.

當 a＝1 時：c＝［1 0 0 0 0 0 0 0］或［0 1 0 0 0 0 0 0］

當 a＝2 時：c＝［0 0 1 0 0 0 0 0］或［0 0 0 1 0 0 0 0］

當 a＝3 時：c＝［0 0 0 0 1 0 0 0］或［0 0 0 0 0 1 0 0］

當 a＝4 時：c＝［0 0 0 0 0 0 1 0］或［0 0 0 0 0 0 0 1］

算法的主要參數和符號被定義并列在表2 中，以便于參考.算法步驟：

表2 算法中的變量與符號

Step1：RGV 判斷通過路徑所需的時間以及CNC 的工作狀態.首先，RGV 根據當前位置到下一個物料投放的每個CNC 之間的路徑距離長短和每一臺CNC 是否處于加工狀態，以確定通過路徑的最短時間.

Step2：每一次移動需要服從的調度要求：符合調度的要求：

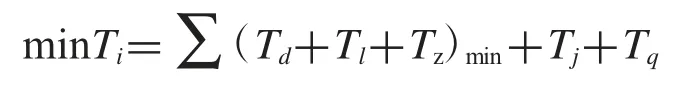
Step3：RGV 做出調度決策后，立即移動到下一個上下料需求點.

Step4：RGV 上下料操作完成前后記錄耗費的總時間，更新CNC 的狀態、物料的裝載、更新已使用的總時間ΣminTi.

Step5：循環條件ΣTi≤8×60×60；若總時間超過8 h，則停止循環，輸出物料最大產出以及最優路徑；反之，則繼續循環判斷，重復Step1-4.

2.4 基于空閑時間插入法的故障擾動模型

基于不考慮故障時的情況3，在生成預調度時，根據故障特征——以1%的幾率隨機產生，插入空閑時間——10 到20 min，故障間隔時間一般服從離散隨機分布，根據文獻[3]研究結果，設其為泊松分布：

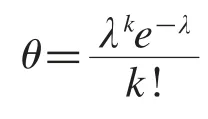
則加工工件n 時發生故障的概率為

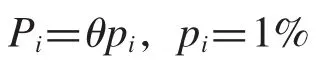
發生故障的工件n 需要插入的額外時間為

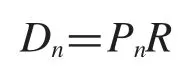
其中，

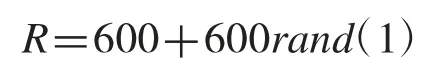
2.4.1 故障擾動下的RGV 動態調度算法

基于情況1，2 中的求解算法，該空閑時間插入的算法步驟為：

Step1：首先確定處于工作狀態的CNC，若CNC 處于工作狀態則進入Step2；

Step2：在“RGV 位置及狀態判斷”函數中考慮故障情況，從而影響可供RGV 決策集；

Step3：在迭代中對8 個CNC 設置故障擾動；

Step4：確定出現故障的CNC 編號；

Step5：將故障處理時間插入更新機制.

2.5 模型結果

2.5.1 一道工序的智能調度模型結果

一道工序的物料加工作業情況，每臺CNC 安裝同樣的刀具，物料可以在任一臺CNC 上加工完成.

我們建立的模型的動態調度模型基本適用于情況1，因此，基于動態路徑規劃及TSP 的動態調度模型，以及最短路徑算法，用已給數據設置對應的參數，用MATLAB編寫程序，得到RGV 為CNC 上下料作業的編號順序，即最優的動態路徑.運行結果顯示，對不同組數據的最優動態路徑相同，如圖3 所示.

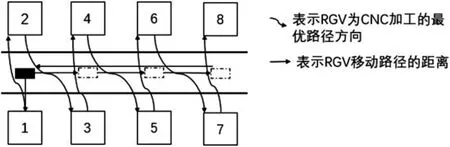
圖3 CNC 加工系統只有一道工序的最優路徑

即最優路徑是RGV 為CNC 進行上下料工作的編號先后順序為CNC#1、CNC#2、CNC#3、CNC#4、CNC#5、CNC#6、CNC#7、CNC#8.并且在此調度方案下每班次8 h結束時，得到最多的成料產出.分別給出3 組實驗中最優路徑循環的相關數據，如表3，4，5 所示.

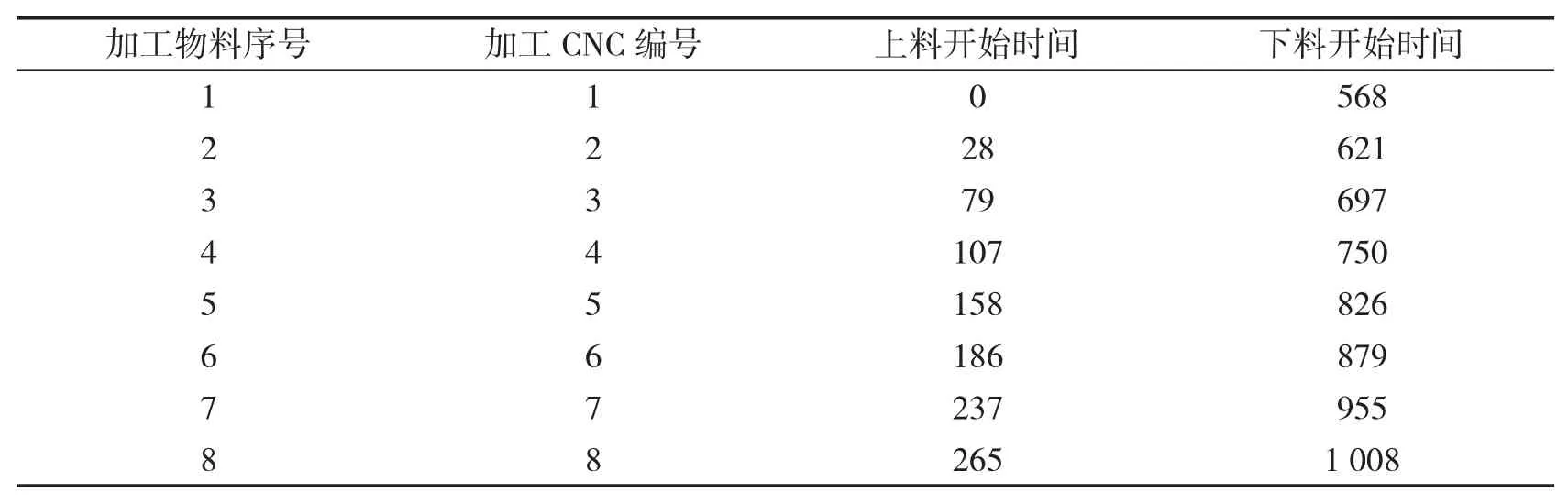
表3 第1 組數據：成料產出n＝365

表4 第2 組數據：成料產出n＝342

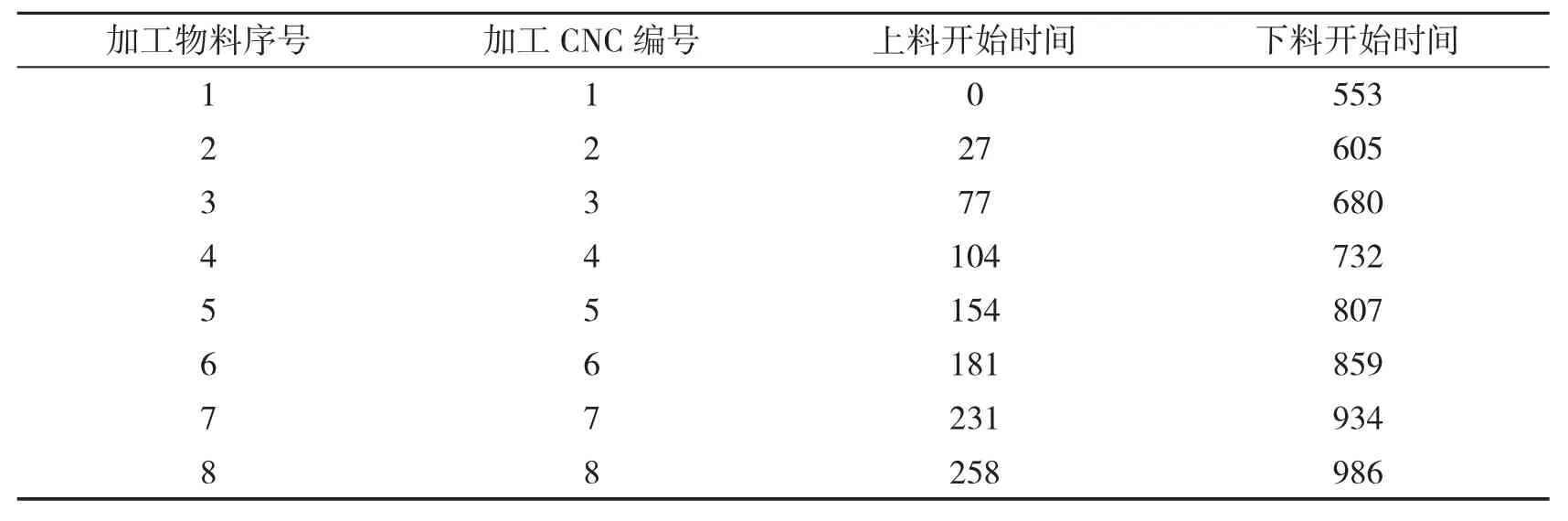
表5 第3 組數據：成料產出n＝375

2.5.2 兩道工序的智能調度模型的結果

針對兩道工序的物料加工作業情況，每個物料的第一和第二道工序分別由兩臺不同的CNC 依次加工完成.在情況1 的基礎上，RGV 增加2 種不同的狀態，即是否載有第一道工序加工完成的物料.由于物料調度復雜提高，建立優化的RGV 動態調度算法，在該算法中，主要通過優化RGV、CNC 的狀態.

表6 不同情況的RGV 狀態對比

首先，我們要確認安裝兩種不同刀具的CNC 數量分配比例，根據CNC 加工完成一個兩道工序的物料過程中第一和第二道工序所需的時間，進行對比.對比效率＝1/CNC加工時間，得到表7 的分配比例.

表7 每組數據的刀具分配比例

由表7 可得，我們發現每個配比均為非整數的，由整數規劃中的分支定界法可得，每個比例可能的整數解有兩種.我們先假設其比例效果與CNC 的位置分布無關，僅與CNC 刀具配比數量有關.但經驗證，發現預測是有偏差的，若忽略CNC 位置分布進行調度，那么加工完成的物料數將會減少.

設RGV 狀態為二進制變量，當RGV 狀態為0 時，表示沒有載有第一道工序加工完成的物料，此時應調度到裝有TP1的CNC 處；當RGV 狀態為1 時，表示載有第一道工序加工完成的物料，此時應調度到裝有TP2的CNC 處；基于CNC 僅加工一道工序的模型，我們將針對每一種刀具的分配比例TP1：TP2進行迭代計算，得到結果如表8所示.

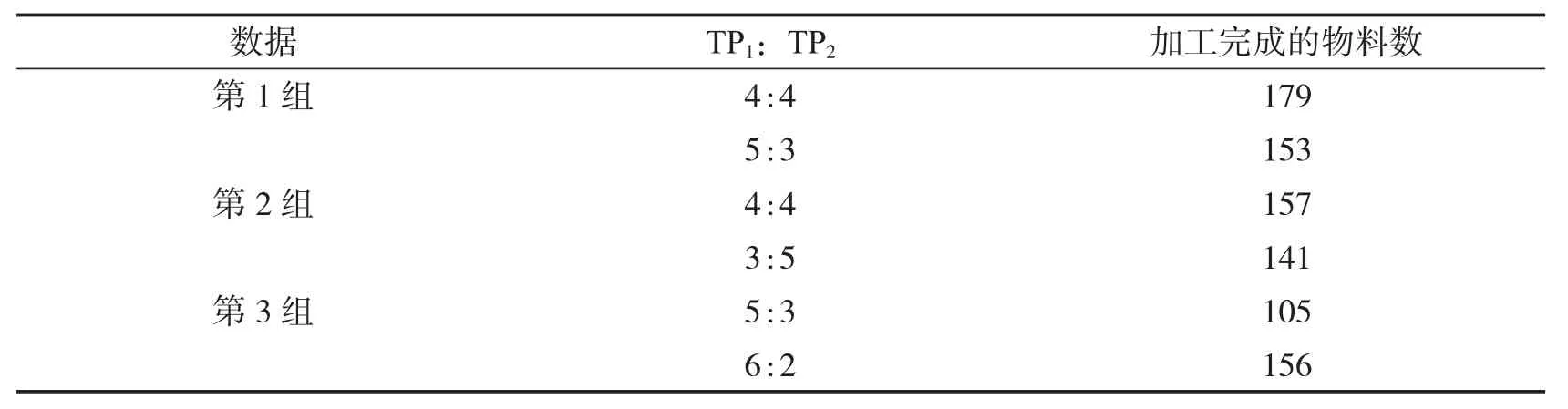
表8 CNC 僅加工兩道工序的刀具配比及加工完成的物料數

2.5.3 基于空閑時間插入法的故障擾動模型的結果

經過MATLAB 求解，得到調度策略和8 h 內的系統作業效率，其結果部分如表9、10 所示.

表9 第1 組數據：一道工序有故障

表10 第1 組數據：兩道工序有故障

3 任務二：仿真檢驗

3.1 任務2的分析

任務2 要求用表1 的三組數據檢驗任務1 中模型的實用性以及算法的有效性.為了達到此目標，我們可以構建可視化仿真模型.我們通過Tecnomatix Plant Simulation 生產加工仿真軟件構建了智能RGV 動態調度可視化仿真驗證模型.該軟件具有豐富且實用的處理功能，可以方便的選擇系統零件、設置參數以及搭建路徑.我們可以將仿真得到的結果與建立動態路徑調度模型的結果進行比較，以檢驗模型的實用性和算法的有效性.基于仿真結果和模型結果，給出調度策略和系統的作業效率.最后把模型驗證的具體結果分別填入EXCEL 表中.

3.2 TPS可視化仿真

為了驗證模型的實用性和算法的有效性，根據文獻[4]的仿真方法，我們用Tecnomatix Plant Simulation 仿真軟件（以下簡稱“TPS”）輸入的三組數據進行模擬仿真，導出相關數據，與算法計算結果比較，從而達到驗證的目的，如圖4（a）所示.

選擇TPS 作為模型驗證的仿真軟件主要的原因是：TPS 具有模型所需要的所有對應實物的對象，比如有模擬RGV 的“小車”，“裝配”模擬CNC 加工臺等，這樣就不需要自己創建對象，使得模擬出來的數據更加符合實際.并且TPS 生產加工仿真系統中自帶可設置CNC 故障率，這給我們的仿真驗證模型帶來了極大的便利，設置CNC 故障率為1%，即仿真模型中CNC 組件可用性為99%，如圖4（b）所示.

在原始智能加工系統的TPS 模擬仿真模型基礎上，設物料輸入服從均勻分布.并且對任務1 中的每種情況進行設置.經過比對，仿真模型結果與我們算法得到的結果相同.這說明我們建立的模型具有實用性，我們建立的算法也是有效的.因此，我們可以根據所建立的模型作為實際調度策略的應用，系統的工作效率由成料產出除以每班次的時間得出.

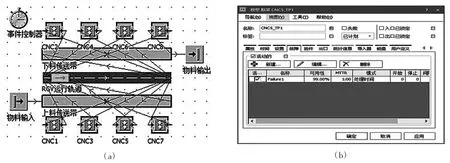
圖4

4 總結

本文通過建立了不同情況下的動態調度模型，完整解決了任務1 和任務2.我們利用圖論和規劃論的內容，將復雜的實際問題轉化為數學模型，并利用仿真算法精準地模擬了RGV 的決策過程、旅行過程和作業過程.在模型逐漸復雜化的情況下，對原有模型添加約束條件，使得其能更好地模擬實際問題.通過增加狀態變量，縮小RGV 決策集等方法優化了算法.基于得到的算法，可以編寫對應的程序，從而得到RGV 的調度策略和系統的作業效率.最終的模型和算法實用性較強，可以應用于實際的動態調度中.