小樣本條件下基于Bayes方法的裝備狀態評估

谷廣宇 劉建敏 喬新勇

摘要：??針對小樣本條件下單純采用使用期無法準確衡量裝甲裝備技術狀況的問題，本文以裝甲車輛發動機狀態評估為例，分析了小樣本條件下，裝備各技術狀況等級特征參數分布及其有效性和適用性。同時，采用Bayes決策法，從裝備屬于各技術狀況等級的概率和錯判風險兩方面出發，對裝備狀態進行評估。評估結果表明，利用兩種Bayes方法均能準確評估發動機技術狀況，評估準確率達90%以上，并且基于最小風險的Bayes評估方法具有更好評估效果，評估準確率較高，符合裝甲車輛技術狀況隨使用時間增加而逐漸變差的一般規律。該方法在裝備狀態評估中具有實用性及可行性。

關鍵詞：??狀態評估;?小樣本;?Bayes決策法;?發動機

中圖分類號：?TK428;?E923.1?文獻標識碼：?A

收稿日期：?2019-03-25;?修回日期：?2019-06-27

基金項目：??國家自然科學基金資助項目（U1836101）

作者簡介：??谷廣宇（1989-），男，漢族，博士研究生，主要研究方向為發動機狀態評估與預測。

裝甲裝備在使用過程中，其技術狀況將隨著使用時間的增長發生變化，且呈現劣化趨勢。雖然其技術狀況在一定程度上可以采用運行時間來衡量[1]，但由于使用環境、使用強度及工作地點等因素不盡相同，該方法有時不能完全真實地反映裝備的實際技術狀況。因此，需要運用科學的方法對裝甲裝備進行技術狀況評估[2]。通常情況下，在裝備的狀態檢測評估過程中，首先要采集裝備狀態信息，并對數據樣本進行統計分析，才能得到相關結論。目前，基于數據驅動的評估方法主要有模糊聚類[3]、支持向量機[4]、神經網絡[5]、Bayes決策法[6]等。這些方法就統計分析而言，均需要盡可能大的樣本量，然而在實際評估過程中，受試驗成本、試驗周期等條件影響，無法進行大量試驗來獲取大樣本。在此情況下，仍采用傳統大樣本條件下的統計方法，難以保證其最終得到評估結果的可靠性。因此，研究在小樣本條件下的狀態檢測評估方法具有實際意義[7]。另外由于在狀態信息采集測量過程中，用以描述各個技術狀況的特征參數都是隨機變量，同一技術狀況下所有采集測量的樣本只可能是相似的，不可能完全一樣，而且某一特征值可能不只出現在某一特定狀況下，在其他狀況中也可能出現。鑒于Bayes決策理論既能參考各類狀態的分類錯誤率，又能考慮分類錯誤的風險程度，具有較強的分類決策能力。因此，本文采用Bayes決策法對裝備技術狀況進行評估，并利用小樣本統計方法構造各技術狀況下特征參數的分布，以獲取Bayes決策中的類條件概率密度。該研究可以對即將變“差”的車輛提前進行預防性維修，降低故障風險。

1?小樣本統計原理與方法

為提高統計分析精度，在小樣本條件下，最有效的解決方法是設法增加信息量。在此類方法中，以美國斯坦福大學B.Efron教授提出的Bootstrap法[8]及B.R.Donald提出的Bayes?Bootstrap法[9]最為簡單有效，而且在工程應用中取得了豐碩成果[10-13]。其基本思路都是依據現有小樣本模仿未知分布，進而獲取再生樣本，將小樣本問題轉化成大樣本。因此，該方法適用于本文對不同技術狀況下小樣本狀態信息的統計分析。

1.1?Bootstrap方法

Bootstrap方法又稱自助估計法，其原理主要根據觀測到來自于未知總體分布F的隨機子樣X=（X1，…，Xn），估計總體分布F的某一分布特征R（X，F），如均值、方差等，從而推測總體分布F。具體方法如下：

設總體分布F的某個分布特征θ=θ（F）（如均值，方差等），由觀測子樣X=（X1，…，Xn）構造經驗分布Fn，則有對θ的估計=（Fn），估計誤差為

Tn=（Fn）-（F）（1）

根據經驗分布Fn，重新抽取再生子樣X（1）=（X（1）1，…，X（1）n），進而構造經驗分布函數F（1）n。于是由X（1）又可得到θ的估計（F（1）n）。此時，可得到估計誤差Tn的Bootstrap統計量R（1）n，即

R（1）n=（F（1）n）-（Fn）（2）

重復抽取多組再生子樣X（i），i=1，2，…，m，可計算相應R（i）n，i=1，2，…，m，并利用R（i）n的分布去逼近Tn的分布，并根據式（1）得到θ（F）的樣本，即

θ（i）（F）=（Fn）-Tn≌（Fn）-R（i）n（3）

該方法與傳統統計方法相比，在小樣本估計中具有較高精度。

1.2?Bayes?Bootstrap方法

Bayes?Bootstrap方法，即隨機加權自助法，也是將子樣信息“提攜”的方法，是對Bootstrap方法的改進。其原理主要利用Dirichilet隨機向量對子樣X=（X1，…，Xn）進行加權，從而計算隨機加權統計量Dn，進而利用Dn模仿估計誤差Tn的分布。具體方法如下：

設子樣X=（X1，…，Xn）來自于未知總體分布F，μ和σ2為F的未知期望和方差，和S2為X的統計期望和方差，則估計誤差為

T1=-μ（4）

T2=nn-1S2-σ2（5）

式中，T1和T2為期望的估計誤差和方差的估計誤差。生成N個參數為（1，…，1）的Dirichilet隨機向量Vi=（vi1，vi2，…，vin），i=1，2，…，N，可獲取隨機加權統計量為

Di1=∑nk=1vikxk-（6）

Di2=nn-1∑nk=1vik（xk-）2-nn-1S2（7）

利用Di1和Di2模仿估計誤差T1和T2的分布，根據式（4）和式（5），可得

μ=-T1≈-1（8）

S2=nn-1S2-T1≈nn-1S2-2（9）

已有成果的實際應用及仿真計算表明，該方法分析精度較高于Bootstrap方法[14]。

2?Bayes決策理論

Bayes決策理論是模式識別問題中經典的分類決策理論，其基本思想是通過各狀態下的先驗概率分布推定后驗概率[15]。根據決策規則，Bayes決策又分為基于最小錯誤率[16]和基于最小風險的Bayes決策[17]。

2.1?基于最小錯誤率的貝葉斯決策

假設共有m個決策狀態總體W=（w1，w2，…，wm），已知其先驗概率P（wi），i=1，2，…，m，依據前文小樣本統計理論可推定各狀態下特征參數x的分布模型，并獲得其類條件概率密度P（x|wi）。則根據Bayes公式，可得各狀態后驗概率為

P（wi|x）=P（x|wi）P（wi）∑mi=1P（x|wi）P（wi）（10）

并有決策規則：若P（wi|x）=max＼[P（wi|x）＼]，則x∈wi。此類決策規則稱為基于最小錯誤率的貝葉斯決策。

2.2?基于最小風險的貝葉斯決策

實際決策過程中除了錯誤率外，有時也需要考慮決策錯誤所帶來的風險，在這種情況下，通常可以選擇基于最小風險的貝葉斯決策方法[18]。

基于最小風險的貝葉斯方法在基于最小錯誤方法上引入了“損失”的概念，即把屬于wi的狀態錯判為aj狀態的損失，可記為cji，一般決策損失表如表1所示。

根據表1及前文所得后驗概率，可計算決策為wi的狀態條件風險為

R（wi|x）=E＼[c（i|j）＼]=∑mj=1c（j|i）P（wj|x）（11）

并有決策規則：若R（wi|x）=min＼[R（wi|x）＼]，則x∈wi。

3?應用實例

基于貝葉斯方法的裝備狀態評估，實質上就是將裝備的技術狀況劃分為從優到劣幾個等級的問題，本文以裝甲車輛發動機狀態評估為例，并依據摩托小時（使用時間）將其技術狀況分為“優”、“良”、“一般”、“較差”、“差”這5個等級，分別以“0～200”，“200～300”，“300～400”，“400～500”，“500～600”這5個階段統計特征表示，即有W=（w1，w2，w3，w4，w5）={“優”，“良”，“一般”，“較差”，“差”}。

3.1?特征提取

評估發動機技術狀況的參數很多，但實踐證明，通過減速時間評估技術狀況是一種簡單有效的辦法[19]，因此本文選取柴油機減速時間作為技術狀況評估的特征參數。減速時間是指發動機在最高空轉轉速下運轉時迅速停止供油，使其自行減速，計算從最高空轉轉速減到轉速為0的時間。隨著使用時間增長，發動機活塞缸套磨損增加，阻力減小，減速時間將變長[20]。

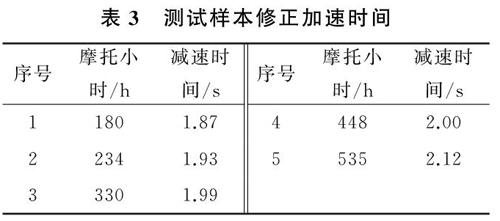
發動機瞬時轉速如圖1所示，將實際計算瞬時轉速從n3減速到n4的時間作為發動機減速時間，此時取n3=2?200?r/min，n4=800?r/min。

依此方法在5種技術狀況等級下，分別對同一型號6輛不同摩托小時的裝甲車輛進行測試，提取減速時間，并作為統計樣本，用以計算該等級下分布特征，以檢驗本文評估方法的準確性。另外，隨機抽取5輛未知狀況的裝甲車，提取修正減速時間作為測試樣本，利用本文方法對其進行評估。統計樣本減速時間如表2所示，測試樣本減速時間如表3所示。

3.2?小樣本統計

假設發動機減速時間在各個使用階段均服從正態分布，利用Bayes?Bootstrap小樣本統計方法，對各個階段減速時間進行統計，根據式（4）～式（9），得各階段分布的均值和標準差，Bayes?Bootstrap法下各技術狀況分布特征如表4所示，各技術狀況等級分布特征如圖2所示。由表4和圖2可以看出，減速時間隨技術狀況等級變化較為明顯，因此能夠較好地反映發動機技術狀況的變化。

3.3?基于Bayes決策的狀態評估

由于測試車輛摩托小時在0～600?h內呈均勻分布，因此各狀態的先驗概率為

P（W）=＼[1/3，1/6，1/6，1/6，1/6＼]

考慮評估過程中錯誤率的存在，根據經驗，引入發動機狀態評估決策損失C，發動機狀態評估決策損失如表5所示。

3.4?評估準確性對比

根據表4及式（10）和式（11），分別利用兩種Bayes方法對統計樣本進行評估，統計樣本評估結果如表6所示。

由表6可以看出，利用兩種Bayes方法均能夠準確評估發動機技術狀況，評估準確率達90%以上，并且基于最小風險的Bayes評估方法具有更好評估效果。

3.5?測試樣本狀態評估

采用基于最小風險的Bayes評估方法，對表3測試樣本進行評估，在5種狀態下，各測試樣本的條件風險及評估結果如表7所示。

由表7可以看出，評估結果符合裝甲車輛技術狀況隨使用時間增加而逐漸變差的一般規律，證明該方法在裝備狀態評估中的實用性及可行性。

該方法還能判斷測試樣本的變化趨勢，例如測試樣本1根據表7被評估為“優”狀態，但其“良”狀態的風險與“優”狀態只有很小差別。因此，可判斷該樣本接近“優”狀態與“良”狀態的邊緣，即將退化為“良”狀態。依據該方法可以對即將變“差”的車輛提前進行預防性維修，以降低故障風險。

4?結束語

本文通過結合Bootstrap小子樣統計方法及Bayes決策法，有效地解決了小樣本條件下的裝甲裝備狀態評估的問題，并以裝甲車輛發動機為例，驗證了該方法的有效性。采用Bootstrap小子樣統計方法，能夠有效擴充發動機狀態參數樣本，實現小樣本條件下的裝備狀態評估的先驗統計;Bayes決策法在裝備狀態評估過程中，不但考慮了各技術狀況出現的概率，還考慮了錯誤評估的風險，比其他技術狀況評估方法更具合理性;采用本文方法進行裝甲車輛發動機的技術狀況等級評估，評估結果較符合實際規律，正確率可達90%以上。該研究具有一定工程實用性及可行性。

參考文獻：

[1]?李國錦.?基于層次分析及模糊綜合評判的裝甲車輛發動機狀態評估[J].?車輛與動力技術，?2017（4）：?40-44.

[2]?張會奇，?陳春良，?劉峻巖，?等.?基于BP神經網絡的裝甲車輛發動機使用狀態評價[J].?兵工自動化，?2014，?33（1）：?32-34.

[3]?辛江慧，?鄒政耀，?任成龍.??基于灰色定權聚類的混合動力汽車發動機運行狀態評估[J].??重慶理工大學學報：自然科學，?2014，?28（7）：?26-29.

[4]?汪瑾，?陳果，?王洪偉，?等.??基于后驗概率SVM的航空發動機滾動軸承狀態評估[J].??軸承，?2015（5）：?55-59.

[5]?劉伯運，?歐陽光耀，?常漢寶.??基于神經網絡和DS證據理論的柴油機狀態評估[J].??車用發動機，?2005（5）：?14-17.

[6]?朱偉明.??基于貝葉斯融合的柴油機性能狀態評估方法研究[J].??內燃機，?2010（2）：?18-19，?36.

[7]?高攀東，?陳曉陽，?沈雪瑾，?等.??小樣本下軸承可靠性評估方法對比分析[J].??軸承，?2014（12）：??44-48.

[8]?Efron?B，?Tibshirani?R?J.??An?introduction?to?the?bootstrap[M].??London：?Chapman?and?Hall，?1993.

[9]?Donald?B?R.??The?bayesian?bootstrap[J].??The?Annals?of?Statistics，?1981，?9（1）：?130-134.

[10]?李會鵬，?明廷鋒，?賀國.??小樣本條件下一種旋轉機械振動狀態閾值的確定方法及應用[J].??武漢理工大學學報：?交通科學與工程版，?2012，?36（5）：?1059-1063.

[11]?喬新勇，?劉建敏，?張小明.??小子樣統計理論在裝備狀態檢測中的應用[J].??裝甲兵工程學院學報，?2009，?23（2）：?41-43，?87.

[12]?唐雪梅，?周伯昭，?李榮.??武器裝備小子樣綜合試驗設計與鑒定技術[J].??戰術導彈技術，?2007（2）：?51-56，?79.

[13]?袁?鵬，?張衛兵，?韓自剛.?銀川地區建筑地基沉降計算驗系數取值[J].?科學技術與工程，?2017，?17（20）：??236-240.

[14]?樊鶴紅，?劉盼，?趙興群，?等.??小樣本條件下行波管可靠性評估方法的研究[J].??電子學報，?2010，?38（6）：?1394-1398.

[15]?張湘平，?張金槐，?謝紅衛，?等.??基于隨機加權法的BAYES精度評定[J].??國防科技大學學報，?2001，?23（3）：?98-102.

[16]?全星慧，?牟海維，?呂秀麗，?等.??基于PCA與貝葉斯決策的人臉識別算法[J].?光學儀器，?2014，?36（2）：?122-125.

[17]?徐智康，?李旸，?李德玉.?基于可變最小貝葉斯風險的層次多標簽分類方法[J].?南京大學學報：?自然科學版，?2017，?53（6）：?1023-1032.

[18]?毛思敏.??基于最小風險貝葉斯準則的工業過程故障診斷[D].?武漢：華中科技大學，?2016.

[19]?張更云，?何來龍.??一種評價發動機實際技術狀況的方法[J].??裝甲兵工程學院學報，?2005，?19（4）：?67-70.

[20]?張小明，?劉建敏，?喬新勇，?等.?柴油機健康狀況評估及其方法[J].?裝甲兵工程學院學報，?2008，?22（2）：?30-34.

Equipment?States?Evaluation?Based?on?Bayes?Method?with?Small?Sample

GU?Guangyu，?LIU?Jianmin，?QIAO?Xinyong

（Vehicle?Engineering?Department，?Army?Academy?of?Armored?Forces，?Beijing?100072，?China）

Abstract：??In?order?to?solve?the?problem?that?the?technical?condition?of?armored?equipment?can?not?be?accurately?measured?by?using?the?service?life?alone?under?the?condition?of?small?sample，?this?paper?takes?the?engine?state?evaluation?of?armored?vehicle?as?an?example，?and?analyzes?the?effectiveness?and?applicability?of?the?characteristic?parameters?distribution?in?each?technical?condition?of?the?equipment?under?the?condition?of?small?sample.??At?the?same?time，?the?Bayes?decision?method?is?used?to?evaluate?the?equipment?status?from?two?aspects：??the?probability?of?the?equipment?belonging?to?each?technical?condition?grade?and?the?misjudgment?risk.??The?evaluation?results?show?that?both?Bayes?methods?can?accurately?evaluate?the?engine?technical?status，?and?the?evaluation?accuracy?is?larger?than?90%.??The?Bayes?evaluation?method?based?on?minimum?risk?has?better?evaluation?effect?and?higher?evaluation?accuracy，?which?accords?with?the?general?law?that?the?technical?condition?of?armored?vehicles?becomes?worse?with?the?increase?of?service?time.??This?method?is?practical?and?feasible?in?equipment?condition?evaluation.

Key?words：??states?evaluation;?small?sample;?Bayes?decision;?engine