基于有限質點法的含間隙鉸平面機構動力分析

鄭延豐，楊 超，劉 磊，羅堯治

(1.浙江大學空間結構研究中心，浙江，杭州 310058；2.浙江省空間結構重點實驗室，浙江，杭州 310058；3.浙江綠城元和房地產開發有限公司，浙江，杭州 310058)

在常規的平面機構動力分析中，一般認為平面鉸節點處于沒有間隙的理想狀態。但由于制造和安裝誤差，鉸節點中不可避免地存在間隙。間隙的存在使得鉸節點的軸承和軸頸易發生碰撞，從而使帶間隙機構的動力響應與理想機構不同。近年來，學者們對間隙的力學模型和含間隙鉸平面機構的動力行為開展了研究。彈簧-阻尼模型是經典的線性間隙接觸力模型，但在接觸瞬間和分離瞬間的接觸力是不連續的[1]。Hertz[2]基于純彈性理論提出了非線性的接觸力模型，但沒有考慮接觸碰撞過程中的能量損失。Lankarani和 Nikravesh[3]提出了考慮彈性剛度項和阻尼項的接觸法向力模型，可以考慮接觸過程中的能量損失。Bai和Zhao[4]基于已有的間隙接觸力模型提出了一種用于平面帶間隙機構的混合接觸力模型。Zhang等[5]研究了間隙鉸節點對平面3-RRR機構動力行為的影響。在含間隙機構的動力問題中，若機構中含有多個間隙鉸，則不同間隙鉸之間的相互作用將使動力響應變得復雜[6]。若機構構件是柔性的，則在驅動力作用下構件將發生彎曲變形，從而改變間隙鉸的動力行為[7]。

機構屬于可變結構體系，其運動過程的模擬與常規結構存在較大差異。采用隱式求解的線性有限元方法在處理可變體系上存在困難，因為其集成的整體剛度矩陣是奇異的。非線性有限元法可用于機構問題求解，其中，幾何精確方法(geometrically exact beam theory)[8]以轉動參數為廣義坐標，通過精確的幾何非線性關系描述機構的變形，計算效率和計算精度高，但轉動參數的更新和奇異性是該方法的難題。絕對節點坐標法(absolute nodal coordinate formulation, ANCF)[9]采用位移場的斜率矢量避免復雜的轉角問題，建模直觀，但自由度多，計算效率低下，同時收斂性也存在問題。多體系統動力學可用于模擬帶間隙機構的動力響應[10－12]，但隨著間隙節點數量的增加，約束多體系統逐漸變為無約束或節點-力系統[13]；并且由于間隙節點之間的相互作用，其動力行為變得更加復雜。

有限質點法(finite particle method, FPM)是基于向量式有限元發展的、面向結構行為的分析方法，已應用于動力、幾何非線性、材料非線性、屈曲/褶皺失效、機構運動、接觸碰撞、斷裂等結構復雜行為分析[14]。在有限質點法中，采用顯式求解方案，不需集成整體剛度矩陣，因此可避免剛度矩陣奇異，用于機構運動分析時不會存在困難[15]。有限質點法將結構離散為質點，以質點代表結構的運動，間隙碰撞產生的接觸力可直接作用于質點，不需要對剛度矩陣進行修正。因此基于有限質點法引入含間隙鉸的分析方法在原理上是可行的，在處理上也十分方便，可為更精細的機構運動模擬提供手段。

本文基于有限質點法，對含間隙鉸的平面機構開展動力分析。首先給出有限質點法平面機構分析的原理，包括質點運動控制方程和平面梁單元的內力計算公式。然后引入Lankarani-Nikravesh模型和修正庫侖摩擦模型，來計算間隙鉸中軸承和軸頸碰撞過程中的接觸力和摩擦力。最后以幾個典型的平面機構為例開展動力分析，研究間隙鉸對機構動力響應的影響。本文的創新點包括以下兩個方面：1)將有限質點法用于求解含間隙機構動力問題，拓展了有限質點法的應用領域，也為這類問題的求解提供一種有效手段；2) 該方法建模直觀，編程簡單方便，不僅可求解單間隙鉸、剛性機構的動力問題，還可用于多間隙鉸、柔性機構問題的動力分析。

1 有限質點法平面機構分析原理

在有限質點法中，平面機構被離散成質點，代表機構的位置、質量、受力、變形和邊界條件，即點值描述。機構桿件被離散為平面梁單元，但單元的概念和作用被弱化，僅用于表示質點之間的相互作用關系。在時間域上，質點受力后的運動軌跡被劃分成許多離散的微段，并通過一組時間點上的值來描述各個質點的位移，即途徑單元描述。

1.1 質點運動控制方程

離散模型中所有質點的運動都遵循牛頓第二定律。對于平面梁單元連接的質點，其運動變量可分解為沿平面坐標軸方向的2個線位移和1個角位移，分別對應坐標軸方向的2個力和1個彎矩，如圖1所示。

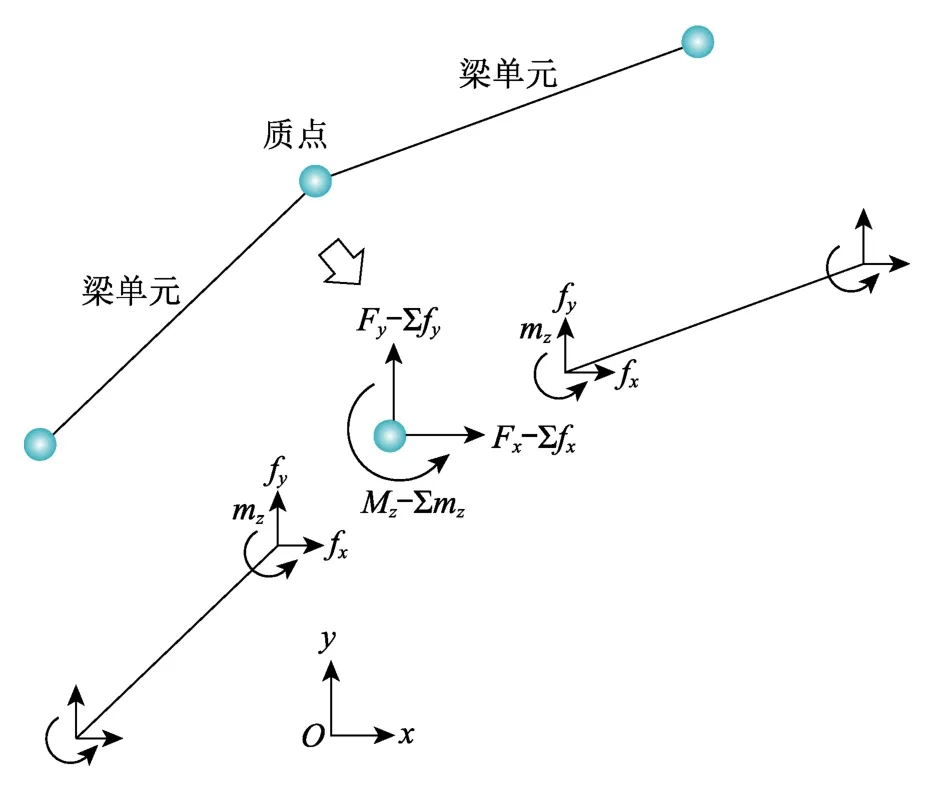
圖1 平面機構的質點受力Fig.1 Particle force of planar mechanisms

平面機構的質點運動方程可具體表達為：

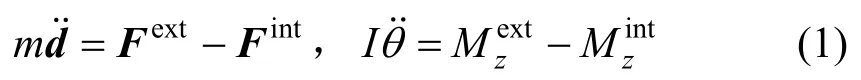
式中：m為質點的質量；d=[dx,dy]T為質點線位移向量；Fext=[Fx,Fy]T為質點外力向量；Fint=為梁單元傳遞至質點的內力向量；I為質點的質量慣性矩；θ為質點角位移；為質點外力矩；為各個梁單元傳遞至質點的內力矩。質點的質量m和質量慣性矩I可通過下式集成：

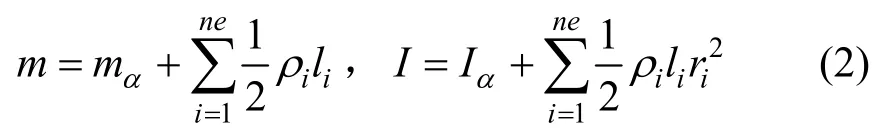
式中：mα和Iα分別為質點α的集中質量和集中質量慣性矩；ne為與質點相連的梁單元數量，對第i個梁單元；iρ為其線密度；li為長度；ri為截面回轉半徑。

有限質點法采用顯式積分方案，可由中心差分法估算質點的加速度和角加速度：

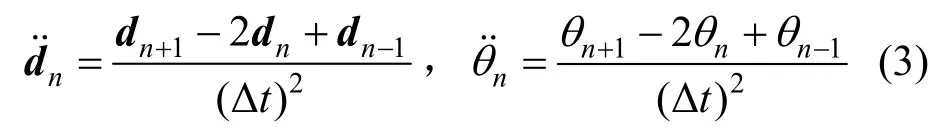
式中，Δt為時間積分步長。將式(3)代入式(1)，可由n-1和n時刻位移得到n+1時刻位移，同理可得n+1時刻角位移，如式(4)所示。迭代求解，可得結構在外荷載下的位移反應。

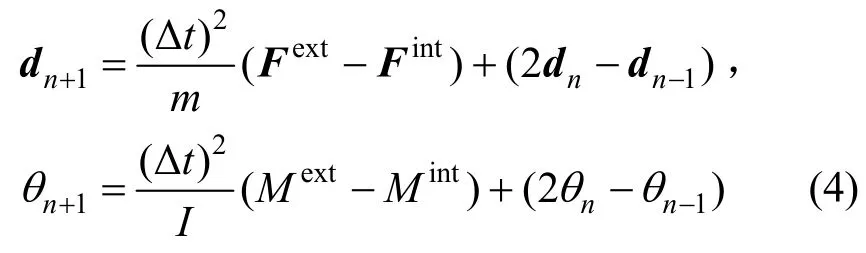
為使計算收斂，計算步長需要小于臨界時間步長。本文采用的平面梁單元臨界時間步長Δtmin可按下式估算[16]：

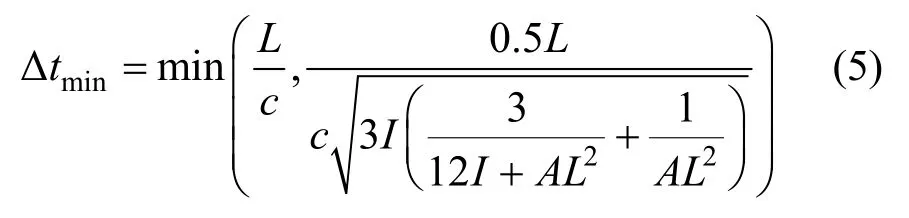
式中：L為梁單元長度；為波速；E為彈性模量；L、A和I分別為梁單元的長度、截面積和截面慣性矩。由于間隙處存在接觸非線性行為，因此本文建議將Δtmin乘以小于1的系數tα(建議取0.5左右)，以保證計算收斂。

1.2 平面梁單元內力

喻瑩[17]推導了有限質點法三維梁單元的內力計算公式。退化到二維，可得到平面梁單元的內力計算公式[15]。設梁單元AB在ta和tb( =ta+ Δt)時刻的平面位置分別為節點轉角分別為則單元從ta到tb時刻的位移和轉角分別為：

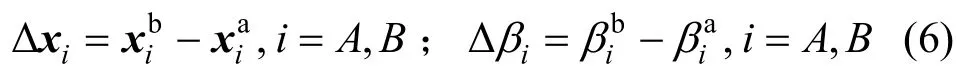
ta和tb時刻單元主軸方向向量分別為：

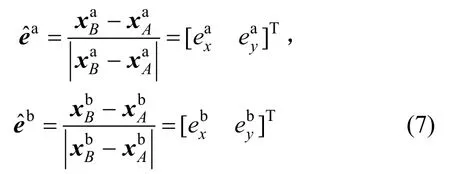
則兩軸之間的轉動角度為：

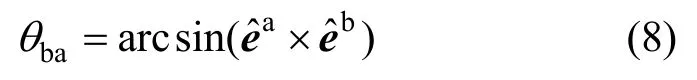
單元位置從ta時刻的AB運動到tb時刻的A′′B′。為計算單元純變形，將單元進行逆向運動，如圖 2所示。逆向平移量為-ΔxA，逆向轉動角度為-θba。由于單元變形后仍為直線，虛擬位置A′′B′′與AB共線。在單元的虛擬位置，得到單元的純變形為：

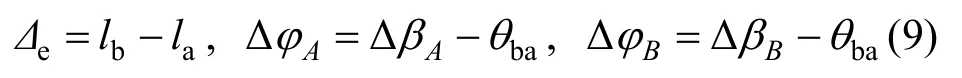
式中，l為梁單元的長度。

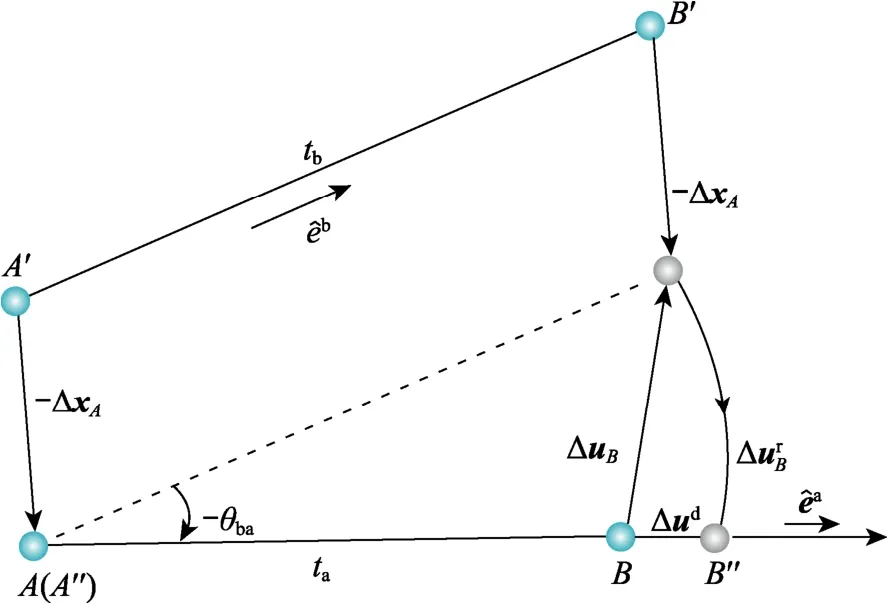
圖2 平面梁單元的虛擬逆向運動Fig.2 Fictitious reversed rigid-body motion of planar beam element

局部坐標系下，單元在途徑單元的內力增量為：

式中，Iz為截面轉動模量。將單元內力增量疊加到ta時刻參考構型的內力全量上，轉換至整體坐標系，再將單元經過正向平移ΔxA和正向轉動θba，可得到平面梁單元tb時刻的單元內力。平面內的平移和轉動對單元彎矩的方向和大小沒有影響，因此不需對單元彎矩進行處理。單元內力tb時刻的內力為：

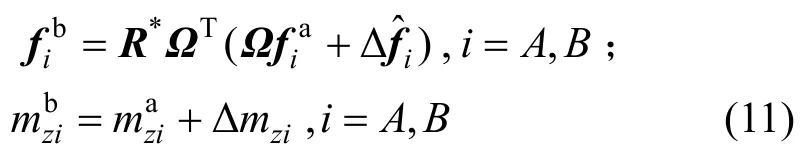
式中：?為單元局部坐標系和整體坐標系的轉換矩陣；R*為旋轉矩陣，如下式所示：

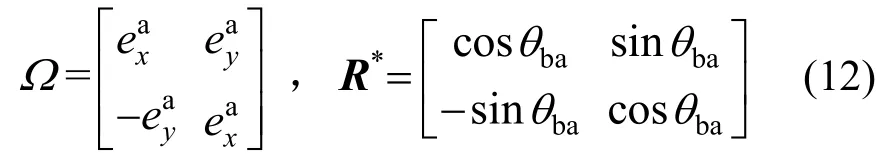
2 平面轉動鉸模型

2.1 理想轉動鉸模型

在平面機構中，轉動鉸是由軸承和軸頸構成的。理想轉動鉸中軸承和軸頸的相互作用力可通過運動約束條件推導得到，如圖3(a)所示。設軸承和軸頸的中心點分別為B和J，其運動控制方程為：

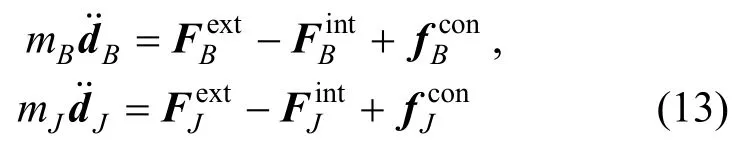
將式(14)代入式(13)得：

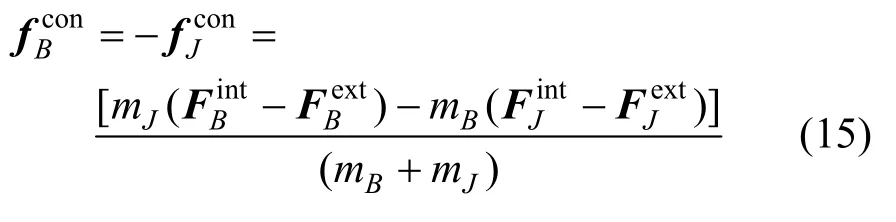
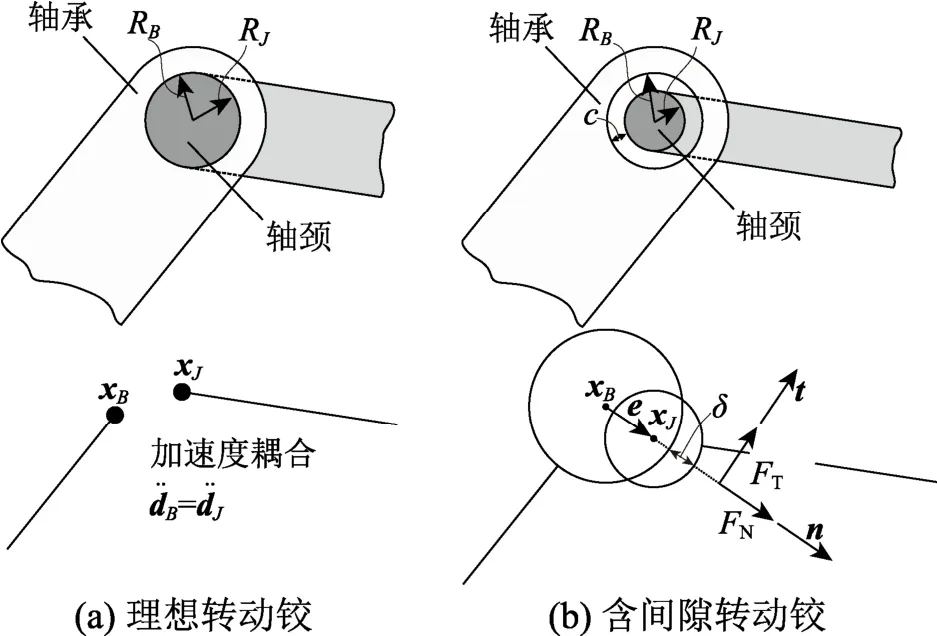
圖3 理想轉動鉸和含間隙轉動鉸的力學模型Fig.3 Mechanical model of ideal revolute joint and revolute joint with clearance

2.2 含間隙轉動鉸模型

含間隙的轉動鉸中軸承與軸頸的相互作用力可根據軸承和軸頸的接觸情況推導得到。

2.2.1 接觸偵測

對含間隙的轉動鉸(圖3(b))，雖然軸頸的運動受到軸承的約束，但有一定的自由運動空間。軸頸在軸承中有自由運動、碰撞、接觸三種不同的運動狀態。在自由運動狀態中，軸頸在軸承的內圈邊界內自由運動，軸頸與軸承間無接觸和相互作用力。碰撞狀態是一個臨界狀態，出現時間極短，發生在自由運動結束時，碰撞力作用在轉動鉸中且很快消失，該狀態的運動和動力特性是離散的，兩個碰撞體之間發生有效的動量轉化。碰撞結束后，軸頸可能進入接觸或者自由運動狀態。在接觸狀態，軸頸與軸承始終保持接觸且相互之間做滑行運動，侵入深度隨軸頸運動而不斷變化；這種狀態隨著軸頸與軸承的分離而終止，后續軸頸進入自由運動狀態。

接觸狀態可通過間隙大小及軸承、軸頸的相對位置判斷。如圖3(b)所示，轉動鉸的間隙大小為：

式中：RB和RJ分別為軸承的內半徑和軸頸的外半徑；OB和OJ分別為軸承和軸頸的中心，坐標分別為xB和xJ。則連接軸承和軸頸中心的偏心向量e可以表示為：

軸頸與軸承相互碰撞導致的侵入深度δ可表示為：

軸頸與軸承碰撞平面的法向單位向量n和偏心距向量在同一條直線上。為計算接觸力和摩擦力，在接觸點處建立局部坐標系(n,t)：

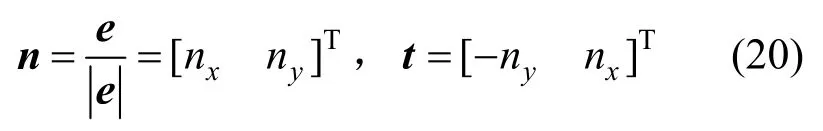
2.2.2 法向接觸力

本文采用Lankarani-Nikravesh模型[3]計算間隙產生的法向接觸力。Lankarani和Nikravesh[3]基于Hertz接觸理論，提出了非線性的彈簧阻尼模型。該模型將法向接觸力表示為侵入深度的函數，并考慮了接觸點的局部變形及接觸過程的持續時間；同時引入與回彈系數、侵入速度相關的粘滯阻尼項來反映材料阻尼導致的能量損失，可考慮碰撞體材料的屬性、局部變形、碰撞速度等因素的影響。因此國內外的學者廣泛地應用該模型對含間隙機構動力學進行分析研究。

Lankarani-Nikravesh模型的接觸力公式為：

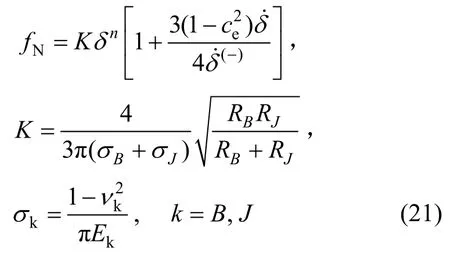
式中：ce為恢復系數；νk為泊松比；Ek為彈性模量；為初始碰撞時刻碰撞點的相對運動速度；為接觸過程中的瞬時侵入速度；n為非線性系數，一般可取1.5。

2.2.3 切向摩擦力

本文采用修正庫侖摩擦模型[18]來計算切向摩擦力。為簡便起見，假設軸承和軸頸間的摩擦為滑動摩擦。滑動摩擦力大小可由下式計算：

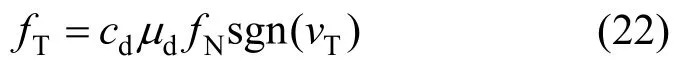
式中：μd為動摩擦系數；sgn(?)為符號函數；cd為修正系數：

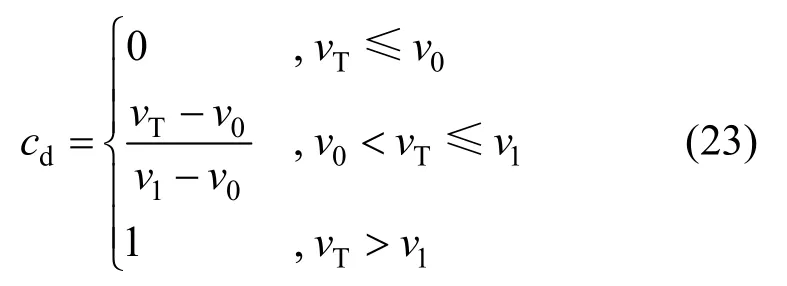
式中：v0和v1為臨界系數，可按經驗取值；vT為軸頸和軸承在接觸點的相對切向速度。修正系數cd可避免當vT接近零值時摩擦力的突然變向。

vT可按以下方法計算：軸承和軸頸在接觸點Q處的坐標可表示為：

將其對時間求導，可得對應的速度：

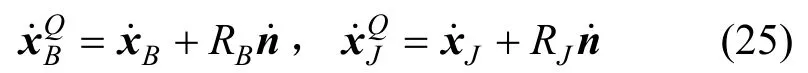
則相對切向速度vT和法向速度vN可以通過投影得到：

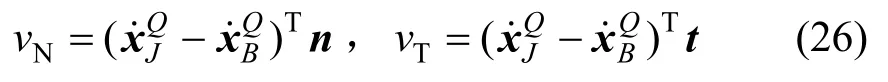
2.2.4 接觸力集成

計算出軸頸和軸承之間的法向接觸力和切向摩擦力后，軸頸和軸承對應質點所受總的接觸力可表示為：

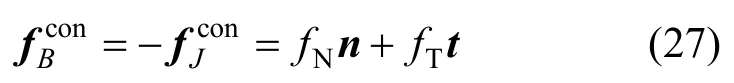
式中，fN和fT分別為法向接觸力和切向摩擦力。法向接觸力通過軸承和軸頸的中心，不會產生附加力矩。但摩擦力是沿接觸點切向的，會對軸頸或軸承中心產生附加力矩。附加力矩大小為：

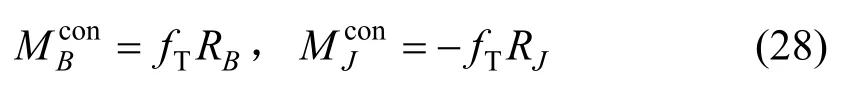
軸頸和軸承對應質點的運動控制方程可寫為：

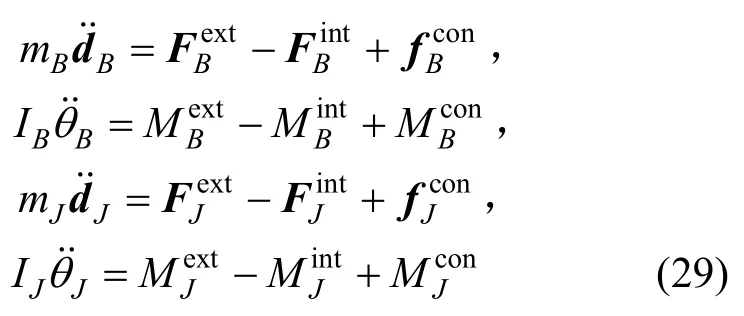
以上運動控制方程的求解與一般質點類似。

2.3 計算流程

通過對軸頸和軸承的接觸偵測、接觸力和摩擦力計算、接觸力集成，即可求解各質點位移，進入下一時刻，更新平面梁單元內力，計算質點合力，從而迭代求解出結構運動過程中各時刻的位移。完整的計算流程如圖4所示，其中的突出標識為在原算法基礎上增加的考慮間隙接觸的計算步驟。

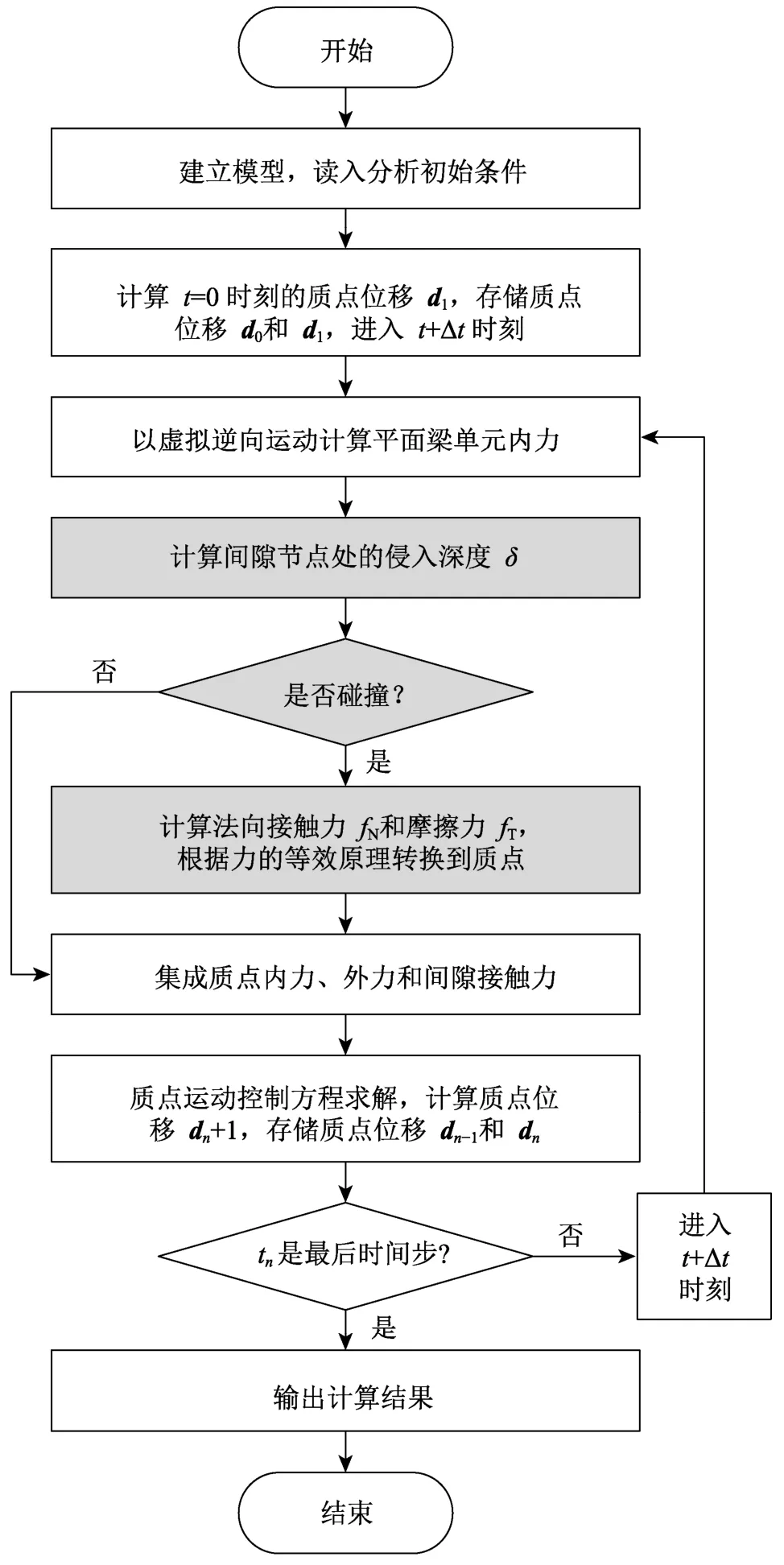
圖4 含間隙鉸平面機構的有限質點法計算流程Fig.4 Flowchart of finite particle method for planar mechanism with clearance revolute joint

3 數值算例

從上述分析和推導過程中可以看出，這種間隙鉸計算方法在已有的算法框架基礎上實現了間隙處的接觸偵測、接觸力計算和集成。本節通過算例驗證這種間隙鉸計算方法在平面機構動力分析中的有效性和穩定性。

3.1 平面四桿機構

本文首先對一個含間隙轉動鉸的平面四桿機構進行模擬。如圖5所示，此機構包含驅動桿、連桿和隨動桿，整個機構包括3個理想轉動鉸，分別連接驅動桿與支座、驅動桿與連桿、隨動桿與支座，而隨動桿與連桿之間為含間隙轉動鉸。機構各構件的特性見表1，間隙鉸的模擬參數見表2。構件截面尺寸選取方式如下：設構件的密度為ρ，質量為m，長度為l，質量慣性矩為I，則構件截面面積A=m/(ρl)，截面慣性矩為Iz=(I/ρl)，因此滿足截面面積A和截面慣性矩Iz的截面均可選為算例尺寸。本算例構件選用矩形截面，寬和高見表1。

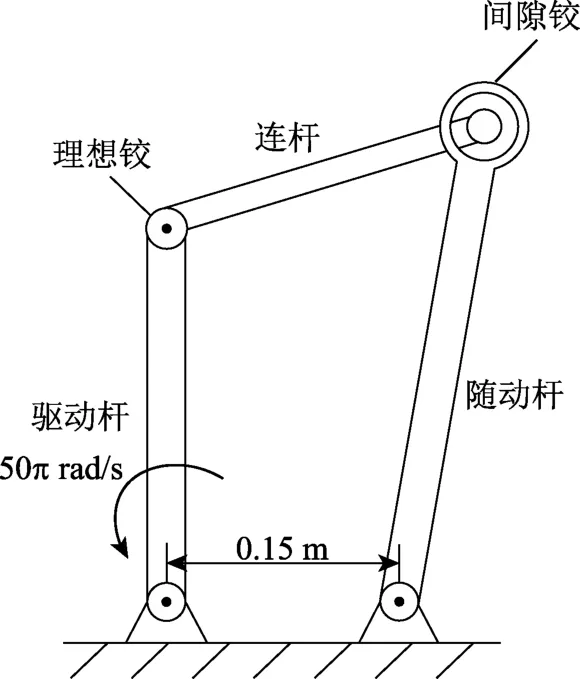
圖5 含間隙鉸的平面四桿機構Fig.5 Planar four-bar mechanism with clearance joint

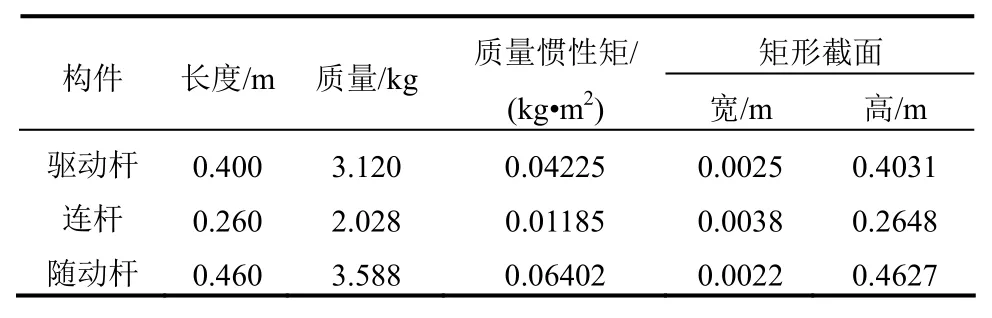
表1 四桿機構各構件的特性Table 1 Properties of each component in four-bar mechanism

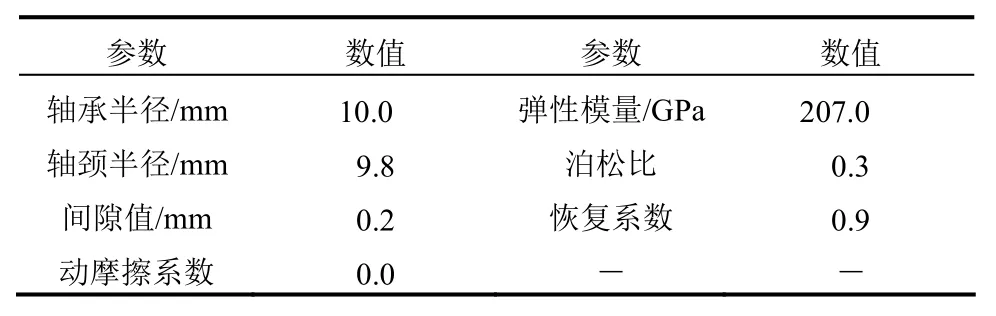
表2 四桿機構中間隙鉸的模擬參數Table 2 Simulation parameters for clearance joint in four-bar mechanism

采用有限質點法，將該機構各構件分別離散為5個質點和4個平面梁單元。為模擬剛性構件，梁單元的彈性模量可取相對較大的值。理想鉸處兩個質點之間的作用力通過上述位移耦合模型進行計算，間隙鉸處兩個質點的作用力通過上述間隙接觸模型進行計算。在初始狀態，驅動桿與地面垂直，初始角位移與角速度均為零。在驅動桿支座端施加逆時針強迫角位移以模擬驅動力，穩定后的角速度為50 π rad/s。為減小突加荷載引起的振動，首先進行0.12 s的線性加載，使驅動桿的速度從0線性增加至50 π rad/s。之后的計算總時間為0.14 s，積分時間步長為10-7s。

為考察間隙對機構動力響應的影響，本文首先對全為理想鉸節點的平面四桿機構進行分析，然后將連桿和隨動桿之間的鉸節點改為間隙鉸節點進行分析。圖6(a)和圖6(b)分別繪制了一個運動周期內(驅動桿角度為0°～360°)隨動桿的角速度和角加速度的時程曲線。從圖中可以發現，間隙的存在對隨動桿角速度的影響不大，但對其角加速度有較大影響。在角速度達到峰值的時刻附近，含間隙鉸的機構角速度有一定的波動，對應的角加速度曲線劇烈振蕩，其最大值相對于理想鉸機構有較大增加。圖6(c)繪制了間隙鉸處的接觸力，可以發現當驅動桿角度為250°～270°時，間隙鉸的接觸力劇烈震蕩。為考察間隙鉸對動力效應的影響，分別定義隨動桿角加速度和間隙接觸力的放大系數DEα和DEF：

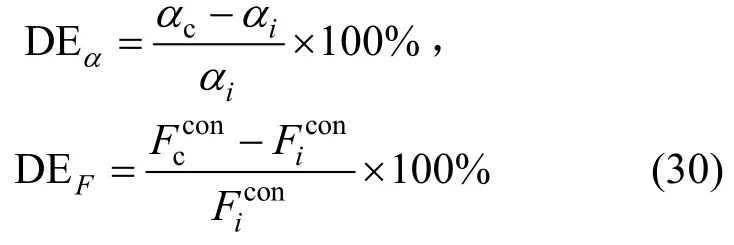
式中：αi和αc分別為理想鉸機構和含間隙鉸機構中隨動桿的最大角加速度；分別為理想鉸機構和含間隙鉸機構中接觸力最大值。從圖6(b)和圖6(c)分別提取角加速度和接觸力的最大值，可以得到DEα和DEF分別為66.9%和16.6%。從圖6(c)可以看出，在驅動桿角度為0°～225°時，理想鉸接觸力振動略大于間隙鉸接觸力，其原因為：驅動桿作用力通過平面梁單元傳遞給質點，而梁單元內力也存在一定程度的振動；本文方法中的質點運動方程采用牛頓第二定律求解，質點在梁單元內力作用下也表現為圍繞平衡點進行一定幅度的振動，但其振動不影響計算結果的收斂性。理想鉸機構中，沒有耗能的阻尼項，從而振動沒有被消除；含間隙鉸機構中，接觸力中的耗能阻尼項減小了接觸力的振動，從而接觸力曲線較平滑。

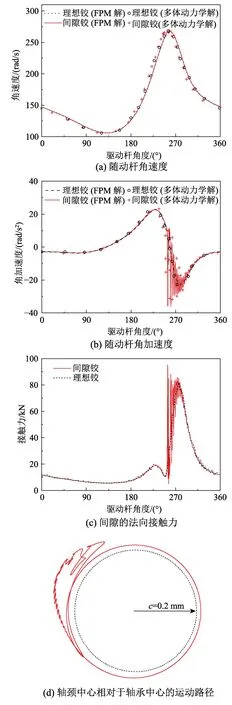
圖6 含間隙鉸的平面四桿機構模擬結果Fig.6 Simulation results for planar four-bar mechanism with clearance joint

通過跟蹤機構運動的全過程可知，在運動初期，軸頸和軸承出現分離現象，隨后軸頸與軸承始終保持接觸狀態。圖6(d)繪制了穩定周期運動下軸頸中心相對于軸承中心的運動路徑，可以看出侵入深度δ＞0，說明軸頸和軸承保持接觸狀態。δ在一個周期運動中的某段時間內增大，表明對應的法向接觸力達到峰值。以上分析結果與文獻[19]中采用多體動力學方法分析的結果一致，證明了有限質點法用于處理間隙轉動鉸的正確性。

3.2 曲柄滑塊機構

為驗證本文方法在柔性機構及含多個間隙鉸機構的動力問題求解方面的適用性，采用本文方法對一含間隙鉸的曲柄滑塊柔性機構進行動力模擬。

如圖7所示，此機構包含驅動桿、連桿和滑塊，滑塊可在水平方向自由滑動。整個機構包括兩個理想轉動鉸，分別連接驅動桿與支座(鉸1)、驅動桿與連桿(鉸2)，連桿與滑塊之間為含間隙轉動鉸(鉸3)。柔性連桿在驅動力作用下將發生彎曲變形。機構各構件的特性見表3，間隙鉸的模擬參數見表4。

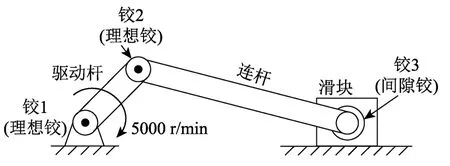
圖7 含間隙鉸的曲柄滑塊機構Fig.7 Slider-crank mechanism with clearance joint

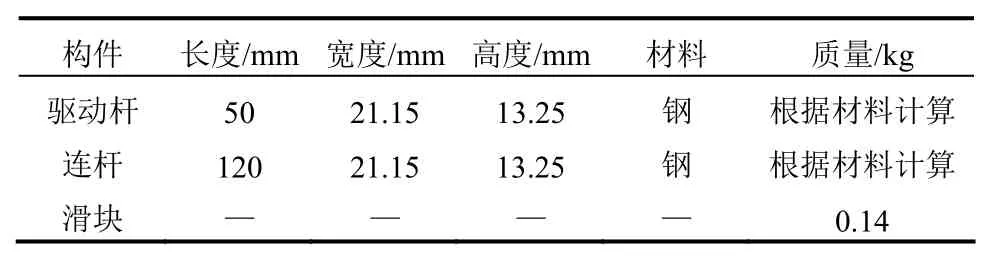
表3 曲柄滑塊機構各構件的特性Table 3 Properties of each component in slider-crank mechanism

表4 曲柄滑塊中間隙鉸的模擬參數Table 4 Simulation parameters for clearance joint in slider-crank mechanism

采用有限質點法，將驅動桿離散為2個質點和1個平面梁單元，將連桿離散為5個質點和4個平面梁單元。滑塊以獨立質點模擬，其質量通過質點的集中質量形式施加，并約束該質點的豎向線位移和角位移，以模擬滑塊的約束條件。理想鉸和間隙鉸的模擬方法與平面四桿機構的算例相同。在初始狀態，驅動桿與地面平行，初始角位移與角速度均為零。在驅動桿支座端施加順時針強迫角位移以模擬驅動力，穩定后的角速度為5000 r/min。為減小突加荷載引起的振動，首先進行0.024 s的線性加載，使驅動桿的速度從0線性增加至5000 r/min。之后的計算總時間為0.096 s。考慮機構中連桿分別為剛性和柔性兩種情況，其彈性模量分別取2.07×1013Pa和2.07×1011Pa 。根據式(5)，積分時間步長分別取為1.59×10-7s和4.2×10-7s。

圖8(a)～圖8(b)對比了理想剛性機構、含間隙鉸剛性機構和含間隙鉸柔性機構的動力響應，并分別繪制了兩個運動周期內(驅動桿角度為0°～720°)滑塊的速度和加速度的時程曲線。可以看出，含間隙鉸剛性和柔性機構的動力響應振動幅度和峰值均比理想剛性機構的動力響應大。相對于含間隙鉸剛性機構，含間隙鉸柔性機構的速度和加速度振動幅度要小一些。從圖8(c)可以看出，含間隙柔性機構的接觸力峰值也比含間隙剛性機構要小約40%。以上結論與文獻[20]的試驗結果相符。圖8(d)還繪制了間隙鉸中軸頸中心相對于軸承中心的運動路徑，可以看出運動過程均經歷了自由運動、碰撞和接觸三種狀態，但柔性機構中軸頸的相對運動路徑更不平滑。從圖示結果可以看出，本文方法和文獻[7]通過理論推導和分析得到的結果一致，驗證了本文方法在求解含間隙柔性機構動力問題的適用性。

為進一步驗證本文方法在求解多間隙鉸機構動力問題的有效性，將本算例中驅動桿和連桿之間的轉動鉸(鉸2)也設為含間隙鉸，比較理想鉸、單個間隙鉸和多個間隙鉸柔性機構的動力效應。圖9(a)～圖9(c)繪制了多個間隙鉸機構的滑塊速度、加速度以及間隙接觸力的時程曲線。相比單個間隙鉸，多個間隙鉸機構中滑塊速度的峰值有所增大，同時峰值處相位滯后更為明顯；同時，多間隙鉸機構中加速度和接觸力峰值均有較大幅度增加。以上結果說明多個間隙鉸將顯著增加機構的動力響應。圖9(d)繪制了軸頸中心相對于軸承中心的運動路徑，相對于單間隙鉸機構，多間隙鉸機構中的鉸3自由運動狀態的幅度和范圍更大，而鉸2主要以接觸狀態為主。

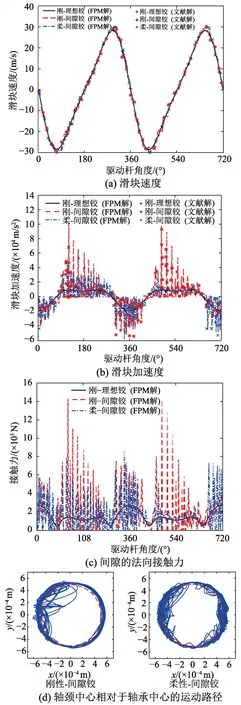
圖8 含單個間隙鉸的曲柄滑塊機構模擬結果Fig.8 Simulation results for slider-crank mechanism with single clearance joint

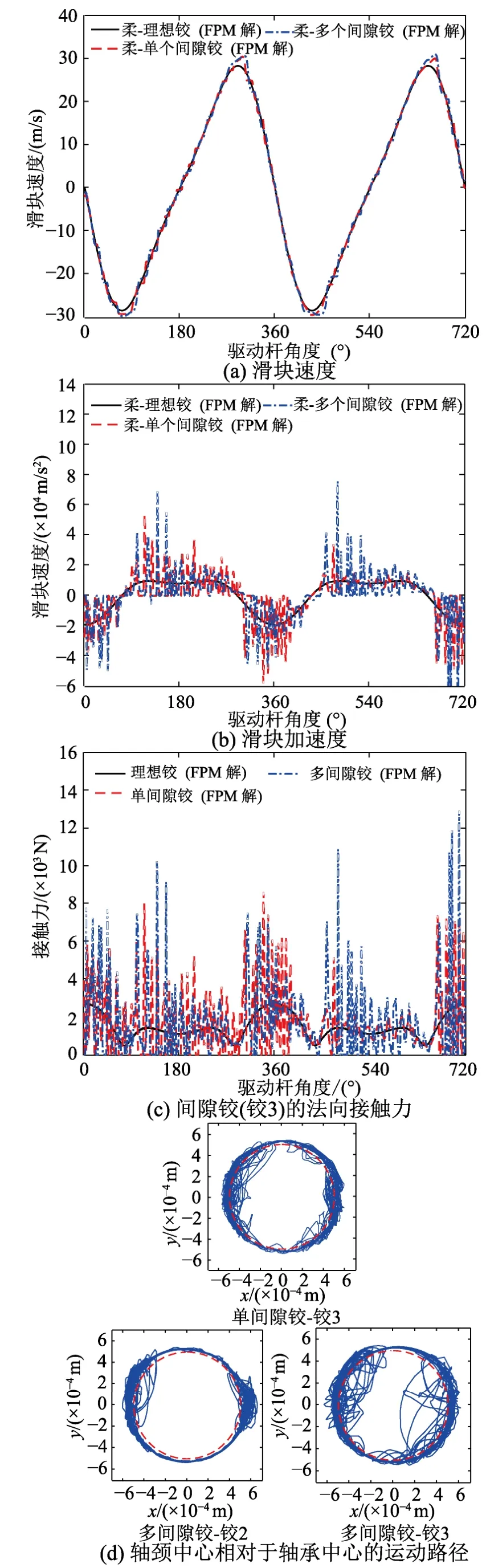
圖9 含多個間隙鉸的曲柄滑塊機構模擬結果Fig.9 Simulation results for slider-crank mechanism with multiple clearance joints

從本算例可以看出，本文方法不需進行復雜的理論推導，適合用于建立各種復雜機構模型；在進行剛性和柔性機構分析時，只需調整構件的彈性模量即可；同時適用于多間隙鉸機構動力分析，編程簡單方便，適用性強。

4 結論

有限質點法不需要集成整體剛度矩陣，適合進行機構動力分析，質點間作用力的處理也十分方便。本文基于有限質點法，建立了含間隙鉸平面機構的動力分析方法，算例表明本文方法是正確并有效的，建模直觀，編程簡單方便，并且適用于求解含多個間隙鉸的柔性機構動力問題。值得說明的是，其他的接觸力和摩擦力模型在本文提出的計算框架下實現起來也非常容易。利用本文方法對平面四桿機構和曲柄滑塊機構進行了動力分析，結果表明間隙鉸對機構運動的位移和速度影響不大，但會使機構的加速度和間隙鉸的接觸力有較大振蕩。利用本文提出的間隙鉸分析方法，可在實際工程中考慮間隙對復雜機構或含機構運動的結構進行分析，從而評估間隙產生的動力效應，為機構或結構設計提供指導。