考慮剪切作用的盾構隧道管片接頭力學模型研究

耿 萍，唐 睿，陳枰良，郭翔宇，何 川，張艷陽

(西南交通大學交通隧道工程教育部重點實驗室，四川，成都 610031)

盾構隧道是由螺栓將管片連接而成的地下結構。大量研究表明，盾構隧道接頭是結構的薄弱部位[1]，易受到地震、地層變形、施工和運營荷載等的影響[2－3]，其力學行為對襯砌結構受力特征有重要影響[4－7]。

針對管片接頭，通常使用理論解析和加載試驗的方法來研究其力學特征。在管片接頭試驗方面[8－14]，大多是以原型管片或局部接頭加載試驗為基礎，對管片接頭接縫面混凝土受力、螺栓受力及接縫張開量等進行研究。在管片接頭理論解析方面，村上博智、小泉淳[15－17]通過假定接縫面混凝土受壓區壓力分布形式，包括矩形、拋物線形、三角形等，從而推導管片接頭的力學模型[18－20]；張建剛和何川[21]提出了考慮管片接頭處襯墊和端面混凝土共同變形的改進分層條帶算法，從而推得管片接頭力學模型；陳三江等[22－24]將接縫面混凝土視為剛性，不考慮變形，從而得到與連接螺栓、襯墊等形成的彈簧-剛性板模型；張冬梅等[25]將管片間的相互作用離散為一系列彈簧的組合，通過動態調整彈簧參數，計算接頭的內力及張開量。此外還有學者[26]通過試驗得到的大量數據樣本，采用擬合的方式得到管片接頭力學模型。

無論是試驗還是理論模型，可以發現，管片接頭受到軸力、彎矩和剪力三種力的共同作用。同時，由于接觸的存在，管片接頭接縫在軸向、彎曲及剪切三個方向上的力學性質會相互影響。但現有研究大多視切向為剛性，聚焦于接頭的抗彎性能和接頭張開量，一般僅考慮軸力與彎矩共同作用，使得考慮剪力作用下的管片接頭解析模型較為匱乏。而當剪切力存在時，剪切作用使得接頭位置或出現剪切位移，接縫處結構的接觸狀態變得更為復雜，以往基于接頭切向為剛性這一假定而推導的接頭力學模型或將不再適用。所以，考慮剪切作用對完善盾構隧道管片接頭力學模型具有一定意義。

本文首先對盾構隧道管片接頭的力學建模問題進行了界定，以位移為已知量，推導了考慮剪切作用下的管片接頭力學模型，并參考既有的獅子洋盾構隧道工程，采用有限元法對該力學模型進行了驗證。

1 考慮剪切作用的管片接頭耦合力學模型

1.1 管片接頭力學建模的基本問題

如圖1所示，由于管片接頭力學行為對管片受力的影響范圍有限，這里假定受接頭影響的區域的兩側邊界為邊界1和邊界2(圖1中邊界位置僅為示意)，本文所討論的管片接頭力學問題即在接頭影響區域內，如何將管片結構及螺栓在三方向上(軸向、轉動、切向)的受力與變形位移通過力學關系式聯系起來。

將管片接頭影響區內的接頭結構截出，如圖2所示，這里是以斜螺栓為研究對象。為便于理論推導，假定螺栓兩側端頭與結構混凝土的變形在同一剛性端面上，端面上螺栓與結構混凝土產生相同位移。接頭主要影響兩端面內區域，對以外的區域影響不大，故可按照梁結構對端面外區域進行分析。此時，當位移作為已知荷載時，即可分開推導螺栓與結構混凝土的力學模型，使問題簡化。由于接頭影響區域曲率很小，可以將此區域簡化為直線。

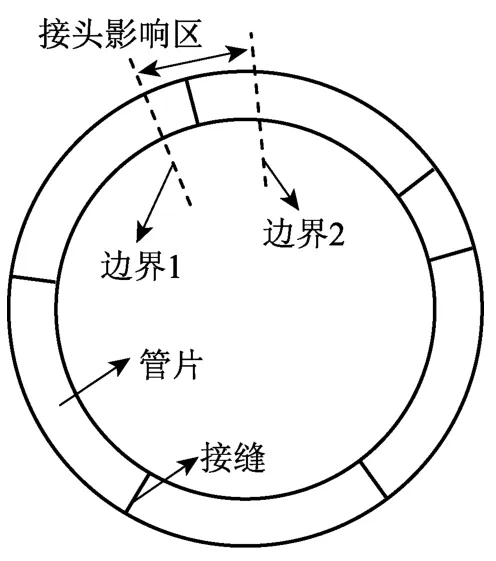
圖1 盾構隧道管片接頭影響范圍Fig.1 Influence area of segment joint

圖2 管片接頭力學結構模型Fig.2 Mechanical model of segment joint

接頭影響區域軸向、轉動及切向這幾個方向上位移與力的關系，用式(1)表示。

式中：N1，V1，M1，N2，V2，M2分別表示左右兩剛性端面上傳遞的軸力、剪力和彎矩；u1、v1、θ1、u2、v2、θ2分別表示左右兩剛性端面上的軸向、切向和轉動位移；kij(i,j= 1,2,…,6)為各自由度間的剛度系數。本文的目的是確定式(1)中的剛度系數，從而建立盾構隧道管片接頭耦合力學模型。

1.2 接頭耦合力學模型建立

圖3為研究區域的螺栓及管片結構分析圖，其中，x軸為分析區軸線，y軸位于左端面內。hj為斜螺栓右端至x軸的垂距。hf為x軸至研究區域頂面的距離，即研究區域高度的一半。α為斜螺栓與x軸的夾角，正向為順時針向。lz、l分別為接縫面、右端面與左端面間距。考慮到推導時施加位移荷載的方便，約束左端面，在右端面施加相對位移，按式(2)～式(4)進行計算。

圖3 接頭結構受力分析圖Fig.3 Analyzing diagram of joint structure

推導過程分為螺栓力學方程的推導和考慮剪力下管片結構力學方程的推導兩個部分，在求出各自的控制方程后合成總的剛度矩陣，得到考慮剪切作用下的管片接頭耦合力學模型。

1.2.1 螺栓力學方程

右端面上螺栓端頭的位移為：

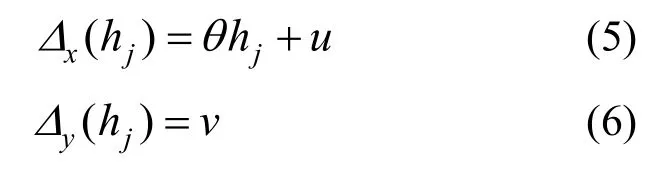
將螺栓端頭作為原點構建局部直角坐標系，如圖3所示，n軸代表軸向，t軸代表切向。則在該坐標系下，螺栓端頭的變形為：

式中，Δjn、Δjt分別表示軸向與切向這兩個方向上的變形。

由此螺栓受力可表示為：

式中：Fjn和Fjt分別為螺栓所受軸力與剪力；與之對應的kjn和kjt分別為軸向和切向剛度，可通過對螺栓變形-力曲線作割線獲得，如圖4表示。P為螺栓預緊力；圖4中dn和dt分別為兩個方向上的變形量。

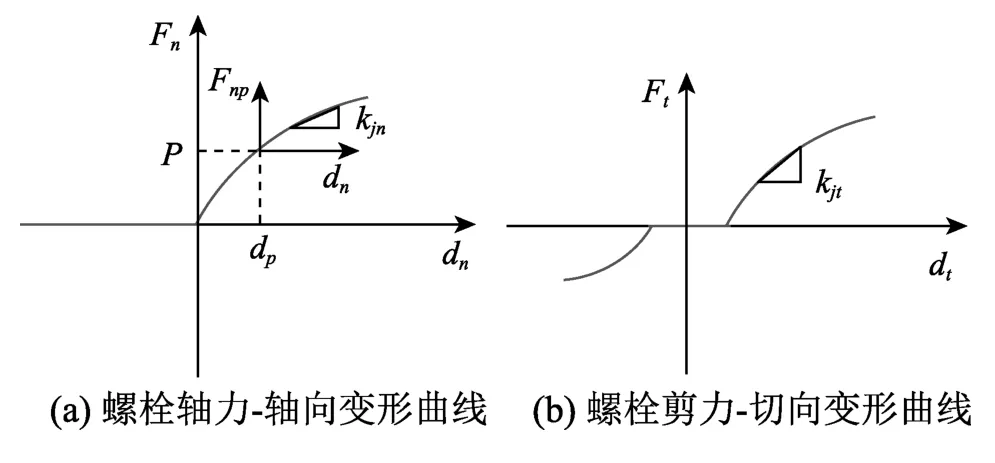
圖4 螺栓變形曲線Fig.4 Bolt’s deformation curves

右端面各方向的作用力為：

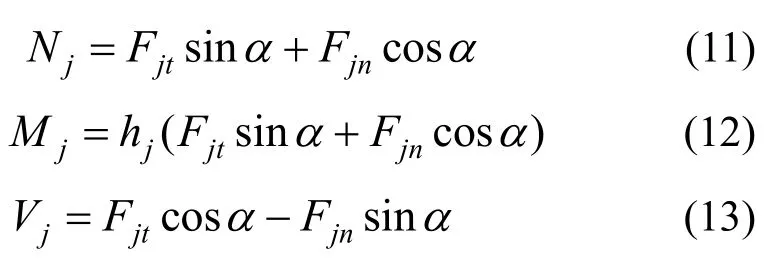
將Fjn和Fjt代入，并寫為矩陣形式為：

其中：

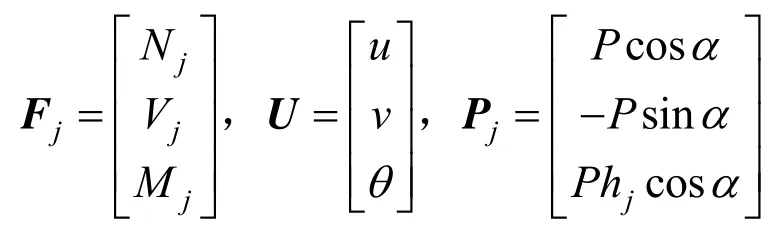
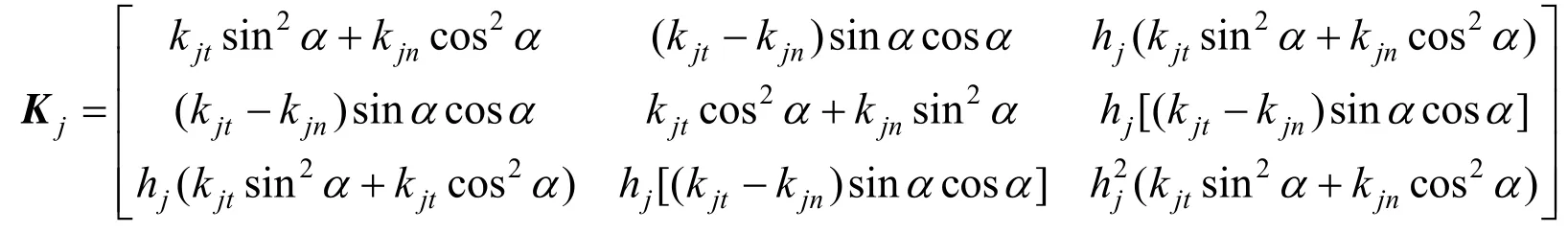
1.2.2 考慮剪切的管片結構力學方程

對于管片結構，可在先推導無剪力作用的情況后，再考慮剪力作用，然后進行疊加合成。無剪力作用情況即彎曲與軸向變形，如圖5所示。分別求解兩種情況下的結構混凝土力學方程，然后進行合成，即可得到考慮剪切的管片結構力學方程。

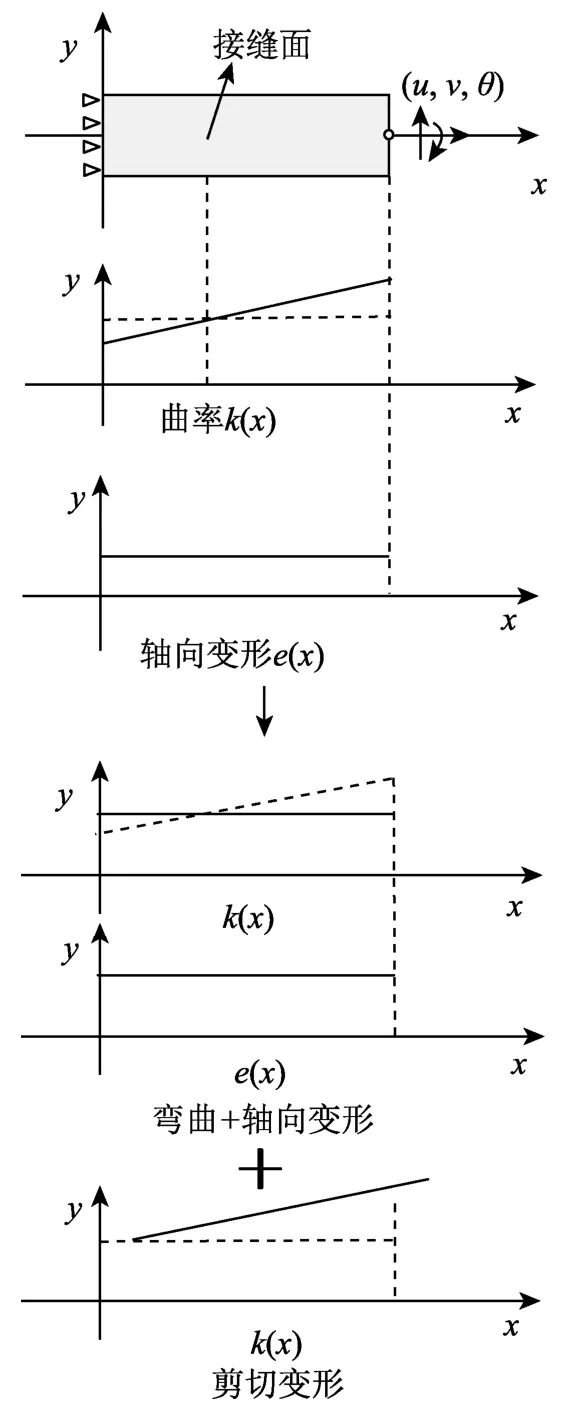
圖5 管片結構變形的分解Fig.5 The deformation decomposition of segment

1) 彎曲與軸向變形下管片結構力學方程

于右端面施加軸向、切向和轉動三個方向的位移，同時軸向位移u為0。若按梁考慮兩端面內的管片結構，則端面內區域軸線上各位置的撓度可通過式(15)計算：

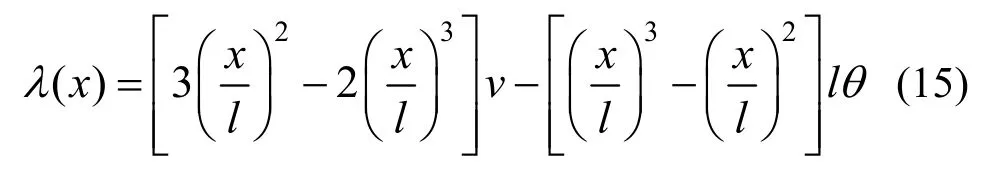
對式(15)求一階及二階導，可以得到區域內各個截面較左端面(被固定約束)的相對轉角θ(x)和各截面軸向的曲率k(x)。當無剪力作用時，各截面軸向的曲率應相同，即：

求得：

說明當切向位移v滿足式(17)時，管片結構中無剪力傳遞，不滿足則存在剪力。

無剪力作用時，各截面軸線的軸向曲率為：

此時再考慮位移u，則研究區的軸線在軸向上的變形可通過式(19)表示：

對式(19)求導，可得到對應的應變：

對接縫面而言，其轉角變化率即曲率k，如圖6所示。則接縫面處受拉、受壓區分界位置的坐標可通過軸向變形率e與曲率k之比表示：

式中，ho正負方向與y軸正負方向相同。

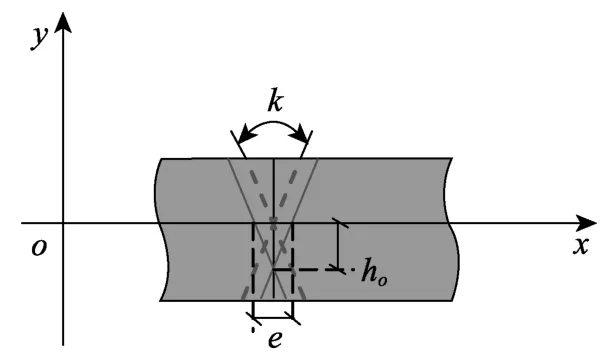
圖6 接縫面不同接觸形式劃分Fig.6 Different kinds of contact in joint surface

對接縫的接觸形式，可通過分界坐標和軸向位移進行判定：

① 當u＞ 0，ho≥hf或ho≤-hf，無接觸。

② 當u＜ 0，ho≥hf或ho≤-hf，全接觸。

③ 當u≥0,0 ＜ho＜hf或u＜ 0，-hf＜ho＜ 0，上部接觸。

④ 當u≥0,-hf＜ho＜ 0或u＜ 0，0＜ho＜hf，下部接觸。

于是，接縫面上的應變函數為：

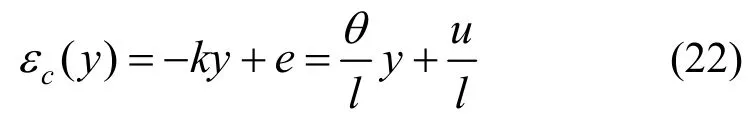
接縫面無法傳遞拉力，故式(22)為負值或為0。于是，右端面各自由度的作用力為：

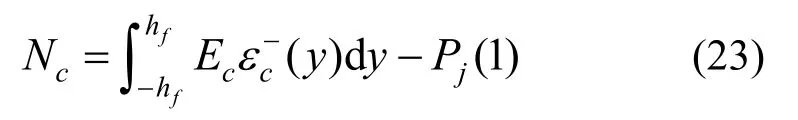
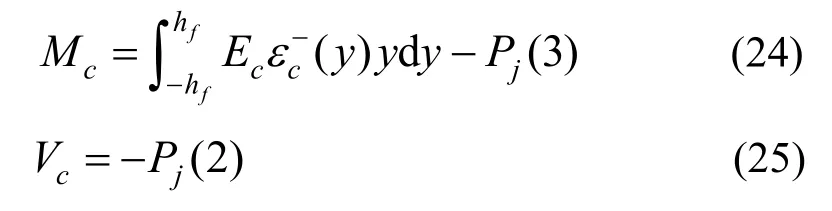
式中：Ec為結構混凝土的彈性模量；Pj為式(14)存在的螺栓預緊力項。

對式(23)～式(25)分別進行積分。對不同接觸狀態，可以用一個總的矩陣表示，如式(26)所示。

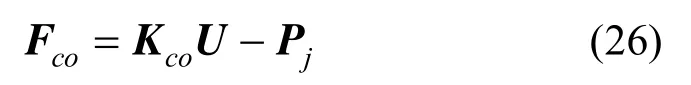
其中：

式中：對接縫不同的接觸狀態，Ax為該接觸狀態下，接縫接觸區域截面的面積；Sx、Ix分別為該接觸狀態下接縫區相接觸的截面對截面形心的靜面矩和慣性矩。

2) 剪力作用下的管片結構力學方程

當考慮剪力作用時，先求出右端面上作用有u、v、θ三個方向的位移下，無剪力作用狀態(即彎曲和軸向變形)引起的位移。此時接縫面處有：

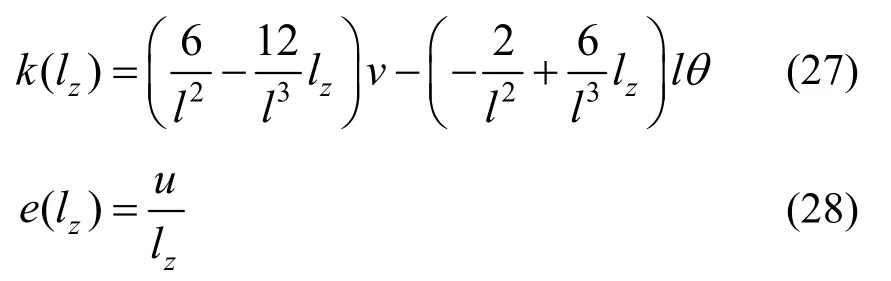
由于軸向變形僅在無剪狀態下產生，故該狀態下的軸向位移為：

同時，無剪狀態下，接縫面處曲率k(lz) =k，故該狀態下右端面的轉角為：

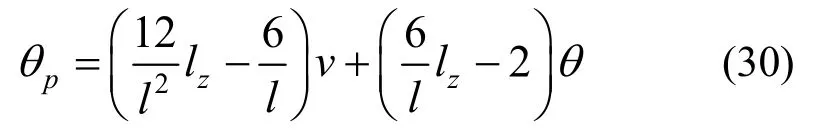
將式(17)代入，得該狀態下右端面上的切向位移：

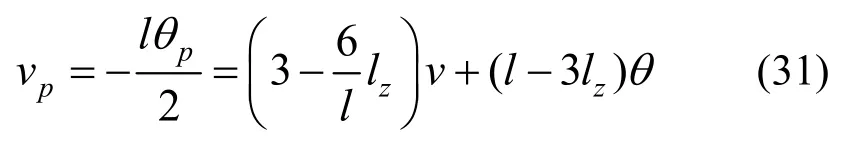
則用右端面的總位移減去彎曲與軸力引起的位移即可得到剪力作用引起的位移：

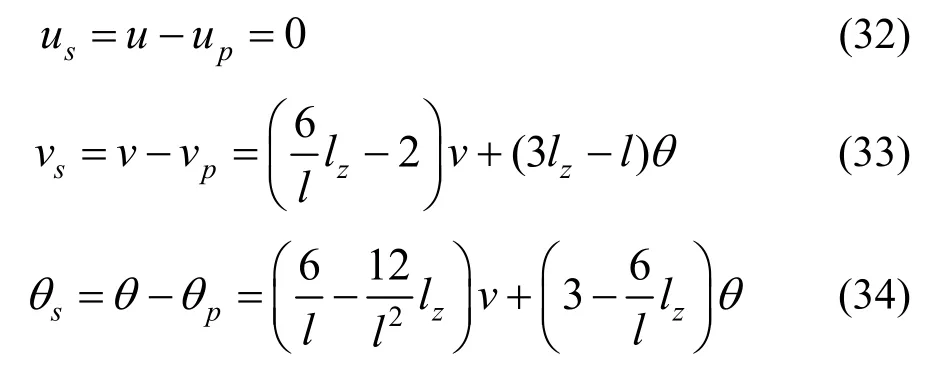
對無剪切作用部分，有：

將式(30)和式(31)代入式(35)可得：

其中：

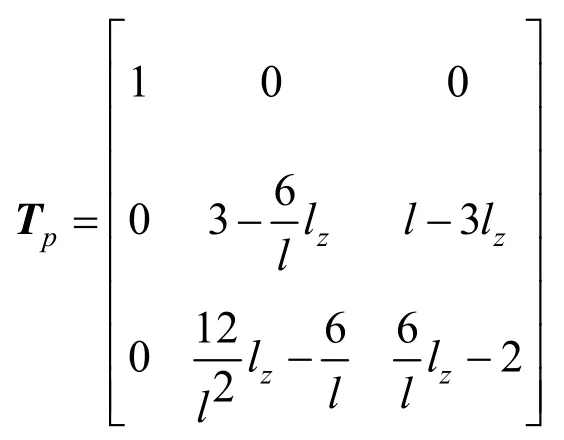
而對有剪切作用部分，按一般梁考慮，則對應力學方程可按式(37)表達：

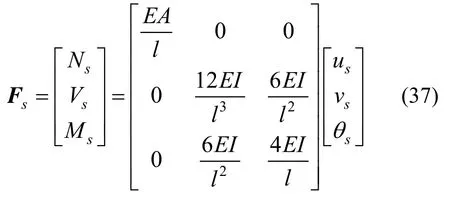
將式(32)～式(34)代入式(37)可得：

其中：

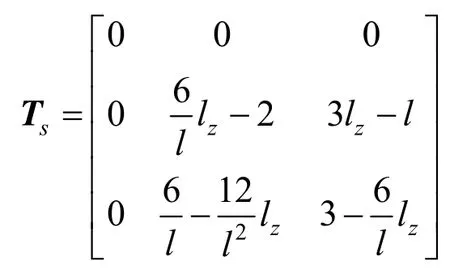
將彎曲與軸向變形部分和剪力作用部分合并，同時考慮螺栓預緊力，則管片結構的力學方程可表示為：

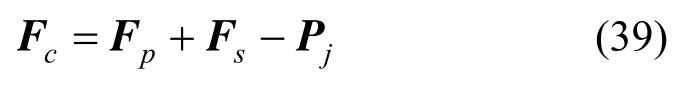
代入得：

其中，若令ξ= lz / l，上式中：

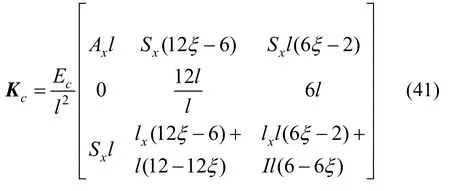
1.2.3 剛度矩陣合成

由于螺栓與管片結構共同受力，則右端面處總的作用力可以按式(42)表示：

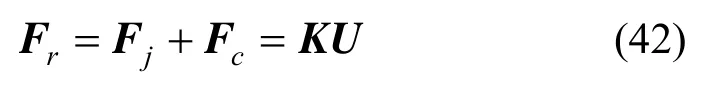
其中：

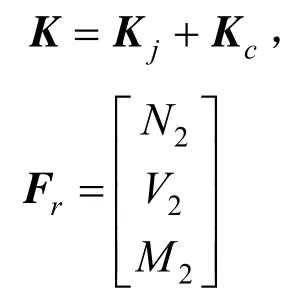
式(42)中的剛度系數可用式(43)表示。此時約束左端面，通過受力平衡條件即可推得含有左端面反力的力學方程，即式(44)。

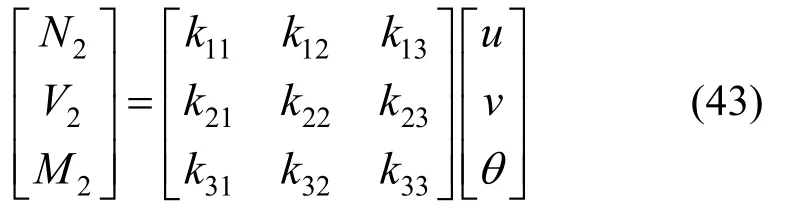
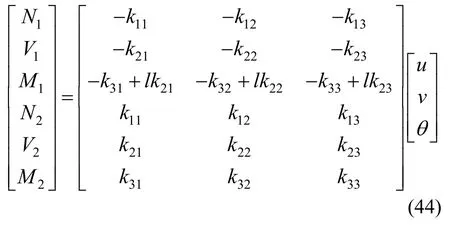
將式(2)～式(4)代入式(44)，即可得到左右端面都有位移產生時的力學方程：

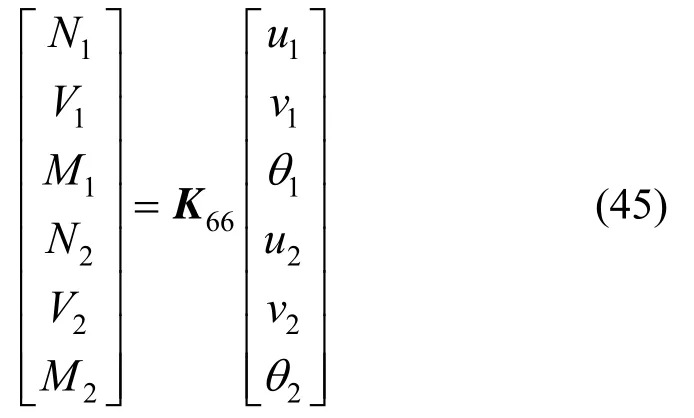
其中，K66為：

K66剛度陣各元素即為式(1)的對應各參數。之后，通過代入兩側端面上的位移矩陣[u，v，θ]或者力矩陣[N，V，M]，通過剛度矩陣，即式(1)，即可求解管片接頭的受力、位移狀態。

2 管片接頭耦合力學模型驗證

2.1 工程概況

獅子洋盾構隧道采用了C50混凝土，每環均布22顆縱向螺栓，使用“7+1”的分塊方式。環向螺栓為斜螺栓，等級M36，與管片軸向呈30°角。隧道橫斷面結構形式見圖7，B1～B5為標準管片，L1～L2為鄰接塊，F為封頂塊，管片圓心角及縱向螺栓布置角度如圖7所示。

2.2 接頭模型驗證

2.2.1 有限元法數值模型建立

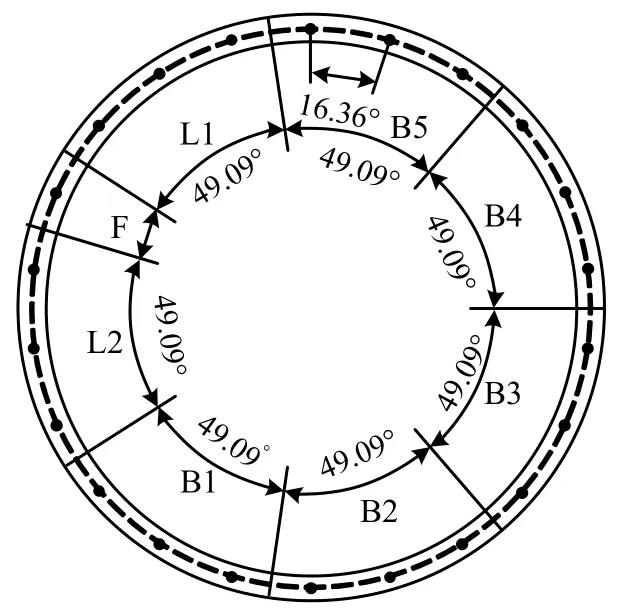
圖7 獅子洋盾構隧道橫斷面結構圖Fig.7 The structural diagram of Shizi Yang Shield Tunnel in transverse section

建立如圖8所示有限元法模型。左面采用固定約束，三個方向上的位移荷載均施加于右面。荷載的取值范圍根據既有研究確定[27]，其中u為?0.05 mm～0.05 mm，v為?0.5 mm～0.5 mm，θ為-0.0016 rad～0.0016 rad。對不同位移荷載組合工況進行計算，并記錄模型右端中心節點處的N、V、M。

2.2.2 計算模型驗證

1) 軸力N

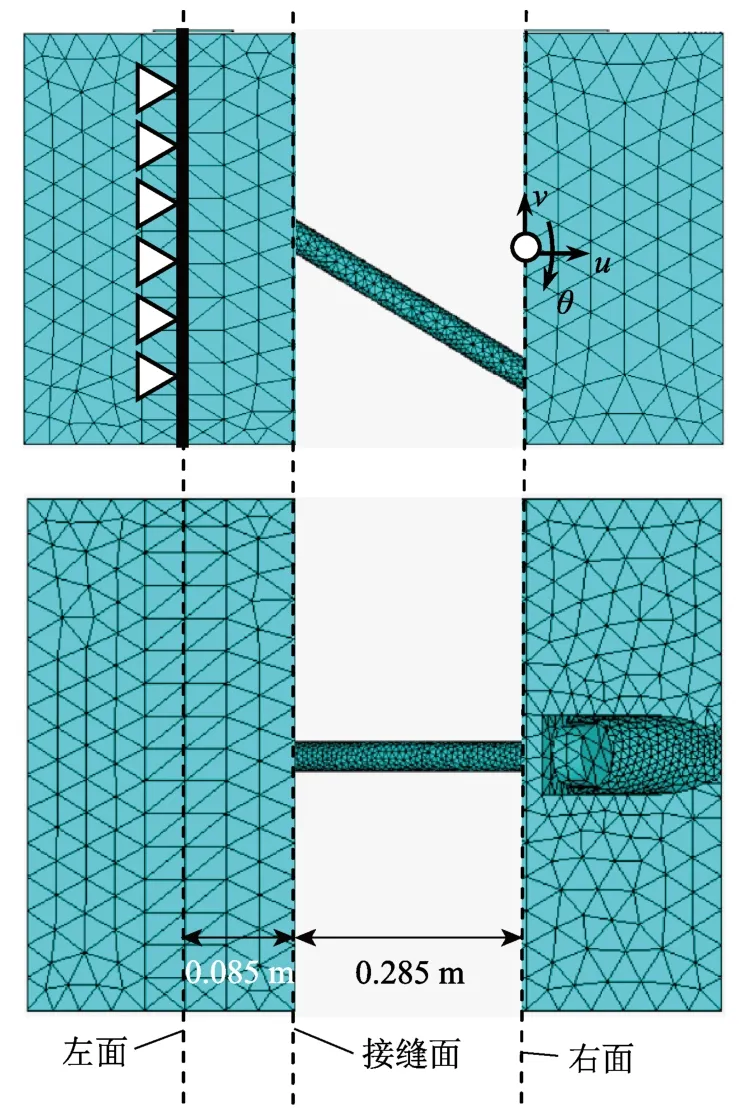
圖8 接頭有限元模型Fig.8 Joint model by finite element method

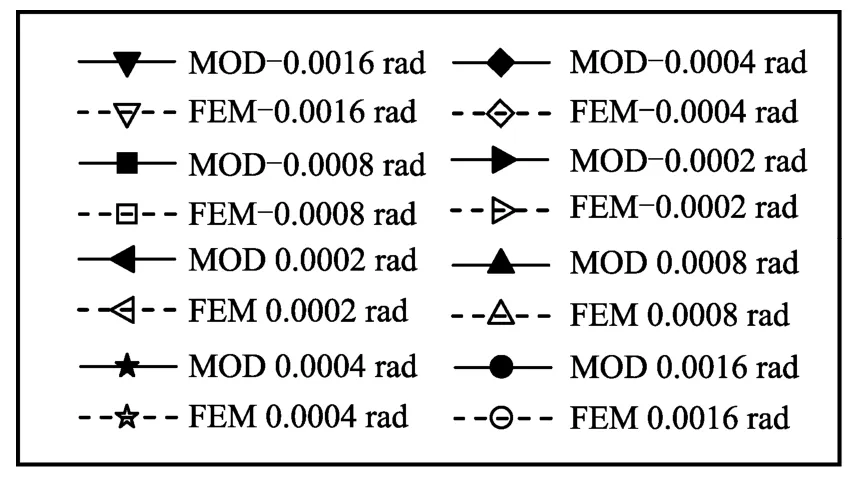
圖9 計算圖例示意圖Fig.9 Figure of the legend

為便于說明，圖9為圖例示意，FEM代表有限元法，MOD代表本文推導的計算模型。之后的剪力、彎矩均使用相同的圖例。圖10為兩種方法計算下的軸力N在各工況下的變化情況。可以看出，有限元法與本文提出的計算模型計算得到的規律吻合較好：軸向位移和轉動位移條件固定時，切向位移對軸力的變化略有影響；軸向位移與切向位移條件固定，軸力隨轉動位移的增大而增大；轉動位移與切向位移條件固定，隨著軸向位移的增大，軸力逐漸減小。

對軸力而言，本文提出的模型(后簡稱“模型”)的計算結果較有限元法大。當剪切位移趨近于0時，兩種方法的結果差別較小，此時相當于本文提到的無剪力作用情況。

2) 剪力V

圖11為兩種方法計算下的剪力V在各工況下的變化情況。兩種方法計算得到的規律大致相同：軸向位移和轉動位移條件固定，剪力對剪切位移的變化較為敏感，且隨剪切位移的增大而增大；軸向位移與切向位移條件固定，剪力隨轉動位移的增大而增大；轉動位移與切向位移條件固定，剪力隨軸向位移增大而略微減小。

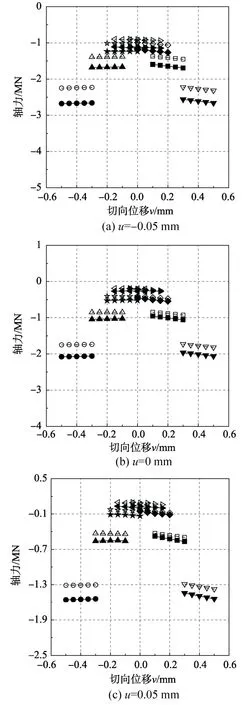
圖10 不同計算工況下的軸力變化Fig.10 Tension varies under the different working conditions

此外，在相同軸向位移與轉動位移條件下，存在某一剪切位移值，該值下兩種方法的計算結果差別較小，而偏離該值后，差別增大。當軸向位移為負值時，兩種方法的結果差別較小。而隨著軸向位移向正值增大，兩者在剪切位移絕對值較小時差別較大。整體上模型得到的結果較有限元法稍小。

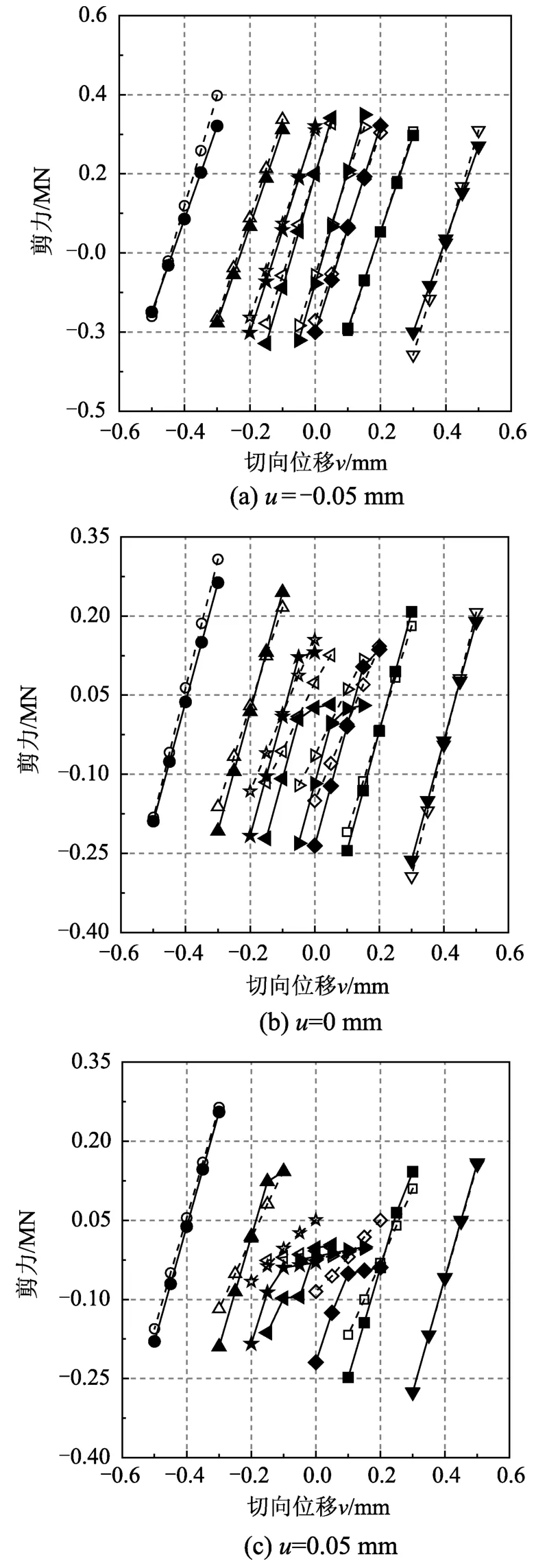
圖11 不同計算工況下的剪力變化Fig.11 Shear varies under the different working conditions

3) 彎矩M

圖12為兩種方法計算下的彎矩M在各工況下的變化情況。有限元法與本文模型的計算結果規律相吻合：軸向位移和轉動位移條件固定時，彎矩隨切向位移的增加而增大；軸向位移與切向位移條件固定，轉動位移越小，彎矩越小；轉動位移與切向位移條件固定，軸向位移越大，彎矩越小。

對比兩種計算方法，模型的計算結果比有限元法的計算結果稍大，但整體差別較小。

圖12 不同計算工況下的彎矩變化Fig.12 Moment varies under the different working conditions

3 結論

(1) 本文提出了一種管片接頭多自由度耦合力學模型的建立方法。位移作為已知量，分別對接頭研究區域內的螺栓和管片結構進行力學推導，得到各自的剛度矩陣。之后對剛度矩陣進行合成，得到接頭總剛度矩陣，從而建立考慮剪切作用的管片接頭耦合力學模型。

(2) 完成了考慮剪切作用下的管片接頭力學模型推導。推導了考慮剪切作用時螺栓的力學方程；對于管片結構，在推導管片結構在無剪力作用下的變形的基礎上，與剪力引起的變形進行疊加，得到考慮剪切作用時的管片結構力學方程。

(3) 以獅子洋盾構隧道為依托，采用有限元法對本文推求的模型進行了驗證。結果表明：在本文荷載范圍內，兩種方法所呈現的規律相同，具有良好的一致性；總體上，本文模型的計算結果稍大，以此結果為依據進行管片設計偏安全。

(4) 對比以往的研究[27-30]，本文建立的模型考慮了軸向、剪切及彎曲三個方向上荷載的耦合作用，使之更符合接頭的實際受力、變形情況。當求得接頭剛度矩陣后，即可較容易地計算管片接頭的內力或位移，便于工程應用。