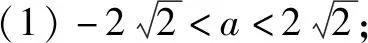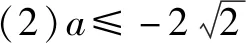恒成立問題的多角度思考

徐照武

(廣東省珠海市實驗中學(xué) 519090)

恒成立問題，覆蓋了函數(shù)、導(dǎo)數(shù)、不等式、三角、數(shù)列、解析幾何等高中數(shù)學(xué)的很多知識點，還涉及到一些重要的數(shù)學(xué)思想方法.多方位多角度歸納總結(jié)這類問題，對提高對恒成立問題的認(rèn)識及分析問題和解決問題的能力很有幫助.

一、恒成立溯源

這是一個古老問題，我們很少注意挖掘其來歷，其實它歷史悠久，來源于一元二次方程，這是我們很少注意到的.請看下面問題：

(1)已知方程2x2-ax+1=0無實根,求實數(shù)a的取值范圍.

(2)已知函數(shù)f(x)=2x2-ax+1>0對任意實數(shù)x都成立,求實數(shù)a的取值范圍.

(3)已知函數(shù)f(x)=-x3+ax2-x-1在R上是單調(diào)函數(shù),求實數(shù)a的取值范圍.

(1)是我們非常熟悉的一類題目，但若改為(2) (3)的敘述方式，實際就是恒成立問題.

二、高考試題中多次出現(xiàn)恒成立問題

1977年，恢復(fù)高考制度以來多次出現(xiàn)恒成立問題，如1990全國高考理數(shù)的壓卷題的第一問：

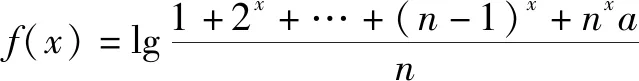
解析題目看似函數(shù)定義域問題，其實變換后是恒成立問題.

簡解f(x)當(dāng)x∈(-,1]時有意義的條件是：

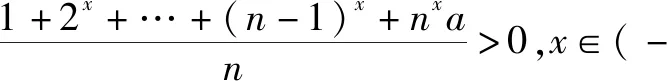
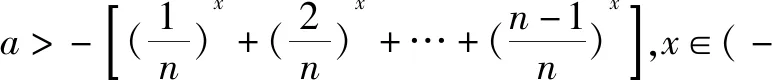
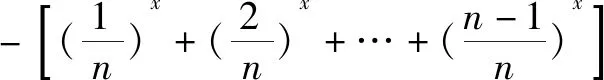
此題有一定難度.但可以說，以后的恒成立問題基本來源于此.

三、恒成立易錯的地方

例2已知對?x∈R,k≥sinx+cosx均成立，求k的最小值.

四、恒成立的分類及求解方法

1.a≥f(x)型

此類問題常利用最值法，即a≥[f(x)]max(如例2).

例4(2018全國一卷，選修4-5：不等式選講)已知f(x)=|x+1|-|ax-1|.

(1)當(dāng)a=1時，求不等式f(x)>1的解集；

(2)若x∈(0,1)時不等式f(x)>x成立，求a的取值范圍.

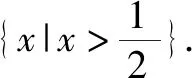
(2)當(dāng)x∈(0,1)時|x+1|-|ax-1|>x成立等價于當(dāng)x∈(0,1)時|ax-1|<1成立．

若a≤0，則當(dāng)x∈(0,1)時|ax-1|≥1；

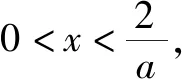
綜上，a的取值范圍為(0,2]．

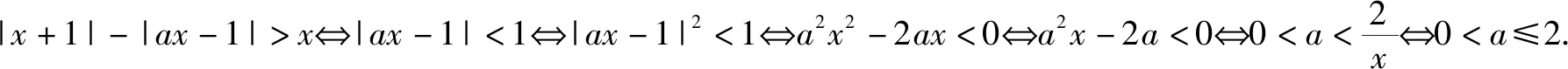
2.f(x，a)≥0型(即混合型)

一般有兩個途徑：分離變量轉(zhuǎn)化為a≥f(x)的形式，或利用[f(x,a)]min≥0求解.

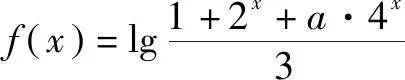
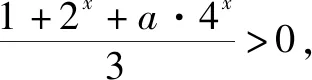
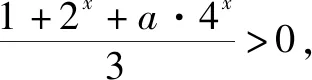
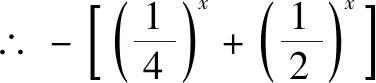
3.f(x，y)≥0型(即多變量型)

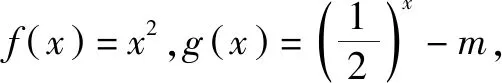
注：此類問題的條件?x1∈[-1,3]，?x2∈[0,2]可以有多種組合：?x1∈A,?x2∈B；?x1∈A,?x2∈B；?x1∈A,?x2∈B；?x1∈A,?x2∈B，因此就會有不同形式的題目.

例7(2012陜西理科21題(2))設(shè)函數(shù)f(x)=x2+bx+c(b,c∈R),若?x1，x2∈[-1,1]都有|f(x1)-f(x2)|≤4，求b的取值范圍.

分析與解此題即|f(x1)-f(x2)|的最大值≤4，而|f(x1)-f(x2)|的最大值就是f(x)在[-1,1]上最大值與最小值的差M.

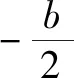
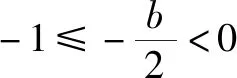
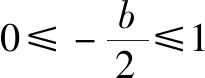
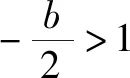
綜上可知：-2≤b≤2.

4.其它類型

下面一些學(xué)生熟悉的題目其實也是恒成立問題，只是我們平時不注意罷了.

(1)函數(shù)f(x)=lg(x2-ax+2)的定義域為R,求實數(shù)a的取值范圍.

(2)函數(shù)f(x)=lg(x2-ax+2)的值域為R,求實數(shù)a的取值范圍.

(3)函數(shù)f(x)=ax-1-1(a>0且a≠1)的圖象過定點____.

(4)直線x-ay+2a=0過定點____.

(5)12+22+32+…+n2=an3+bn2+cn+d對任意的正整數(shù)n都成立，求常數(shù)a,b,c,d的值.

(6)函數(shù)f(x)=-2x3+ax2+bx+c-1是奇函數(shù)，求實數(shù)a,c的值.