核心素養(yǎng)視野下學生數學彈性思維的培養(yǎng)

何正文

(廣東省肇慶市百花中學 526000)

筆者認為數學核心素養(yǎng)指的并不是一項特定簡單的數學能力,而是學生對于數學綜合能力的一個集合.而彈性思維就是學生數學核心素養(yǎng)基本要素，并且，彈性思維作為核心素養(yǎng)的重要品質進行體現(xiàn).數學彈性思維往往通過逆向形式，發(fā)散形式，類比形式，矛盾形式來進行深化核心素養(yǎng).

一、在逆向形式上培養(yǎng)學生彈性思維

逆向形式也叫反向彈性思維，因為思維慣性的原因，學生往往習慣著單一僵化的思維方向思考問題.如果能引導學生從結果進行出發(fā)，層層回推，找尋條件和相關定理，往往思路更為清晰.從這種逆向形式上往往能在縱向提高學生數學核心素養(yǎng)，強化培養(yǎng)學生彈性思維長度.

例如：已知矩形ABCD，過A作SA⊥平面AC，過A作AE⊥SB交SB于E，過E作EF⊥SC交SC于F.求證：AF⊥SC.

思路AF⊥SC?SC⊥含AF的平面AEF?SC⊥EF,SC⊥AE?AE⊥含SC的平面SBC?AE⊥SB,AE⊥BC?BC⊥含AE的平面SAB?BC⊥AB,BC⊥SA.

上面的解法是由結論到條件的逆向求解.

首先我們發(fā)現(xiàn)AF與SC是兩異面直線，要證明其垂直，往往要通過證明線面垂直，即證①AF⊥含SC的平面或證②SC⊥含AF的平面.因為題干中沒有給出與AF有關的垂直條件，學生的思維轉到證SC⊥含AF的平面AEF；繼續(xù)逆向思考，逆向證SC⊥平面AEF，根據線面垂直的判定定理，即證SC⊥EF,SC⊥AE；已知SC⊥EF, 目標變成要證SC⊥AE，SC與AE是兩異面直線，那么需考慮證明線面垂直,即證AE⊥含SC的平面SBC;逆向證AE⊥含SC的平面SBC,也就是證AE⊥SB,AE⊥BC；已知AE⊥SB，逆向證AE⊥BC，即證BC⊥含AE的平面SAB；逆向證BC⊥平面SAB，即證BC⊥SA,BC⊥AB；顯然BC⊥SA,BC⊥AB都是已知.在逆向思考中不斷排除干擾，與已知條件進行分析，逐層分析，從而得到問題解決.

二、在類比形式上培養(yǎng)學生彈性思維

類比是一種重要彈性思維培養(yǎng)方法，根據問題在某一方面的某種特定的性質判斷它們推導出在其他方面也存在著相同或者相似性質.這種類比形式往往能夠在橫向上提高學生數學核心素養(yǎng)，強化培養(yǎng)學生的彈性思維寬度.

例如：已知數列{an}、{bn}是兩個等比數列，那么

(1)數列cn=an·bn是否仍是一個等比數列呢？先特殊舉例分析，再進行證明.

(2)教師能類比提出問題.

①數列{an+bn}是否是等比數列？數列{an-bn}是否是等比數列？

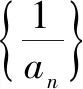
④數列{|an|}是否是等比數列？數列{can}是否是等比數列？(其中c為常數)

⑤在數列{an}中將下標成等差數列的項依次取出來組成一個新數列，這個新數列是否是等比數列？

又例如在講三角函數的單調性時，我們可以通過一組簡單的變式使學生加深對這個性質的理解：

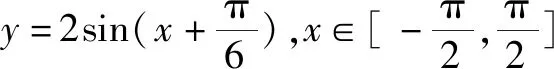
三、在發(fā)散形式上培養(yǎng)學生彈性思維

發(fā)散形式如同輻射出發(fā)，以一種不斷擴散形式出發(fā)思考，在某一個數學問題上，一題多解很適合運用這種培養(yǎng)思維方式，教師以這個問題為中心，從各個不同的知識點，不同形式的思考方式展開思考的方向，不斷發(fā)散，不滿足只找一個正確的答案.從發(fā)散形式上分散性上提高學生數學核心素養(yǎng)，強化培養(yǎng)學生彈性思維厚度.

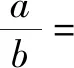
解法一由正弦定理

sinBcosC+sinCcosB=2sinB，

化簡得a=2b，

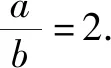
解法三由三角形射影定理，知bcosC+ccosB=a，

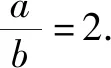
故填2.

四、在矛盾形式上培養(yǎng)學生彈性思維

矛盾不是數學定理概念本身、也不是題目已知條件，它是一種思維方式不同產生的，學生在矛盾中發(fā)現(xiàn)數學的本質屬性和數學知識的邏輯關系.教師可以利用這些矛盾點能讓學生準確把握關鍵，能激活學生的思路;從而融會貫通，打通學生的“任督二脈”.在矛盾形式上聚焦性提高學生數學核心素養(yǎng)，強化培養(yǎng)學生彈性思維高度.

例如：設f(x)為R上的奇函數，且滿足f(x+2)=-f(x)，若f(2)=3，求f(6)的值.

方向1：∵f(x+2)=-f(x)，

∴f(x+2)+f(x)=0 ①，

∴f(x+4)+f(x+2)=0 ②.

②-①得：

∴(x+4)=f(x),∴f(x)的周期T=4，

∴f(6)=f(6-4)=f(2)=3.

方向2：同上可得周期T=4，

∵f(x)為R上的奇函數，

∴f(6)=f(6-8)=f(-2)=-f(2)=-3.

同一個問題，不同方向，等到不同結果，這個矛盾體通過學生的檢驗，不斷深化函數奇偶性與周期的知識，鍛煉辯證思維.彈性思維得到發(fā)展.