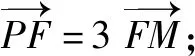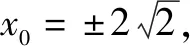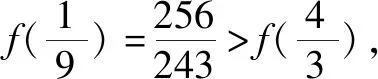解析幾何中的數學思想賞析
黃光鑫 謝 超
(1.四川省成都市四川師范大學附屬中學 610066;2.四川省成都市第二十中學校 610036)
數學思想是對數學事實與理論經過概括后產生的本質認識;基本數學思想則是體現或應該體現于基礎數學中的具有奠基性、總結性和最廣泛的數學思想,它們含有傳統數學思想的精華和現代數學思想的基本特征,并且是歷史地發展著的.
解析幾何的創立在數學的發展史上具有里程碑的意義.學習解析幾何不僅要學習各種不同題型的解答方法,更要透過靈活多樣的方法,領悟其中蘊含的數學思想.
一、函數與方程的思想
函數思想就是利用運動變化的觀點分析和研究具體問題中的數量關系,通過函數的形式把這種數量關系表示出來并加以研究,從而使問題獲解.方程思想是從問題的數量關系入手,運用數學語言將問題中的條件轉化為方程問題,然后通過解方程(組)使問題獲解.函數與方程的思想既是函數思想與方程思想的體現,也是兩種思想綜合運用的體現,是研究變量與函數、相等與不等過程中的基本數學思想.
例1 已知拋物線C:x2=py(p>0)上點M處的切線方程為x+y+1=0.(1)求拋物線C的方程;(2)設A(x1,y1)和B(x2,y2)為拋物線C上的兩個動點,其中y1≠y2,且y1+y2=2,線段AB的垂直平分線與y軸交于點T,求△ABT面積的最大值.
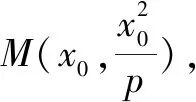
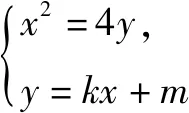
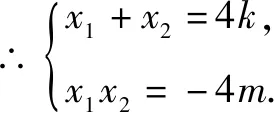
由Δ=16k2+16m>0得:k2+m>0.②
y1+y2=k(x1+x2)+2m=4k2+2m=2?4k2=2-2m.③
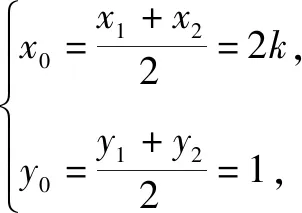
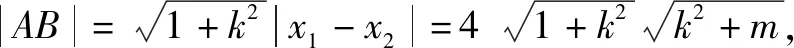

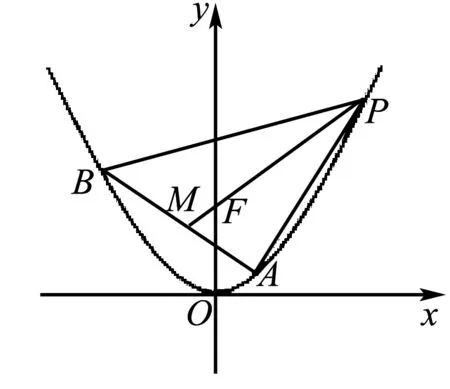
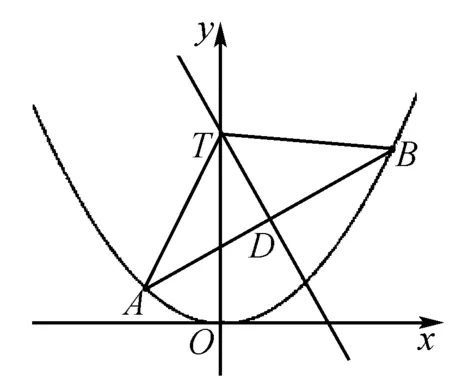
由4k2=2-2m>0得:m<1,將③代入②得:m>-1,∴-1 將③代入④得: 賞析本題將△ABT的面積表示為一個變量m的函數,隨后就可以采用處理一般函數最值的常用辦法(求導)去解決三角形面積的最大值問題. 整理得:2tx1-2y1+1=0.① 設B(x2,y2),同理可得2tx2-2y2+1=0. ② 于是x1+x2=2t,x1x2=-1,y1+y2=t(x1+x2)+1=2t2+1. 賞析本題第(1)問用變量的觀點根據①式、②式以及方程的定義直接得出直線方程的方法值得借鑒!此題是利用變量的觀點將兩個變量統一到一個方程之中.變量是函數的基礎,對應是函數的本質! (2)設兩切線為l1,l2, ①當l1⊥x軸或l1∥x軸時,對應l2∥x軸或l2⊥x軸,可知P(±3,±2); ∴36k2-4[(y0-kx0)2-4]=0, 數形結合的思想就是充分運用“數”的嚴謹和”形”的直觀,將抽象的數學語言與直觀的圖形語言結合起來,使抽象思維和形象思維結合,通過圖形的描述、代數的論證來研究和解決數學問題的一種數學思想方法.數形結合思想是數學的規律性與靈活性的有機結合,通過“以形助數,以數輔形”,變抽象思維為形象思維,使復雜問題簡單化,抽象問題具體化,有助于把握數學問題的本質,有利于達到優化解題的目的. (1)求橢圓C1的方程; 解法2 延長AD、BC交于點F,顯然O為線段AB的中點,又因為OC∥AD,所以點C為線段BF的中點.因為AC是△ABF的中線,DE∥FB,從而點P為線段DE的中點.即|PD|=|PE|. 賞析解析幾何本來就是數形結合的光輝典范!老一輩數學家華羅庚也曾經強調:“數形結合百般好,隔離分家萬事休!”本題解法二充分挖掘圖形的幾何屬性,數形結合,尋找數學美,巧添輔助線,如此機智的證明方法簡直令人拍案叫絕! 分類與整合就是當問題所給的對象不能進行統一研究時,就需要對研究對象按某個標準分類,然后對每一類分別研究得出每一類的結論,最后綜合各類結果得到整個問題的解答.分類與整合就是“化整為零,各個擊破,再積零為整”的數學思想. 解(1)設橢圓長半軸長及半焦距分別為a,c,由已知得 當λ≥1時,點M的軌跡為中心在原點、長軸在x軸上的橢圓. 賞析本題第(2)問由于方程中參數取值的不確定性,因此需要進行詳細的分類討論.分類討論實質上是把一個復雜的數學問題劃分為若干個簡單的數學問題各個擊破!體現出化難為易,化繁為簡的數學思維.分類討論必需做到不重不漏! 化歸與轉化的思想是在研究和解決數學問題時采用某種方式,借助某些數學知識,將問題進行等價轉化,使抽象問題具體化,復雜問題簡單化,未知問題己知化等,進而達到解決問題的數學思想. (1)若|PF|=3,求點M的坐標; (2)求△ABP面積的最大值. “欲窮千里目,更上一層樓!”數學思想是數學的靈魂,只有對數學思想的透徹理解,深刻領悟,才能居高臨下地看待問題,也才能找到更多、更好、更新的解法.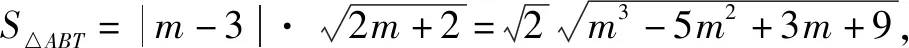
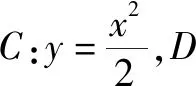
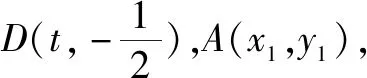
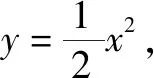




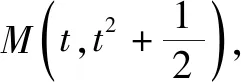


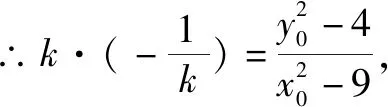

二、數形結合的思想
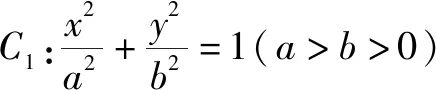
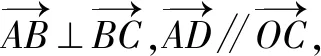

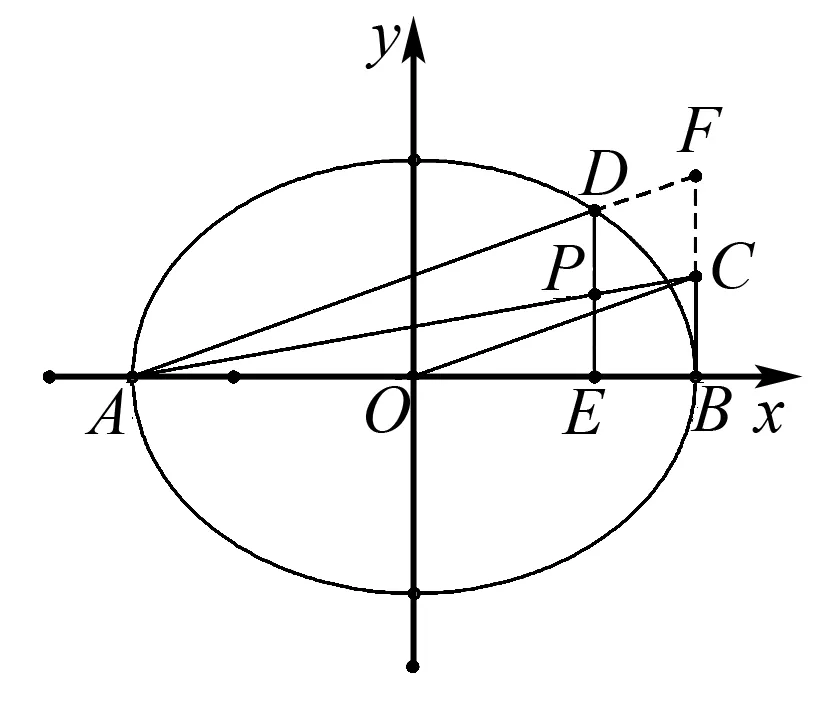
三、分類與整合的思想
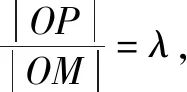
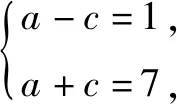

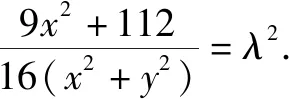

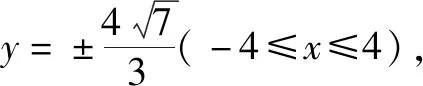
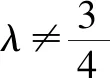
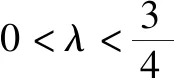
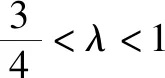
四、轉化與化歸的思想