多通道轉杯紡羊毛混色織物的Friele模型

楊瑞華， 王卓， 鄧茜茜， 徐亞亞

(江南大學 生態紡織教育部重點實驗室，江蘇 無錫 214122)

為滿足市場發展需求，現代紡織技術不斷革新，大量新型紡紗技術應運而生，紗線形式呈現出多樣化趨勢。在各種新型紗線中，色紡紗線因其獨特的外觀、豐富的色彩，加之其生產方法，符合人們追求環保、個性時尚的消費理念，深受消費者青睞[1-2]。傳統混色紡紗的生產是先在前紡工序對有色纖維進行均勻混合，然后再紡制成紗；三通道轉杯紡紗技術是將轉杯紡與復合紡紗相結合，把不同顏色的粗紗條同時喂入轉杯紡紗系統，并均勻混合，一步成紗，不僅縮短了色紗生產流程，還可小批量、多品種生產，快速應對市場需求[3]。轉杯紡作為一種新的紡紗方式，因其流程短、產量高、纖維適應性廣，可循環利用廢棄的羊毛制品或下腳料，在毛紡領域具有很好的發展前景[4-5]。為將三通道轉杯紡紗技術引入毛色紡產品的生產，文中以有色毛纖維為原料，利用三通道轉杯紡紗機生產羊毛混色紗線，并研究混色織物的混色規律，為未來三通道轉杯毛紡產品在計算機測配色方向的發展提供理論依據。

計算機測配色技術以配色模型理論為依據，對來樣進行輔助配色，從而解決工廠配色難、效率低等困難。目前，常用的纖維混色配色模型主要有Kubelka-Munk雙常數模型[6-7]、Stearns-Noechel模型[8-9]以及Friele模型[10-11]，其中Friele模型是唯一在光學理論基礎上針對色纖維混合特征而提出的配色模型。文中利用Friele模型分別對三通道轉杯羊毛混色針織物及梭織物的混色規律進行探究，并分析Friele模型是否適用于三通道轉杯毛紡混色織物的測配色。

1 材料與方法

1.1 原料與儀器

1.1.1原料 紅、黃、藍純色羊毛粗紗，浙江蘭寶毛紡集團有限公司生產。

1.1.2儀器 Datacolor 650分光光度儀，美國 Data-color公司制造。

1.2 實驗方法

1.2.1紡紗方法 利用多通道轉杯紡紗機混與紡一體式的獨特紡紗方法，將紅、黃、藍3色羊毛粗紗同時喂入由獨立伺服電機控制的給棉羅拉中，通過給棉羅拉的給棉速度控制纖維混色比例，并在轉杯紡紗機獨有的分梳輥及轉杯裝置的高速運轉下，將喂入的不同顏色的粗紗條進行分梳及均勻混合，紡制出一定比例混合均勻的混色紗線[12]。

1.2.2樣品制備 紡制了紅、黃、藍3種純色紗，并以質量比為10%的變化梯度將3種顏色兩兩混合紡制混色紗，共30個紗樣，分別織成緯編針織平紋織物和梭織斜紋織物，用于求解不同織物結構下的最佳參數σ值。其中紗線線密度為44.85 tex，緯編針織平紋織物的線圈密度為108 個/cm2，梭織斜紋織物的經密為306 根/dm、緯密為192 根/dm。利用紅、黃兩色纖維混合制成的不同比例混色針織物及梭織物分別如圖1和圖2所示。由圖1和圖2可以看出，利用相同紗線不同織造形式織出的織物在顏色及視覺效果上稍有不同，針織物有較明顯的色斑效果，而梭織物由于經緯紗交織，弱化了色斑，在縱向上呈條紋效應。

圖1 不同混色比例針織物Fig.1 Knitted fabrics of different color blending ratios

圖2 不同混色比例梭織物Fig.2 Woven fabrics of different color blending ratios

1.2.3測試方法 織物樣本采用分光光度儀測量其各波長下的光譜反射率。測量環境為：D65標準光源，10°視場，30 mm大孔徑。為減少測量誤差，測量時保證樣本不透光，每個樣本測量10次，取其平均值，波長取值范圍為380～700 nm，取點間隔為10 nm，即每個樣本共有33個波長下的光譜反射率值。

2 Friele模型及參數σ計算

當不同顏色的單色纖維根據不同質量比進行混合時，其形成的混色樣品反射率與單色纖維的反射率假設存在以下加和關系：

f[Rb(λ)]=∑xif[Ri(λ)]

(1)

式中：Rb(λ)表示波長為λ時混色樣品反射率；xi為混色樣品中第i組分單色纖維的質量分數，且滿足∑xi=1；Ri(λ)表示第i組分單色樣品在波長為λ時反射率。

1952年，Friele在加和公式的基礎上推出了一個關于反射率的函數式，即Friele模型，具體表示為

f[R(λ)]=e-σ[1-R(λ)]2/2R(λ)

(2)

式中：R(λ)表示波長為λ時的反射率；σ為Friele模型參數。

Friele模型可用于有色纖維的混色研究。 Friele利用松散的羊毛纖維進行混色，推薦模型參數σ值為0.3。由于σ的取值受到纖維種類、混合方式等諸多方面因素的影響，于是許多研究者對σ的取值展開了進一步探討。PHILIPS等[13]對棉混色紗條的推薦σ值為0.245；沈加加等[14]對條子混色的棉和羊毛混色紗線的推薦σ值分別為0.128，0.093。

由式(2)即可反推出預測樣本的反射率

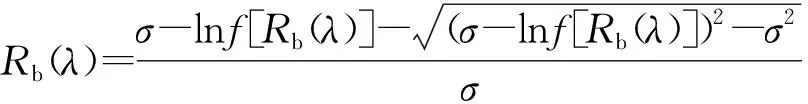
文中通過多通道轉杯紡紗機對有色纖維進行混色，并利用賦值法對Friele模型參數σ進行循環賦值(賦值范圍為0.001～1，賦值間隔為0.001)，分別求取針織樣品和梭織樣品平均色差最小時σ的取值作為最佳σ值，從而利用最優參數建立關于多通道轉杯毛紡混色織物的Friele模型。文中色差計算均采用CMC(2∶1)色差公式。不同賦值參數下樣品平均色差的取值變化如圖3所示。

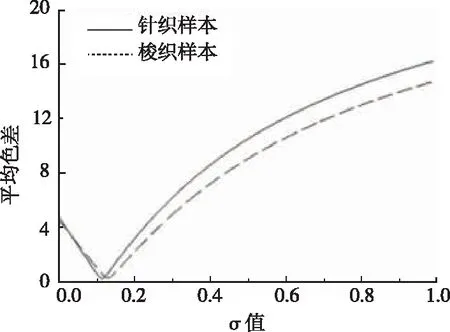
圖3 不同σ值對應織物樣品平均色差Fig.3 Average color differences of fabric samples with different σ values

由圖3可以看出，針織樣品和梭織樣品的平均色差隨著σ值的增大，呈先減小后逐漸增大的趨勢；當σ值在0.1～0.2范圍內時，樣品平均色差達到最小。為清楚地呈現出樣本平均色差在0.1～0.2范圍內的變化情況，在0.1～0.2區間內作平均色差變化圖，具體如圖4所示。由圖4可以看出，兩種織物樣品的平均色差在此范圍內因σ值的不同變化差異較大。當σ值為0.125時，針織樣品的平均色差達到最小；當σ值為0.141時，梭織樣品的平均色差達到最小。因此取針織物的Friele模型最優σ值為0.125，梭織物的Friele模型最優σ值為0.141。

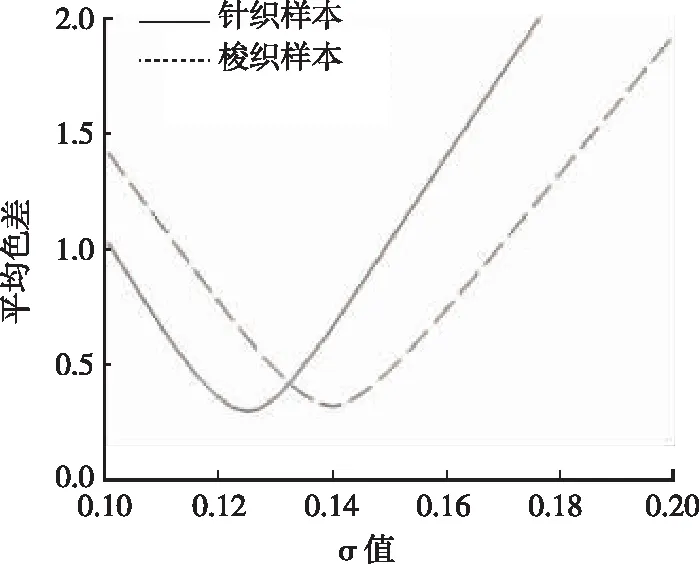
圖4 σ值在0.1～0.2區間內的織物平均色差Fig.4 Average color differences with the value of σ in the range of 0.1～0.2

3 配方計算

根據求得的最優模型參數，利用全光譜配色法對樣本進行配方預測，假設在預測配方下標準樣反射率與配色樣反射率無限接近，即滿足[15]

Rs(λ) ≈Rm(λ)

(4)

式中：Rs(λ)為各波長下標準樣反射率，Rm(λ)為各波長下配色樣反射率。

由式 (2)可推得

f[Rs(λ)] ≈f[Rm(λ)]

(5)

對于3組分樣品配色，由式(1)可得到

f[Rm(λ)]=x1f[R1(λ)]+x2f[R2(λ)]+x3f[R3(λ)]

(6)

設

可得到Fs≈FX

(7)

利用式(7)中的33個線性方程組求解3個未知數，則方程有解，且為多個解，因此利用最小二乘法求方程組的解，即使Δ→0

x2f[R2(λ)]-x3f[R3(λ)]}

解得>X=(FTF)-1FTFs

(8)

利用最小二乘法求解出的預測配方使得匹配樣與標準樣之間反射率差異最小，但為保證各單色纖維預測配方和為1，需對以上求得的配方進行歸一化處理，作為最終的預測配方。

4 預測結果分析

根據求得的預測配方，即可預測混色樣關于Friele模型的f[Rb(λ)]，并利用式(3)可以計算出預測混色樣的反射率Rb(λ)，根據標準混色樣與預測混色樣的反射率，計算預測配方下預測樣品的色差。

為驗證預測配方的準確性，文中在針織樣品和梭織樣品中分別選取10種不同比例的3色混色樣品，利用最優模型參數即式(8)，對樣品進行配方預測及預測配方下樣品色差計算，其中1～10號驗證樣品為緯編針織平紋織物，11～20號驗證樣品為梭織斜紋織物。各樣品配色結果見表1和表2。

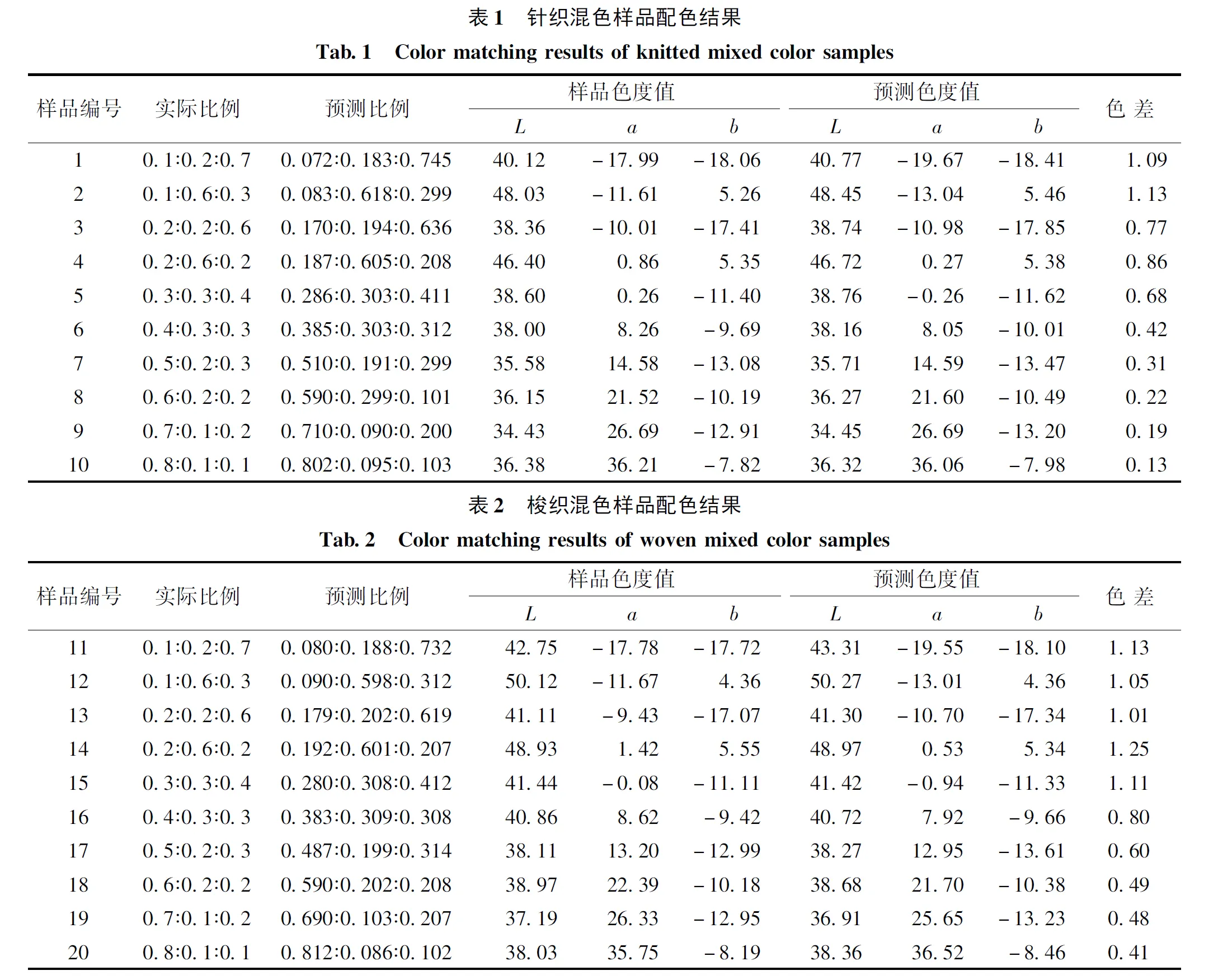
由表1可知：當σ1=0.125，對針織樣本進行配方預測時，有兩個樣品色差大于1，其他均小于1，平均色差為0.58；當σ2=0.141，對梭織物進行配方預測時，其驗證樣品的色差在1左右，平均色差為0.83。兩種織物的平均色差均小于1，且每個樣品的色差均在1個色差單位左右，有效滿足了行業內人眼識別的色差要求，預測效果相對較好，說明Friele理論能夠較好地應用于多通道轉杯毛紡混色織物的纖維混色配比及顏色預測的研究。

5 結語

文中將Friele模型應用于三通道轉杯羊毛混色織物的混色規律研究，利用賦值迭代法計算出適用于緯編針織平紋織物的模型參數σ為0.125，適用于梭織斜紋織物的模型參數σ為0.141。將求出的模型參數進行配色，并計算色差，結果顯示：樣品色差均在1左右，平均色差小于1，滿足配色要求，預測效果相對較好。

多通道轉杯紡紗技術能夠將混色與紡紗一體化生產，在未來色紡領域具有較好的發展前景。計算機測配色技術是未來色紡紗發展的必然趨勢，將多通道轉杯紡紗技術與配色計算技術相結合，可為未來多通道轉杯紡純羊毛混色織物計算機配色軟件的開發及應用提供一定的理論依據。