采氣速度對氣田產量峰值預測模型的影響分析

方一竹 ，余 果，李海濤，徐 凌，陳艷茹，付 玉，王 升

（1.中國石油西南油氣田勘探開發研究院，四川成都 610041；2.西南石油大學，四川成都 610500）

在氣田開發的實際工作中，對產量、累積產量和可采儲量的正確預測，始終是油氣藏工程師的重要任務。油氣田開發指標預測的準確性和可靠性，會影響到編制中長期開發規劃的效果，對于指導氣田方案編制具有重要的參考意義[1]。從預測方法的本身來說，模型預測法具有較為普遍的適用性，不受氣田開發階段和氣田類型的影響，已在天然氣產量預測領域得到廣泛應用[2-5]。我國著名地球物理學家翁文波于1984 年在專著《預測論基礎》中提出泊松旋回模型（又稱翁氏模型）[6]，為我國油氣田產量預測奠定了幾種油氣田產量預測模型的對比基礎[7]。之后，其他學者相繼提出了多種預測模型[8]，包括廣義翁氏模型、HCZ 模型[9]、瑞利（Rayleigh）模型[10]、威布爾（Weibull）模型[11]、哈伯特模型[12]、胡張陳模型[13]、對數正態分布模型[14]等預測模型。本文主要研究了采氣速度與4 個模型參數的影響因素，利用預測模型建立起采氣速度和產量曲線特征之間的聯系。

1 建立油藏數值模擬模型

為研究模型的影響因素，需建立油藏數值模擬模型。從文獻可以看出，影響氣藏產量的因素主要有：滲透率、采氣速度、地層壓力、有效厚度、井控半徑等，對于已經投入生產的氣藏，采氣速度具有較高的研究價值。本文利用數值模擬方法建立典型氣藏模型，開展采氣速度影響研究。機理模型基本參數（見表1、圖1）。

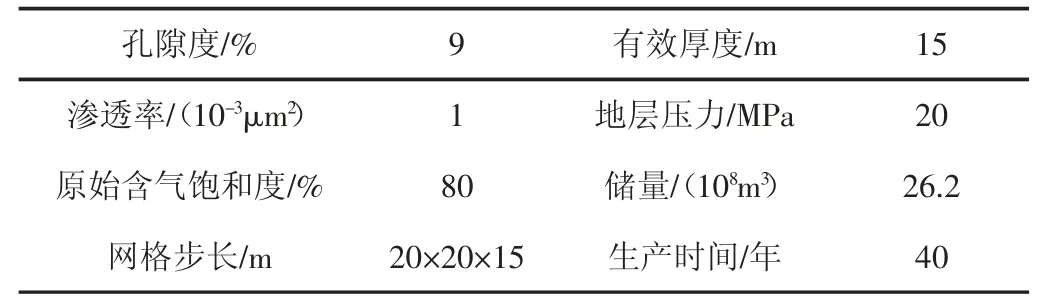
表1 氣藏機理模型參數表

表2 氣藏采氣速度設計表

按照設計好的模型參數（見表2）建立模型后進行全生命周期的生產模擬，分別得到不同的年產量數據。利用各個模型，結合數值模擬數據進行產量和累積產量的預測，使用MATLAB 軟件編程，得到預測公式和預測圖形。部分實驗數據的預測曲線圖（見圖2、圖3）。

圖1 氣藏機理模型

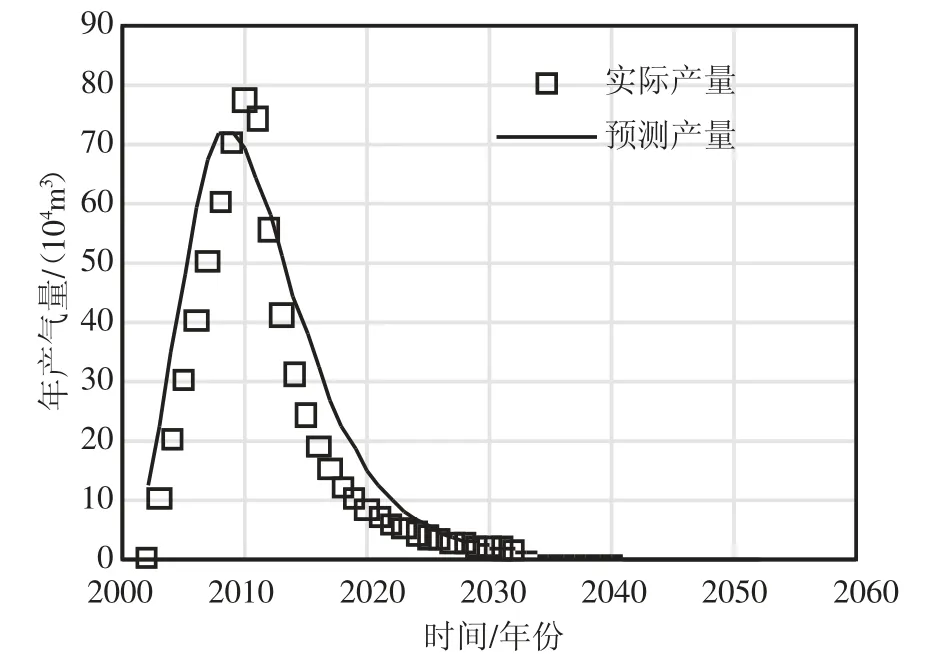
圖2 HCZ 模型年產量擬合

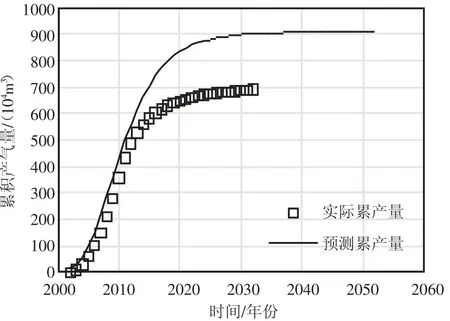
圖3 HCZ 模型累積產量擬合

2 采氣速度影響分析

2.1 HCZ模型

1995 年，胡建國、陳元千、張盛宗提出了HCZ 模型預測油氣田產量和累積產量。HCZ 模型預測產量和累積產量的表達式為：

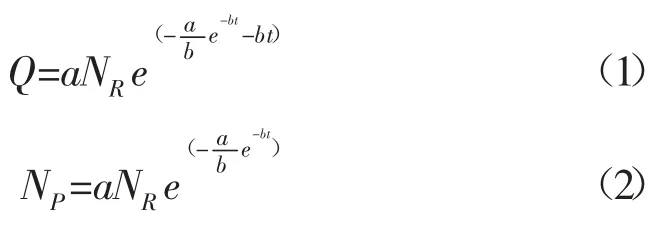
模型的半對數線性表達式為：

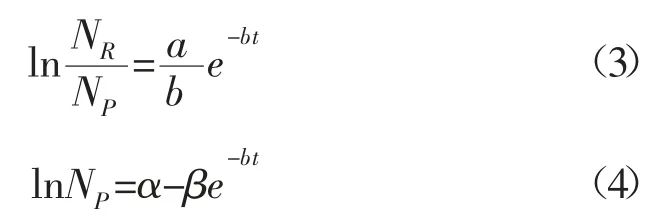
根據氣田的實際生產數據，可由式（3）和式（4）分別線性回歸求得截距和斜率，進而求得模型的預測公式中參數a，b 和NR的值，即可得到氣田的HCZ 模型的具體預測公式。HCZ 模型的產量計算公式（1）是年產量Q 關于時間t 的函數，影響曲線形態的參數共有a，b和NR。分別改變三個參數的大小，繪制出對應的年產量曲線（見圖4）。

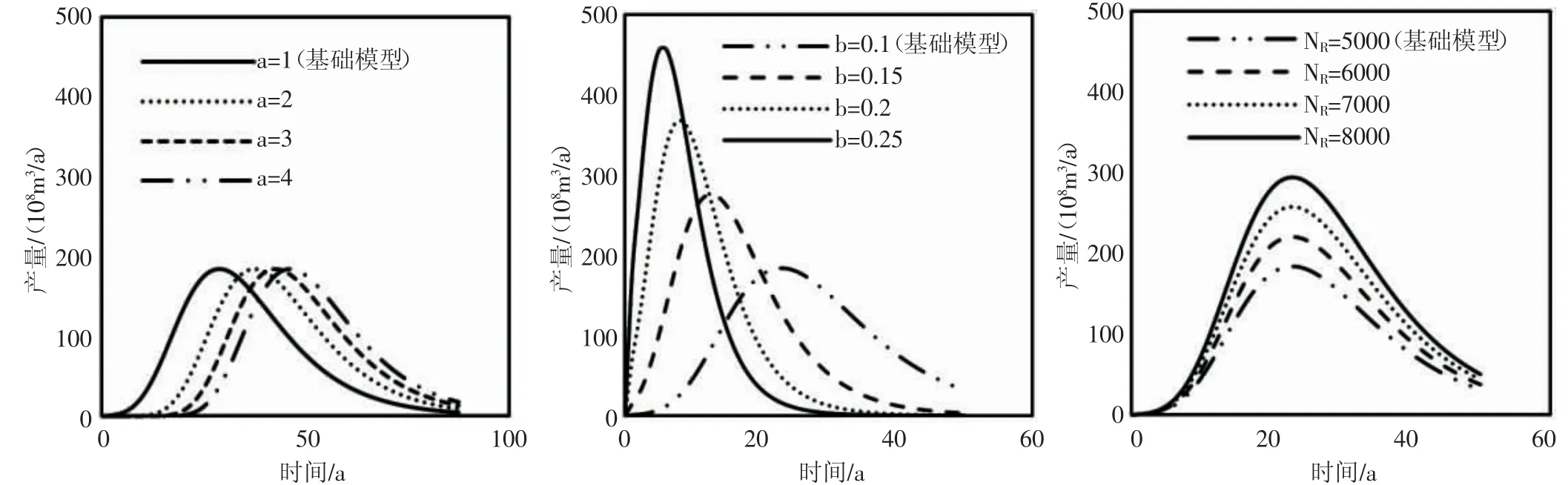
圖4 參數對HCZ 模型曲線形態影響

參數a 增大使峰值產量發生時間滯后，表現為圖形峰值右移；對可采儲量沒有影響。參數b 增大使得峰值產量增大，峰值時間提前，表現為圖形峰值左移和上移；對可采儲量沒有影響。參數NR增大使峰值產量增大，峰值時間不變，表現為圖形峰值上移；使可采儲量增大。

在不同采氣速度下，對得到的年產量數據模擬，分別得到對應的HCZ 模型預測公式。根據采氣速度和模型參數分析結果可知，在實驗因素變化范圍內（見圖5）。

參數a 與采氣速度反相關。結合圖4 可知，當采氣速度增大時，產量的峰值發生時間提前，上產與遞減均變快；峰值大小不變化。參數b 與采氣速度三次方正相關。結合圖4 可知，當采氣速度增大時，產量的峰值發生時間提前，上產與遞減均變快，峰值升高。參數NR與采氣速度正相關，具有較高的線性相關性。結合圖4 可知，當采氣速度增大時，產量的峰值升高。

2.2 瑞利模型

瑞利模型由陳元千等建立，可用于預測油氣田的產量、累積產量、可采儲量、最高年產量及其相應的開發時間和累積產量。應用實例證明該模型有廣泛的有效性。瑞利模型預測產量和累積產量的表達式為：

圖5 采氣速度對HCZ 模型參數的影響

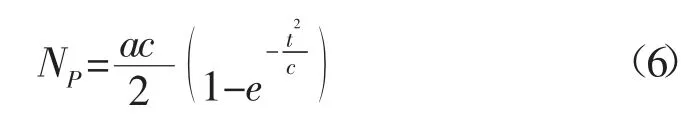
利用瑞利模型進行各項預測必須先確定模型常數a 和c。為此，將式（5）兩端先除以t 再取常用對數，得：

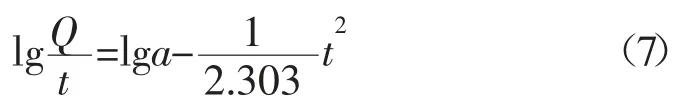
可改寫為如下形式：

根據氣田的實際生產數據，由式（8）進行線性回歸后，求得直線截距α 和斜率β 即可確定常數a 和c 的數值。瑞利模型的產量計算公式（5）是年產量Q 關于時間t 的函數，影響曲線形態的參數有a 和c。分別改變兩個參數的大小，繪制出對應的年產量曲線（見圖6）。

參數a 增大使產量峰值升高，峰值發生時間不變；使可采儲量增大。參數c 增大使得產量的峰值增大，峰值發生時間提前，表現為圖形峰值左移和上移；使可采儲量增大。

在不同的采氣速度下，對得到的年產量數據模擬，分別得到對應的瑞利模型預測公式。根據采氣速度和模型參數分析結果可知，在實驗因素變化范圍內（見圖7）。

參數a 與采氣速度的平方正相關。結合圖6 可知，當采氣速度增大時，產量的峰值升高，峰值發生時間不變。參數c 與采氣速度的平方反相關。結合圖6 可知，當采氣速度增大時，采氣速度增大使峰值降低，峰值發生時間提前。

2.3 對數正態分布模型

對數正態分布模型是基于對概率統計學中對數正態分布建立的預測油氣田產量、可采儲量、最大年產量及其發生時間的數學模型。對數正態分布的數學模型為：

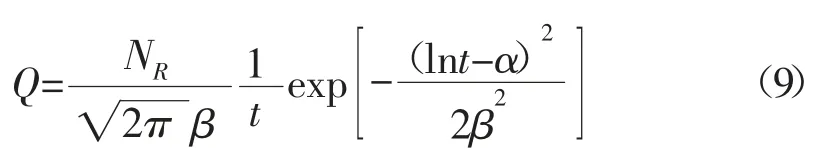
對式（9）等號兩端取常用對數得：

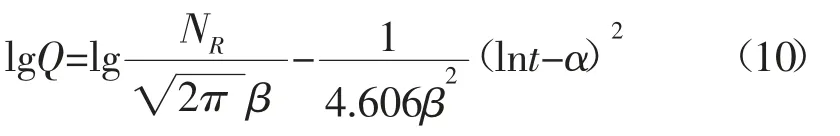
若給定不同的α，利用式（10）進行線性試差求解，對于能夠得到最大相關系數的直線的α 值，即為要求的正確的值。再通過線性回歸，可以分別得到可采儲量NR和參數β 的數值。對數正態分布模型的產量計算公式（9）是年產量Q 關于時間t 的函數，影響曲線形態的參數有α、β 和NR。分別改變三個參數的大小，繪制出對應的年產量曲線（見圖8）。

參數α 增大使峰值產量降低，峰值發生時間滯后，表現為圖形峰值向右下方移動。參數β 增大使得峰值產量增大，峰值發生時間提前。參數NR增大使峰值產量增大，峰值發生時間不變，表現為圖形峰值上移。

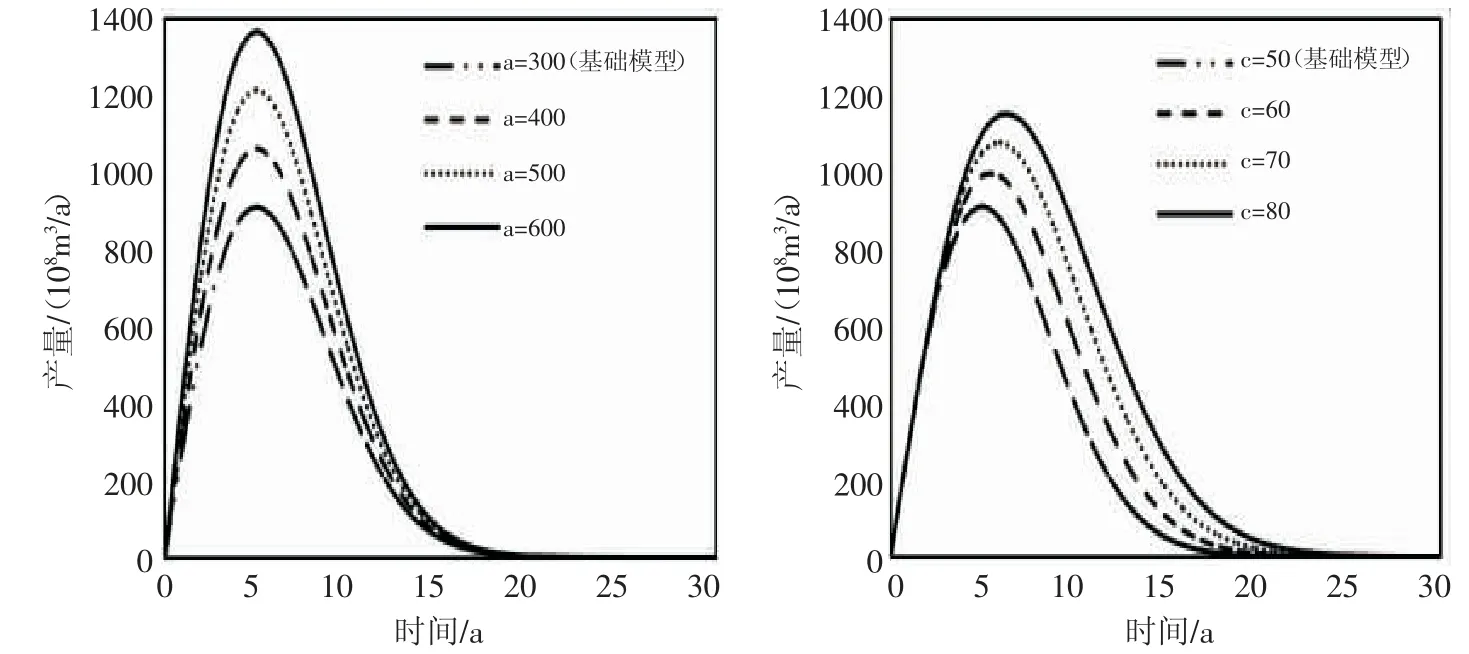
圖6 參數對瑞利模型曲線形態影響

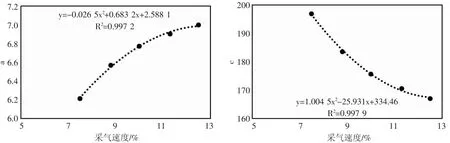
圖7 采氣速度對瑞利模型參數的影響

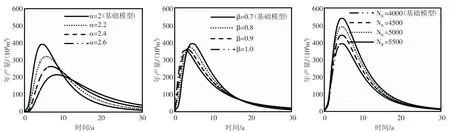
圖8 參數對對數正態分布模型曲線形態影響

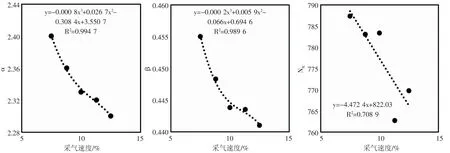
圖9 采氣速度對對數正態分布模型參數的影響

在不同的采氣速度下，對得到的年產量數據模擬，分別得到對應的對數正態分布模型預測公式。根據采氣速度和模型參數分析結果可知，在實驗因素變化范圍內（見圖9）。

參數α 與采氣速度的三次方反相關。結合圖8 可知，當采氣速度增大時，年產量的峰值升高，峰值發生時間提前。參數β 與采氣速度的三次方反相關。結合圖8 可知，當采氣速度增大時，年產量的峰值升高，峰值發生時間提前。參數NR與采氣速度之間沒有明顯的相關性。

2.4 胡張陳模型

胡張陳模型是基于對大量油氣田開發實際動態資料的統計研究，建立的一種預測油氣田產量、累積產量、可采儲量、最高年產氣量及其發生的時間的模型。該模型不僅適用于油氣田產量存在單峰的情形,而且也適用于油氣田投產之后持續遞減的情形。胡張陳模型的數學模型為：

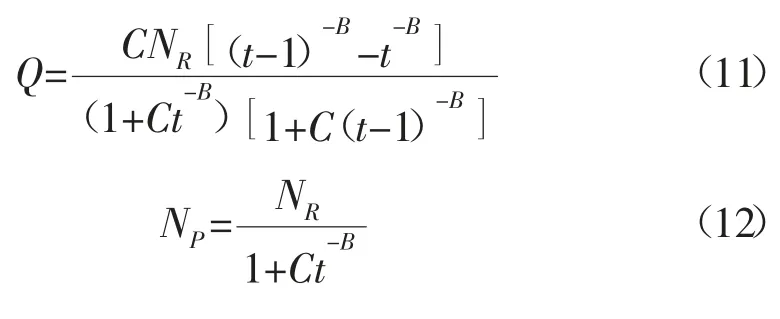
對式（11）和式（12）處理可得：

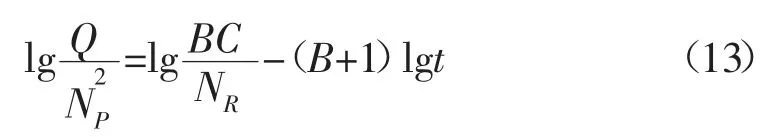
對氣田的年產量與累積產量平方之比與生產時間之間的雙對數進行線性回歸，即可得到模型參數。胡張陳模型的產量計算公式（11）是年產量Q 關于時間t 的函數，影響曲線形態的參數有B、C 和NR。分別改變三個參數的大小，繪制出對應的年產量曲線（見圖10）。

參數B 增大使峰值產量升高，峰值發生時間提前，表現為圖形峰值向左上方移動。參數C 增大使得峰值產量稍微降低，峰值發生時間滯后。參數NR增大使峰值產量增大，峰值發生時間不變，表現為圖形峰值上移。

在不同的采氣速度下，對得到的年產量數據模擬，分別得到對應的胡張陳模型預測公式。根據采氣速度和模型參數分析結果可知，在實驗因素變化范圍內（見圖11）。

參數B 與采氣速度的三次方正相關。結合圖10 可知，當采氣速度增大時，年產量的峰值升高，峰值發生時間提前。參數C 與采氣速度反相關。結合圖10 可知，當采氣速度增大時，年產量的峰值升高，峰值發生時間提前。參數NR與采氣速度正相關。結合圖10 可知，當采氣速度增大時，年產量的峰值升高，峰值發生時間不變。

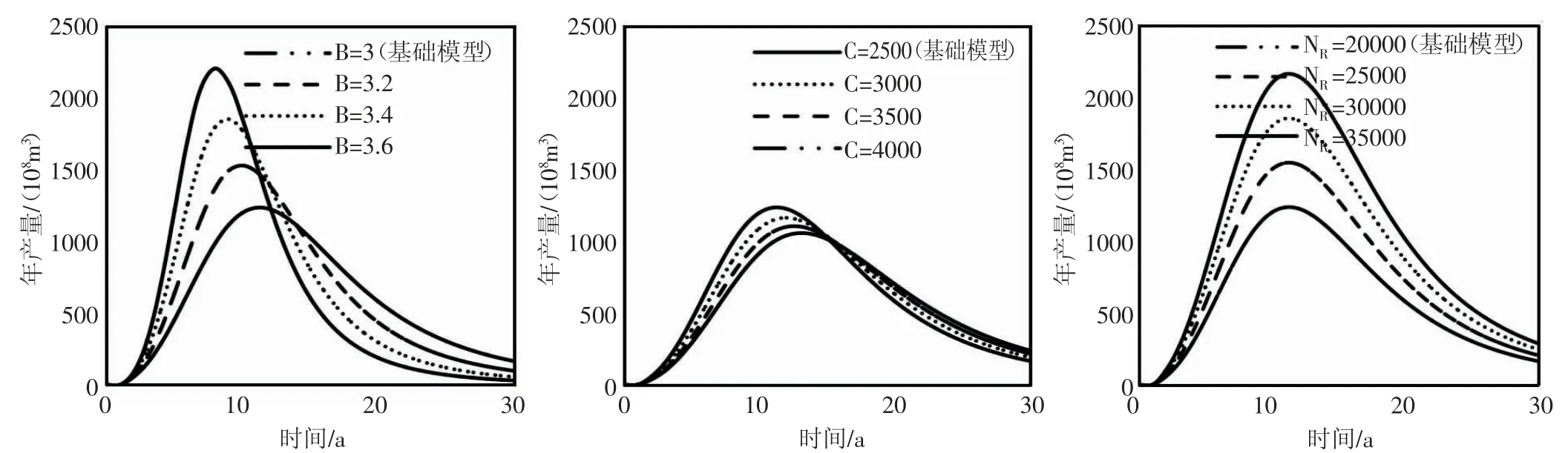
圖10 參數對胡張陳模型曲線形態的影響

圖11 采氣速度對胡張陳模型參數的影響

3 結論

（1）使用HCZ 模型、瑞利模型、對數正態分布模型和胡張陳模型對氣藏產量進行預測時，氣藏采氣速度的變化會體現在預測模型的參數變化中。

（2）氣藏采氣速度的變化，與預測模型的參數之間具有緊密的數學聯系。因此在氣田開發過程中，可提前預測采氣速度改變對氣田峰值的影響。