巧構輔助圓 妙解幾何問題
鄭惠容
(福建省泉州市石獅市華僑中學 362700)
圓的有關知識是每年中考必考的內容之一.縱觀近幾年福建省的中考或質檢的數學試題會發現,最后的兩道壓軸題中有時沒有明顯的圓的身影存在.但如果我們認真審題,就會發現,其實根據題目中的條件,我們可以自己構造一個輔助圓.那么怎樣構造輔助圓呢?筆者結合實例,談談構造輔助圓的基本做法.
一、立足基礎,利用圓的定義構造輔助圓
根據圓的定義:到一個定點的距離等于定值的點在同一個圓上.這是利用圓的定義添輔助圓的最基本方法.
例1(2016-2017學年福州市期末試題)如圖1,C為線段AB上一點,分別以AC,BC為邊在AB的同側作等邊三角形△HAC與等邊△DCB,連接DH.

(2)在(1)的條件下,作點C關于直線DH的對稱點E,連接AE,BE,求證:CE平分∠AEB;

(3)現將圖1中△DCB繞點C順時針旋轉一定角度α(0°<α<90°),如圖2,C關于直線DH的對稱點為E,則(2)中的結論是否成立并證明.
分析(3)根據對稱性可知:HE=HC,又因為AH=HC,從而有HC=HA=HE,即A、C、E三點共圓.同理可知B、C、E三點也共圓.
證明(1)(2)略.

(3)結論仍正確.理由如下:
如圖3,由對稱性可知:HC=HE.
又∵HA=HC,∴HC=HA=HE,
∴A、C、E三點都在以點H為圓心,HA為半徑的圓上.

∴∠AEC=∠BEC,∴EC平分∠AEB.
本題解題的關鍵在于能夠根據圓的定義,發現A、C、E三點在以點H為圓心的圓上,同樣B、C、E三點在以點D為圓心的圓上,這樣做出輔助圓后,就可利用圓周角定理解決問題了.
二、能力導向,利用90°的圓周角所對的弦是直徑得到輔助圓
如果題目中出現三角形有一內角為90°,有時可以利用90°的圓周角所對的弦是直徑得到輔助圓,然后把問題轉化為圓中的問題,利用與圓有關知識來解決相關的問題,這體現了能力導向下培養學生數學思維.
例2(2013年福建省泉州市質檢試題)如圖4,在Rt△ABC中,∠ACB=90°,AC=10cm,BC=5cm,點P從點C出發沿射線CA以每秒2cm的速度運動,同時點Q從點B出發沿射線BC以每秒1cm的速度運動.設運動時間為t秒.

(1)(2)略.
(3)若∠ACB的平分線CE交△PCQ的外接圓于點E.試探求:在整個運動過程中,PC、QC、EC三者存在的數量關系式,并說明理由.
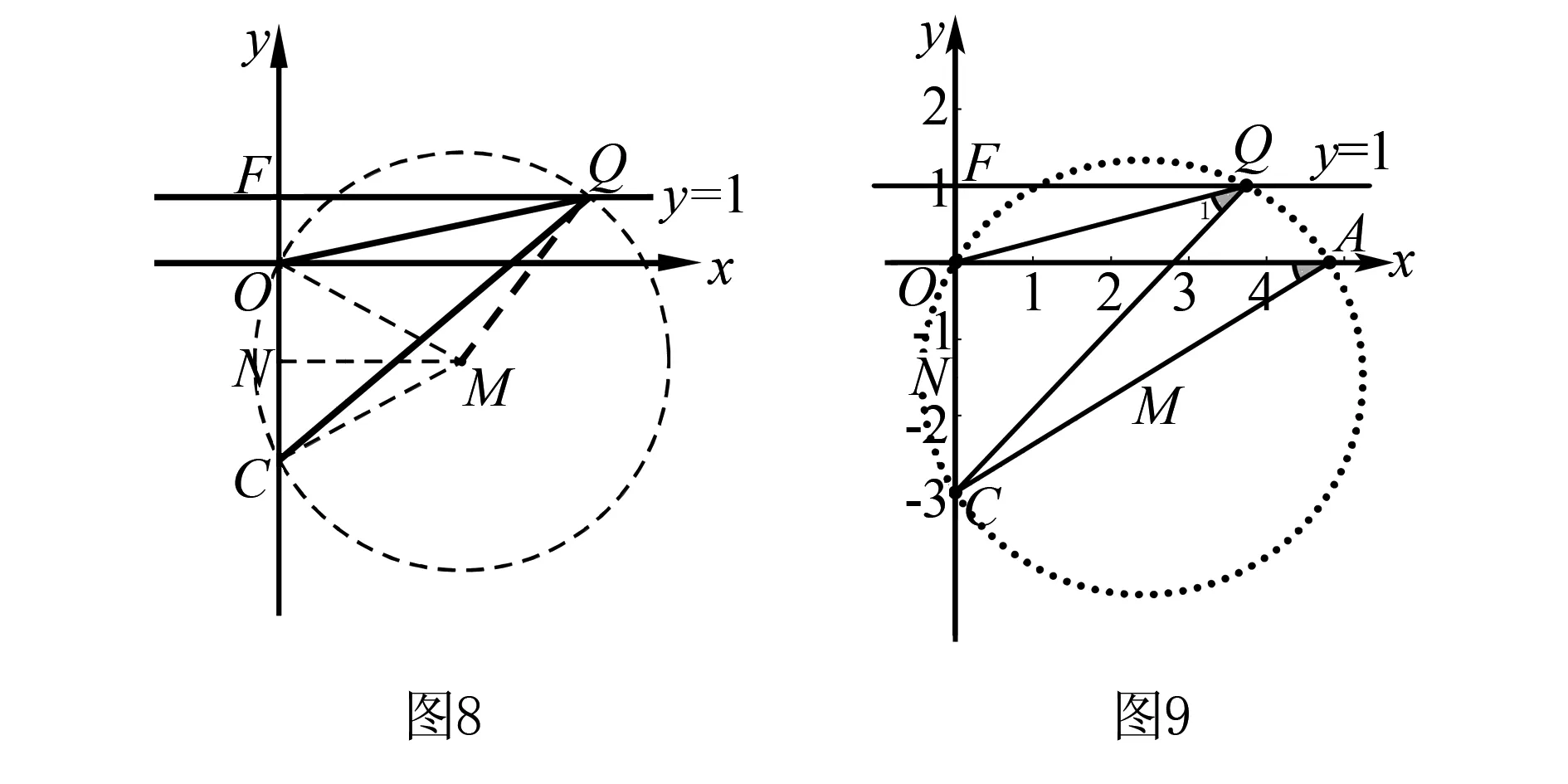
解(3)當0 ∵∠ACB=90°,∴PQ是△CPQ外接圓的直徑, ∴∠QEP=90°即∠QEC+∠PEC=90°. 又∵CE平分∠ACB且∠ACB=90°, ∴∠QCE=∠PHE=45°, ∴△QCE≌△PHE(AAS),∴QC=PH. 在Rt△HEC中,EC2+EH2=HC2,EC=EH, 本題中,題目中并沒有給出圓,這時要根據題目中給出的條件,畫出△CPQ的外接圓,這樣才能結合圓的有關性質、全等三角形和勾股定理來解決問題. 我們知道,不在同一直線的三點確定一個圓,有時可以利用這個基本事實來作輔助圓,特別是當三角形的一邊為定值,而第三個頂點是一個動點時,要求與角有關的問題,可嘗試作出輔助圓,看是否可以把問題轉化為圓的有關計算.這需要更高層次的思維,因此,要關注學生差異,撫平臺階,讓不同學習水平的學生得到不同程度的發展. 例3(2015年福建省泉州市質檢試題)如圖7,O是坐標原點,過點A(-1,0)的拋物線y=x2-bx-3與x軸的另一個交點為B,與y軸交于點C,其頂點為D點. (1)求b的值. (2)連結BD、CD,動點Q的坐標為(m,1). ①當四邊形BQCD是平行四邊形時,求m的值; ②連結OQ、CQ,當∠CQO最大時,求出點Q的坐標. 分析我們發現(2)中②問題中的△CQO的邊OC是個定值,所以可大膽地構造出△CQO的外接圓⊙M,從而把∠CQO轉化為圓心角∠CMO的一半來求. 解(1)(2)①略. ∴sin∠CQO的值隨著OM的增大而減小. 又∵MO=MQ,∴當MQ取最小值時sin∠CQO最大, 即當MQ⊥直線y=1時,∠CQO最大, 此時⊙M與直線y=1相切. ∴Q1(2,1). 根據對稱性,另一點Q2(-2,1)也符合題意. 綜上所述,Q1(2,1),Q2(-2,1). 我們也可以設⊙M與x軸交于點A(如圖9),這樣就可以直接利用同弧所對的圓周角相等,把∠CQO轉化為Rt△OAC中的∠OAC來解決. 本題的成功之處在于構造了過O、C、Q三點的⊙M,從而利用圓周角與圓心角之間的關系或同弧所對的圓周角相等、垂徑定理、銳角三角函數的定義以及直線與圓的位置關系來解決問題. 從上面的幾個例子我們可以發現,有些問題看似與圓無關,但根據問題的題設、結論或是圖形提供的某些與圓的性質相關的信息,可以構造出輔助圓,然后就可以利用圓的相關性質來解決問題.事實告訴我們,只要能掌握好構造圓的基本方法構造出輔助圓,很多看似很難的幾何問題就可以迎刃而解.輔助圓,是解決相關幾何問題的“金鑰匙”.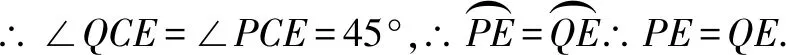




三、關注差異,作三角形的外接圓