小學數(shù)學“問題+圖示”的研課模式探微

劉振雄

【摘要】“問題”的設(shè)計體現(xiàn)了“發(fā)現(xiàn)和提出問題、分析和解決問題”的思考的全過程;“圖示”的設(shè)計呈現(xiàn)能恰如其分地揭示知識的本質(zhì)，一目了然，運用“問題+圖示”研課模式指導(dǎo)小學教師備課和上課，在課堂教學中已經(jīng)取得了比較滿意的效果。

【關(guān)鍵詞】問題;圖示;研課模式

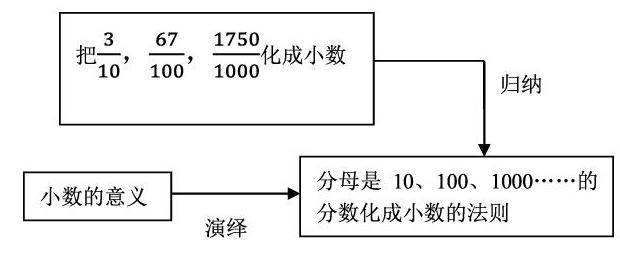
《義務(wù)教育數(shù)學課程標準（2011年版）》指出：教師教學應(yīng)該以學生的認知發(fā)展水平和已有的經(jīng)驗為基礎(chǔ)，面向全體學生，注重啟發(fā)式和因材施教。教師要發(fā)揮主導(dǎo)作用，處理好講授與學生自主學習的關(guān)系，引導(dǎo)學生獨立思考、主動探索、合作交流，使學生理解和掌握基本的數(shù)學知識與技能，體會和運用數(shù)學思想與方法，獲得基本的數(shù)學活動經(jīng)驗。 課本中“問題”的設(shè)計，不僅呈現(xiàn)了利于學生討論的一個個問題，鼓勵學生探索與交流，更重要的是對關(guān)鍵性問題，通過“圖示”形式，給出學生可能出現(xiàn)的思路和想法，為學生的學習和教師的教學提供了方向和腳手架。“問題”的設(shè)計體現(xiàn)了“發(fā)現(xiàn)和提出問題、分析和解決問題”的思考的全過程，既利于學生的學，又利于教師的教。“圖示”的設(shè)計呈現(xiàn)能恰如其分地揭示知識的本質(zhì)，一目了然，“越過”直線形文字語言思維的“障礙”，直接與人腦深層思維“掛鉤”，免去語言，文字在頭腦中“翻譯”、轉(zhuǎn)化程序，便于學生理解，接收信息，從而提高教學效率。下面就結(jié)合學生的認知規(guī)律，對北師大版五年級下冊《“分數(shù)王國”與“小數(shù)王國”》中的“分數(shù)化小數(shù)”作了調(diào)整與組合，運用“問題+圖示”模式對它進行教學設(shè)計。

2.圖示

突破“分數(shù)化小數(shù)”整節(jié)課重難點教與學的圖示：

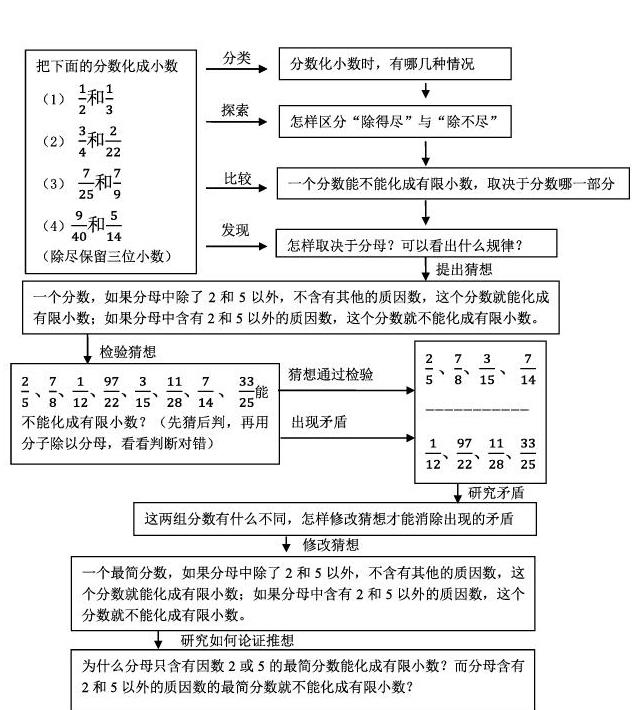
按照這樣的思路，通過上述設(shè)計的系列問題的啟發(fā)和誘導(dǎo)，首先讓學生從具體事例的研究開始，運用觀察、比較、分類、歸納等方法提出猜想，然后檢驗猜想，即運用演繹的方法，根據(jù)猜想做出推論，并且考察推出的判斷是否正確，由于檢驗中出現(xiàn)了矛盾，說明猜想必須修改，科學的結(jié)論必須經(jīng)過證明才能確認。運用“問題”+“圖示”模式研課設(shè)計如下圖：

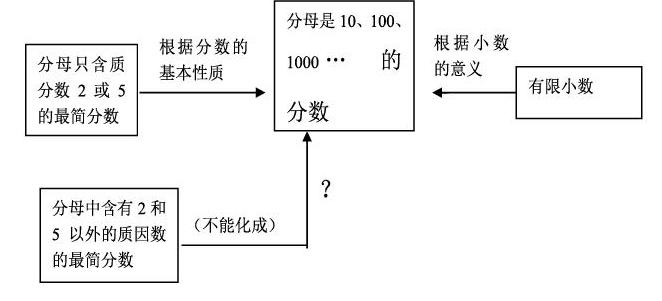
小學數(shù)學活動中的證明必須適應(yīng)小學生的知識基礎(chǔ)和思維能力水平。在這里，我們首先使小學生認識到：根據(jù)小數(shù)的意義，分母是10、100、1000…的分數(shù)和有限小數(shù)可以互化。然后注意，分母只含有質(zhì)因數(shù)2或5的最簡分數(shù)，由于它們總能化為分母是10，100，1000…的分數(shù)，因而都能化為有限小數(shù)。而那些分母含有2和5以外的質(zhì)因數(shù)的最簡分數(shù)，由于不能化成分母是10，100，1000…的分數(shù)，因而不能化為有限小數(shù)，由于上述論證猜想的過程，是結(jié)合具體事例并在教師幫助下逐步進行的，所以小學生對此不會感受到太大的困難。按照這樣的“問題+圖示”模式指導(dǎo)小學教師備課和上課，在實際教學中已經(jīng)取得了比較滿意的效果。

參考文獻：

[1]中華人民共和國教育部.義務(wù)教育數(shù)學課程標準（2011版）[S].北京：北京師范大學出版社，2012：1.