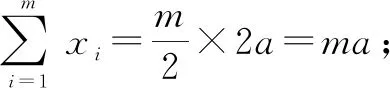函數對稱性的“新面孔”
2020-03-30 05:35:28梁宗明
數理化解題研究 2020年7期
梁宗明
(甘肅省蘭州市蘭化一中 730060)
高中數學教學中經常出現一種題型,求兩個函數圖象所有交點的橫坐標之和是多少.此類問題中具體交點的橫坐標一般情況下是無法直接求得,但交點個數以及所有交點的橫坐標之和可以依據對稱性求出,具體步驟:首先準確作出函數圖象,其次,依據對稱中心或者對稱軸巧妙解決.
此題型升級以后,函數以抽象函數的形式給出,具體圖象無法作出,交點個數也無法確定,此時,必須依據對稱性的一般規律,加以解決.
一、中心對稱型
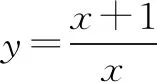
A.0 B.mC.2mD.4m
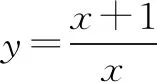
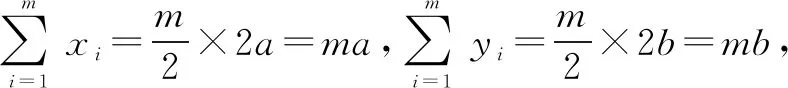
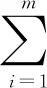
二、軸對稱型
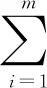
A.0 B.mC.2mD.4m
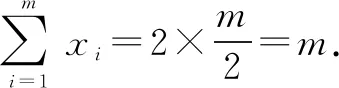
軸對稱型的一般結論:函數y=f(x)與函數y=g(x)的圖象都關于直線x=a軸對稱,兩個圖象交點為(x1,y1),(x2,y2),…,(xm,ym),所有交點關于直線x=a對稱分布,對于每一對對稱點,有x1+x1′=2a,當m為偶數時,