萬變不離其宗 起落皆有定數
——三角函數圖象類問題的圖表對照法例析
趙明丁
(廣東省佛山市順德區第一中學 528300)
一、眾里尋她千百度——撲朔迷離中的困惑
三角函數圖象及性質為高考必考內容,主要考查:
(1)三角函數的最值、周期性、單調性、對稱性等性質;
(2)函數圖形的平移、伸縮、反射變換等;
(3)方程或不等式代數運算等.由于該內容涉及較多公式(包括誘導公式、倍角公式、和差角公式和相關點坐標和相關軸線公式等),而且題型多樣、結構靈活,對學生能力要求較高.亂花漸欲迷人眼,能否“九九歸一”尋求一種通法,以不變應萬變,將它們一網打盡呢?
二、一圖一表總關情——在探索總結中提煉精華
三角函數圖象類的常見題型有:
(1)由函數圖象求其代數表達式進而研究其相關性質;
(2)由函數解析式,研究函數圖象的點坐標、對稱軸或單調區間;
(3)由三角函數性質或圖象,研究參數的值或取值范圍;
(4)三角函數圖象及性質與其它知識的綜合.
題型眾多,能否有統一的解題法?本文提出一種圖表對照法,即利用“一幅圖”和“一張表”對照輔助解題的方法.由于形如y=Asin(ωx+φ)+b或y=Acos(ωx+φ)+b的一般三角函數的圖形都可由基本的正弦函數y=sinx圖象通過一系列坐標變換所得,如果能將題目所研究的三函數的自變量取值以及相關圖形特征都回歸到基本正弦曲線中,用數形結合的思想,問題就簡單明了.以下例析闡釋.
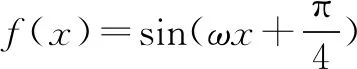
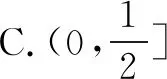
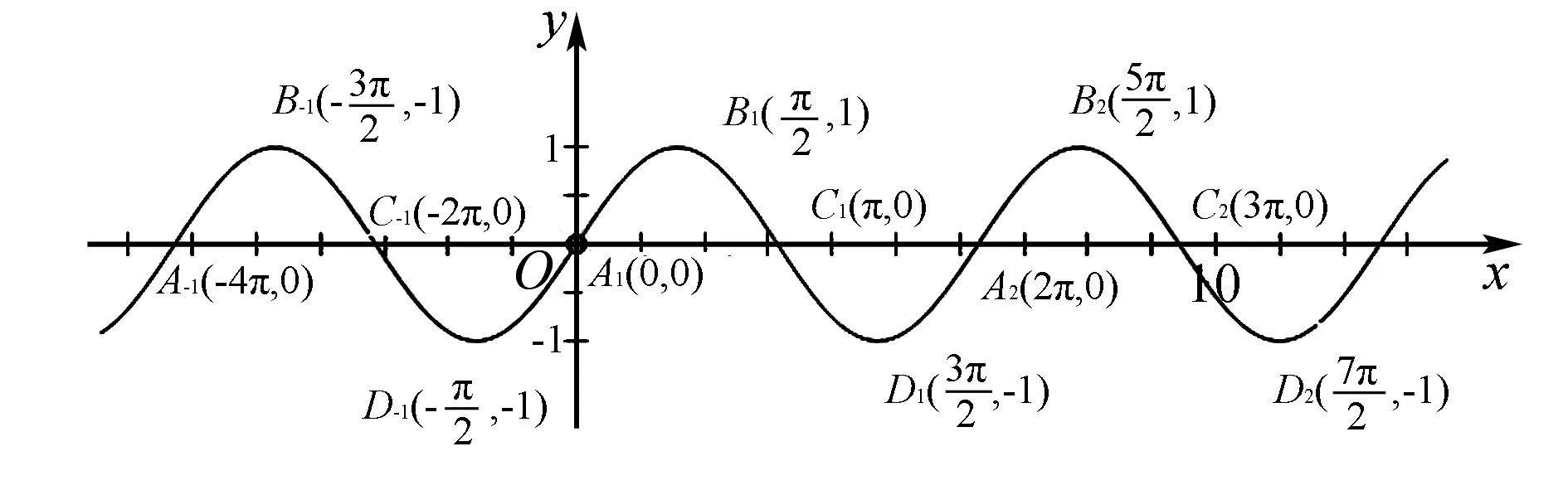
圖1
分析先畫出基本正弦函數圖象,如圖1所示,在圖中A1,B1,C1,D1代表了x軸正方向第一周期的四個關鍵點,下標為2代表第二周期,下標為-1代表負方向第一周期,依次類推,圖象可根據需要向兩邊延展,本文例題將反復使用圖1進行對照研究.接著,在表格中按從小到大的順序列出題中所涉及的自變量x的值,計算括號內的角的對應值X,并寫出各取值與圖1中的圖象的對應位置或相對位置,如表1所示.
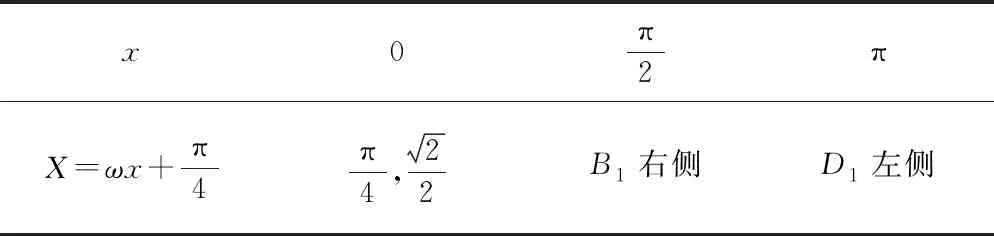
表1

評析上法充分利用了我們最熟悉的基本正弦曲線的直觀圖形輔助解題,同時用表格的形式清晰列出題中涉及的自變量x所有取值(包括參照值0)、括號內的量X的值及他們對應圖1的位置或相對位置,然后根據表格可列出方程或不等式,求解得答案.
三、吹盡黃沙始到金——在解題實戰中升華方法
上例詳細分析了用“圖表對照法”探究三角函數中參數的取值范圍問題,以下將采用該法來解其它題型.
題型1根據三角函數圖象,確定參數的值
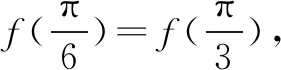
通過與參照點數量比較,只能落在D1處,所以可得表2所示的對應關系.

表2
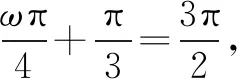
題型2確定三角函數在給定區間中的最值
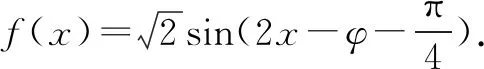

表3
答案為A.
評析本題的解法大多是通過研究周期得到ω的取值范圍,經過計算再求出φ的可能取值,然后再驗證單調
性是否得到滿足,其推理過程比較復雜,如用上法,思維簡化,運算也不復雜,能夠更快、更準地得到答案.
四、映日荷花別樣紅——在反思對比中參透本質
求解三解函數圖象及性質相關的問題時,尤其是客觀題時,“回溯本原”,把三角函數相關問題放在基本正弦曲線上研究,結合圖象和表格確定數量和位置間的對應關系,省去中間較為復雜推理和演算過程.該方法緊扣函數圖象本質,立足知識的”根本”,若能在解題實踐中將本方法靈活應用,必能達到“枝繁葉茂”的效果,體會到這種“圖表對照法”的優越性.

