巧構模型妙解題
王洪信
(甘肅省合水縣第一中學 745400)
新的數學課程標準(2017年版)提出了數學學科核心素養的六個方面,其中之一——數學建模,是數學應用的重要形式,是解決問題的基本手段,也是推動數學發展的動力.構造數學模型解題是一種創造性思維.通過對題設條件和目標的觀察、分析、聯想,根據題目特征,構造出熟知的數學模型來解決問題.這樣往往能化隱為顯,化繁為簡,從而獲得新穎而別具特色的解題方法.
一、構造函數模型

分析不等式結構復雜,不易觀察識別.若記log3x=u,則這是一個關于u的二次不等式,但各系數較為復雜且在變化,不易把控.若改變視角,設log2m=t為主元,則這是簡單的一元一次不等式在定區間上恒成立的問題.
解設log2m=t(0≤t≤1),記log3x=u,關于t整理成f(t)=(u2-6u+1)t+1-u2>0(0≤t≤1)時,求u的取值范圍.
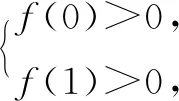
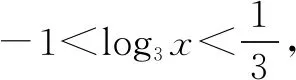
二、構造方程模型
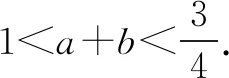
分析可視目標式a+b=t為一整體,從已知式中導出ab關于t的表達式,從而利用熟知的韋達定理之逆,構造出一元二次方程,再用判別式求解.
證明由已知式有(a-b)(a2+ab+b2)=(a-b)(a+b).而a>b?a-b≠0,故有a2+ab+b2=a+b?(a+b)2-ab=a+b.
記a+b=t,則ab=t2-t.由此可知a、b是一元二次方程u2-tu+(t2-t)=0的兩個不等的正根,故有

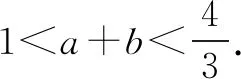
點評解題中要注意兩個不等正根的充要條件,防止僅列出u1+u2>0,u1u2>0,而遺漏Δ>0的錯誤發生.
三、構造不等式模型


Δ=4a2-4(b+1)≤0,且Δ=4a2-4(b+1)≥0.
從而有Δ=0,得a2-b-1=0 ①.
同理由f(x)的最大值是4,可得a2+4b-16=0 ②.
點評本例解答的亮點是一方面將最值轉化為二次不等式恒成立,另一方面又將最值轉化為二次方程有實根,那么既有Δ≤0又有Δ≥0,從而夾逼出Δ=0.本例解答過程中,不斷實施函數、方程、不等式模型間的轉換,體現了思維的靈活與嚴謹.
四、構造數列模型
例4 設0 證明構造數列bn=(1-a1)(1-a2)…(1-an)+(a1+a2+…+an),只要證bn≥1.而 bn+1-bn=-an+1(1-a1)(1-a2)…(1-an)+an+1 =an+1[1-(1-a1)(1-a2)…(1-an)]. 由題設0 所以bn≥b1=(1-a1)+a1=1,從而得 (1-a1)(1-a2)…(1-an)≥1-(a1+a2+…+an). 點評對于形如f(n)>g(n)的數列不等式的證明,常可構造新數列模型F(n)=f(n)-g(n),來證明兩條:①F(1)>0;②F(n)是遞增,由此得到F(n)≥F(1)>0,即f(n)>g(n). 分析從條件等式的分母是1+a2的結構,聯想到三角中的正切代換. 同理得cos2β≥2sinγsinα,cos2γ≥2sinαsinβ. 這三個不等式相乘,可得 (cosαcosβcosγ)2≥8(sinαsinβsinγ)2. 點評本例有多種證法,但由式子的結構特征,引入三角的正切式,簡化了原來的式子,利用熟悉的三角公式模型,迅速獲證. 分析由左端根式中的平方和形式,聯想到向量的模,因此可構造向量模型,再用模的不等式. 例7 設x、y、z∈(0,1),求證x(1-y)+y(1-z)+z(1-x)<1. 分析由條件范圍(0,1),聯想到隨機事件的概率取值范圍,構造概率模型. 從而得x(1-y)+y(1-z)+z(1-x)<1. 點評本例對于數值范圍(0,1)賦于實際意義——隨機事件的概率——投籃的命中率,又結合集合圖形來理解各事件間的關系.本例解法展現了數字模型——概率模型——集合模型間的轉換,方法新穎且易于理解.五、構造三角模型
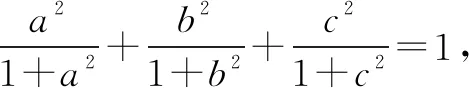

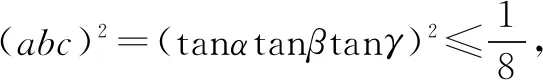
六、構造向量模型


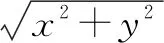
七、構造概率模型