基于裂紋尖端應力比值的含裂紋功能梯度材料圓筒應力強度因子計算方法

李 戎 ，楊 萌 ，梁 斌 ，NODA Nao-Aki

(1. 河南科技大學土木工程學院，河南，洛陽 471023；2. 九州工業大學機械系，日本，北九州市 804-8550)

功能梯度材料圓筒(以下簡稱 FGM 圓筒)是一種可設計性非均勻復合材料結構，因其消除了傳統復合材料結構中存在的界面問題而被廣泛應用于航空航天、汽車、船舶與海洋工程等領域[1-2]。由于FGM圓筒服役期間通常處于極端環境，極易出現裂紋損傷。裂紋的存在不僅會影響結構性能，還有可能導致整個工程結構失效[3]。因此，對含裂紋FGM 圓筒結構進行力學分析是保障工程結構安全性與先進性的先決條件。

裂紋尖端的應力強度因子是確定含裂紋構件安全性的重要參數[4-7]。近年來，已有大量研究論文涉及了這一領域[8-13]，基于權函數法[8-9]、能量釋放率法[12]等方法研究含裂紋FGM圓筒的應力強度因子。已有研究結果顯示，可以將針對含裂紋均勻材料的理論分析方法加以改進，應用于含裂紋FGM圓筒應力強度因子的研究中[8,11]。但是，由于FGM性質的特殊性，FGM結構力學行為比均勻材料結構復雜很多。因此，盡管均勻材料結構應力強度因子已經可由經驗公式得到[14]，FGM 結構應力強度因子計算過程卻仍然難以擺脫復雜矩陣運算和數值積分[8-13,15]。課題組前期研究發現，可以基于參考問題模型與未知問題模型之間的穩定應力關系簡化奇異應力場強度的分析步驟，但是研究對象僅限于膠接結構，且界面端的材料組合以及幾何尺寸需完全相同[16-19]。如果能夠找到均勻材料結構與FGM結構應力強度因子之間存在的穩定關系，便有可能將復雜的FGM結構應力強度因子求解問題轉化為簡單的系數計算以及均勻材料結構應力強度因子經驗公式求解問題。

為此，本文在課題組已有研究[16-19]的基礎上，探尋FGM圓筒與均勻材料圓筒這兩者裂紋尖端應力與應力強度因子之間存在的穩定關系，最終基于裂紋尖端應力比值，提出了一種適用于含環狀裂紋FGM圓筒的應力強度因子高精度快速計算方法。為了適應工程需要、降低計算難度，本文研究時不考慮裂紋尖端非奇異應力的影響[20]。將本文計算結果與參考文獻計算結果進行對比，驗證了本文方法的可行性和優越性。

1 力學模型

采用有限元軟件MSC. Marc Mentat 2012.1.0建立含環狀裂紋FGM圓筒2D軸對稱模型(見圖1)，裂紋深度為a，圓筒長度為2L，厚度為h，內外半徑分別為Ri和Ro，材料沿厚度方向連續性變化，圓筒兩端施加拉力hσ。

圖1 FGM圓筒結構示意圖Fig.1 Dimension for FGM hollow cylinder

2 理論推導

2.1 功能梯度材料

假設功能梯度材料性質沿厚度r′方向按照指數函數分布形式連續性變化[11]，則FGM圓筒內、外表面材料的體積分數之間存在以下關系：

式中：Vi(r′)為內表面材料體積分數；Vo(r′)為外表面材料體積分數；p為材料梯度指數(0 ≤ p ≤ ∞ )。當p=0時，FGM圓筒退化為均勻材料圓筒。

當FGM圓筒由兩種材料組成時，圓筒的材料性質表現為從圓筒內表面材料到圓筒外表面材料性能的連續性變化。基于線性混合法則[21]，圓筒的彈性模量E和泊松比ν可表示為：

式中，Ei和Eo、iν和oν分別為FGM圓筒內外表面材料的彈性模量、泊松比。

2.2 應力強度因子

根據線彈性斷裂力學，通常情況下的FGM結構裂紋尖端應力場表達式如下所示[22]：

式中：i, j = 1 ,2,3對應空間坐標系的三個方向；r和θ為裂紋尖端極坐標(見圖 2)；為無量綱角函數；KI、 KII、 KIII為應力強度因子，與材料梯度、載荷以及幾何尺寸有關。

圖2 圓筒裂紋尖端幾何模型Fig.2 Schematic of crack tip in hollow cylinder

對于圖1所示的兩端施加均勻軸向拉力的含環向裂紋FGM圓柱殼，其所對應的Ⅰ型裂紋尖端應力場可表示為：

材料梯度會影響應力強度因子數值，但是不會影響應力奇異性以及無量綱角函數[23]。因此，理論上可以利用“比例”形式消除奇異性以實現在保證精度的基礎上降低計算難度、簡化計算過程。

無量綱應力強度因子FI和應力強度因子KI滿足關系式：

當FGM圓筒和均勻材料圓筒裂紋受力情況、裂紋類型、裂紋尖端附近網格劃分情況等均相同時，這兩者的裂紋尖端附近應力比值與相應應力強度因子比值之間存在如下關系：

由式(5)和式(6)可知，當FGM圓筒與均勻材料圓筒兩端受力hσ相同時，和裂紋尖端應力σy( r)之間存在如下比例關系：

式中： aFGM和a均勻材料可根據實際情況自由選擇，兩者數值可不相同；為遠距均勻軸向拉伸均勻材料圓筒的無量綱應力強度因子(見式(9))[14]。

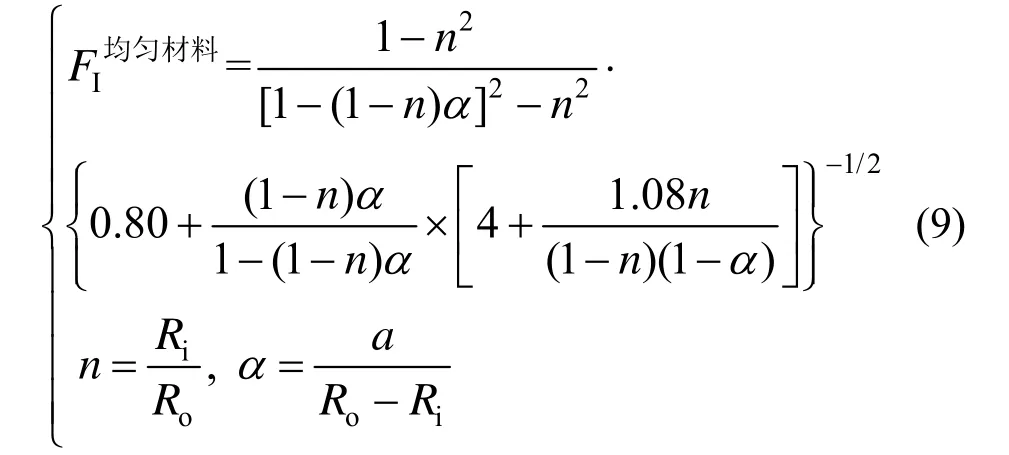
3 算例與討論

建立圖3所示1/4圓筒模型即可滿足計算需求，圓筒兩端施加拉應力hσ=1 MPa，h=1 mm，使用四節點四邊形單元，裂紋尖端附近網格加密，emin=1/38mm、 Ri/Ro=0.8時單元總數為23 289，其中裂紋尖端附近單元數約為20 000。本文中，設定FGM圓筒外表面材料彈性模量Eo數值固定，內表面材料彈性模量Ei可變。假設泊松比為常數，ν=0.3。當

o/i

E E=1時，FGM退化為均勻材料。

圖3 模型網格劃分示意圖Fig.3 Mesh pattern for model

3.1 裂紋尖端應力分布

FGM圓筒外表面材料體積分數Vo沿厚度方向隨體積函數冪指數p變化(見圖4)，其可設計性可以通過控制內外兩種材料組分比例實現[24]，Vo=1-Vi。當p≤0.2或p≥10時，大部分Vo值接近1或者0。以p≥10為例，雖然材料性能仍然由內表面材料沿厚度方向連續性變化至外表面材料，但Vo初始變化幅度非常小，圓筒內側材料對材料性能起主導作用；靠近筒外壁時，Vo變化幅度接近最大。

圖4 FGM圓筒外表面材料沿厚度方向體積分數Vo Fig.4 Variation of volume fraction of outside material Vo of FGM hollow cylinder in the thickness direction

由于裂紋尖端奇異性的存在，使用 Marc得到的應力值yσ不僅受圓筒材料性質影響，還會隨裂紋尖端附近最小網格尺寸emin以及裂紋尖端距離r的改變而發生變化(見圖 5)，不能直接使用。當h/ L ≥ 5 時，h/L對應力值的影響可以忽略不計。圓筒幾何參數為：L/h＞5，Ri/Ro=0.8，a/h=0.1。

圖5 材料性質和emin對裂紋尖端應力分布的影響Fig. 5 The influences of material property and emin on the stress distribution at crack tip

當FGM圓筒與均勻材料圓筒厚度、載荷工況以及裂紋尖端附近網格劃分等完全相同、emin又小到一定程度時，兩者裂紋尖端應力比值穩定，可以通過比值形式消除應力奇異性。

由表 1中的 a)～b)可見，當 h / L ≥ 5 、emin=1/34mm時，裂紋端部應力值隨r/h增大而減小，應力比值變化幅度較大。當emin=1/38mm時，應力值仍然隨r/h增大而減小，但是已經基本恒定不變；表1中的c)，FGM 圓筒L/h=2，均勻材料圓筒仍然使用h/ L ≥ 5 。結果顯示，應力比值變化規律與表1中的a)～b)中應力變化情況相同，仍然在emin=1/38mm時達到穩定狀態，并未受到筒體長度影響。因此，可以使用應力比值進行應力強度因子計算，并且僅使用裂紋尖端節點應力值 σy0,FEM[16]即可滿足計算需求，此結論與文獻[16—19]相同。下文中，應力值σy均為σy0,FEM。

表1 不同網格尺寸時裂紋尖端應力分布)Table 1 Stress distributions for crack tip obtained by different mesh sizes (Ri /Ro = 0 .8, ( E o / E i ) F GM= 0 .4) of

表1 不同網格尺寸時裂紋尖端應力分布)Table 1 Stress distributions for crack tip obtained by different mesh sizes (Ri /Ro = 0 .8, ( E o / E i ) F GM= 0 .4) of

a) / 5 L h≥ ,/ 0.1 a h= ofe = 1/38 mm min e = 1/34 mm min FGM ya/h0.1 σ = /σ均勻材料= /FGM y / 0.1 ya/h0.1σ σ FGM y / 0.1 r/h σ = /MPa均勻材料 r/h= =σ均勻材料= /FGM ya/h0.1ya/h0.1均勻材料MPa MPa y / 0.1 ah ah MPa σ σy / 0.1 ah ah= =→0 25.5710 41.719 0.613 →0 2.8120 4.5687 0.615 1/ 3812.7970 20.870 0.613 1/34 1.5169 2.3967 0.633 2/ 38 9.3436 15.233 0.613 2/34 1.1916 1.8388 0.648 3/ 38 7.4826 12.194 0.614 3/34 1.0298 1.5511 0.634 4/ 38 6.4610 10.525 0.614 4/34 0.9538 1.4049 0.679 b) / 5 L h≥ , / 0.8 ah= (FGM), / 0.1 ah= (均勻材料)e = 1/38 mm min e = 1/34 mm min σ σ σ = /FGM ya/h0.8σ均勻材料= /ya/h0.1σ σ FGM y a/h 0.8 ah= =σ = /MPa ofr/h ofr/h FGM ya/h0.8σ均勻材料= /ya/h0.1 FGM y / 0.8均勻材料 均勻材料MPa ofMPa ofy / 0.1 ofMPa ofy / 0.1 ah ah= =→0 251.070 41.719 6.01 →0 27.8580 4.5687 6.10 1/ 38 125.520 20.870 6.01 1/3413.8180 2.3967 5.77 2/ 38 91.548 15.233 6.01 2/34 9.9266 1.8389 5.40 3/ 38 73.230 12.194 6.01 3/34 7.7770 1.5511 5.01 4/ 38 63.160 10.525 6.01 4/34 6.5358 1.4049 4.65 c) / 2(FGM), / 5( )Lh Lh=＞ 均勻材料 ofe = 1/38 mm min e = 1/34 mm min σ = /σ均勻材料= /ya/h0.1 FGM ya/h0.1σ = / ofMPa ofσ σ FGM y / 0.1均勻材料 ofr/h ofr/h= =σ均勻材料= /FGM ya/h0.1ya/h0.1均勻材料MPa FGM y / 0.1 MPa σ σy / 0.1 ah ah MPa y / 0.1 ah ah= =→0 33.9930 41.719 0.815 →0 3.7346 4.5687 0.817 of1/ 38 17.0100 20.870 0.815 1/34 2.0012 2.3967 0.835 of2/ 38 12.4190 15.233 0.815 2/34 1.5608 1.8389 0.849 of3/ 38 9.9442 12.194 0.815 3/34 1.3385 1.5511 0.863 of4/ 38 8.5856 10.525 0.816 4/34 1.2305 1.4049 0.876 of

本文中，emin=1/38mm已經可以滿足計算需求。若進一步細化網格，采用更小的emin，單元數量明顯增多，運算時間隨之延長，但對計算結果基本沒有影響。因此，不宜過度細化網格。

3.2 應力強度因子計算

求解時，由式(8)可得含裂紋均勻材料圓筒無量綱應力強度因子，再將由 Marc得到的裂紋尖端應力值代入式(9)即可得到含裂紋FGM圓筒無量綱應力強度因子，具體計算結果見表2。圓筒幾何參數為： L / h ≥ 5 ， Ri/ Ro=0.8。

表2 無量綱應力強度因子計算Table 2 Calculation of dimensionless stress intensity factor F ⅠFGM

表2 無量綱應力強度因子計算Table 2 Calculation of dimensionless stress intensity factor F ⅠFGM

含裂紋均勻材料圓筒 of 含裂紋FGM圓筒(o/i E E=0.4, p=1) ofa / h ofyσ均勻材料/ ofF均勻材料FGM yσ/ ofI F ofa/h ofMPa ofFGM I F MPa ofF均勻材料 FGM I I 0.1 of 25.572 of 0.6130 of 0.6959 0.2 of 41.556 of 0.7044 of 0.7996 0.3 of 59.597 of 0.8248 of 0.9363 0.1 of 41.719 of 1.1352 of0.4 of 81.484 of 0.9766 of 1.1087 0.5 of 108.800 of 1.1663 of 1.3240 0.6 of 143.400 of 1.4033 of 1.5931 0.7 of 188.400 of 1.7069 of 1.9378 0.8 of 251.070 of 2.1277 of 2.4155

圖6中針對FGM圓筒長厚比L/h、筒體內外半徑比 Ri/ Ro、裂紋深度與圓筒壁厚比a/h、FGM性質(內外表面材料彈性模量比 Eo/Ei，材料梯度指數 p)等影響因素，將本文方法計算結果與參考文獻[11—12]結果進行對比了分析。從中可以看出，本文計算方法結果與文獻計算結果吻合度較好，驗證了本文方法的正確性和有效性。

文獻[12]中，材料常數 γ = Eo/Ei= eβ，彈性模量 E (r′ ) =。

本文方法是基于裂紋尖端應力比值，而文獻采用位移有限元法、柔度法、有限差分法等方法，計算方法的不同是造成誤差的主要原因。由圖3可知，FGM圓筒材料性質沿厚度方向隨冪指數p變化。當p=10時，靠近筒外壁處(a/h=0.1)Vo值變化幅度很大，對計算結果影響較為明顯。FGM圓筒內、外表面材料性質差異較大時，p影響更為顯著。

圖6 無量綱應力強度因子對比分析Fig.6 Comparison of dimensionless stress intensity factor

由圖7可見，近90%的本文計算結果與參考文獻計算結果之間的誤差小于 4%，僅有一處數據誤差值超過7%。當h/L＜5、 a / h ≥ 0 .2時，誤差接近0%(見圖7)。當γ減小或 Eo/Ei增大時，誤差有增大趨勢，但最大誤差可控制在6.5%以內。選取較大誤差位置所對應參數進行校核( Eo/Ei=10、p=10、a/h=0.6)，計算結果=1.9067，參考文獻計算結果為1.9725，誤差為-3.3367%，仍保持在合理范圍內。殼體參數類型改變時，計算誤差也并未出現明顯的規律性變化，計算結果穩定。

圖7 計算誤差對比分析Fig.7 Comparison of calculation errors

表3 對計算結果的影響Table 3 The effect of on the results of

表3 對計算結果的影響Table 3 The effect of on the results of

含裂紋F GM圓筒 of/=2 E E ,p=10,i/o=0.8含裂紋均勻材料圓筒 ofL h≥ ，o/i=10/ 5 R R ,L h ,γ=2,i/o=0.5 R R , ofFGM FⅠ =1.973 [12] ofFGM FⅠ =1.352[11] ofa/h yσ均勻材料F均勻材料 a/h FGM yσ/FGMyσ/I F ofa/h ofFGM I FFGMI/MPa ofMPa ofMPa of0.1 41.72 1.135 1.907 1.440 0.2 63.65 1.171 1.823 1.377 0.3 85.55 1.228 1.742 1.315 0.4 109.40 1.310 1.677 1.267 0.5 136.40 1.426 1.638 1.237 0.6 167.80 1.596 1.632 1.233 0.7 206.00 1.855 1.670 1.261 0.8 258.20 2.303 0.6 171.60.1 52.92 1.7681.335

由于本文計算方法基于裂紋尖端應力比值，裂紋尖端附近網格劃分需滿足要求，需細化至裂紋尖端附近應力比值基本穩定不變時再進行計算，且FGM 圓筒與均勻材料圓筒裂紋尖端附近網格劃分必須一致。

與文獻中使用的計算方法相比，本文計算方法避免了復雜的矩陣運算以及數值積分，計算精度高，計算量小，適用范圍廣。計算時，均勻材料圓筒可由經驗公式獲得，過程簡便，適合工程應用。本文方法不僅適用于含外表面環狀裂紋FGM圓筒，還可用于其他裂紋形式的FGM結構的應力強度因子計算，但是現有研究結果還很有限，本項目后續工作將進行深入研究。

4 結論

本文基于FGM圓筒與均勻材料圓筒裂紋尖端應力值與應力強度因子之間的穩定比例關系，提出了一種適用于含外表面環狀裂紋的FGM圓筒應力強度因子計算方法。該方法在保證精度的基礎上成功避免了復雜的矩陣運算和數值積分，僅通過使用含環狀裂紋均勻材料圓筒應力強度因子經驗公式、FGM圓筒與相應均勻材料圓筒裂紋尖端應力比值，即可得到FGM圓筒應力強度因子，計算過程簡單。計算結果顯示，本文方法適用于不同FGM類型、圓筒尺寸以及裂紋深度時的應力強度因子計算，計算時所用的可任意選取，且僅需計算一次即可滿足不同情況下的計算需求，計算精度高、結果穩定，便于工程應用。