基于勁度模量分析的橡膠瀝青混合料疲勞壽命研究

房辰澤，郭乃勝，孫雅珍，王金昌

(1. 大連海事大學交通運輸工程學院，遼寧，大連 116026；2. 沈陽建筑大學交通工程學院，遼寧，沈陽 110168；3. 浙江大學交通工程研究所，浙江，杭州 310058)

瀝青路面結構長期處于外部荷載重復作用之下，材料結構萌生損傷并持續演化導致材料強度逐步衰減，材料強度的衰減同時加速損傷演化。材料強度在損傷演化至失效閥值時低于外部荷載，最終導致路面結構發生疲勞破壞[1-5]。因此，基于強度衰減規律研究瀝青混合料的損傷演化過程并準確預測疲勞壽命，對于延長瀝青路面疲勞壽命至關重要[6-11]。

國內外學者基于全部衰減的勁度模量均對材料產生損傷變形的假定，將勁度模量的衰減值與初始值的比值作為損傷變量，并將相應的損傷曲線作為疲勞性能評價及壽命預測的重要理論依據[12-14]。Sousa等[15]通過開展瀝青混合料不同試驗條件下的室內疲勞試驗捕捉了勁度模量取值的分布規律，為基于材料的強度衰減規律掌握其疲勞特性以及建立科學的疲勞方程提供了理論依據。Rowe和Bouldin[16]通過統計材料疲勞失效對應的勁度模量分布規律，基于該分布規律率建立了瀝青混合料的疲勞方程。Robert等[17]根據材料勁度模量衰減規律捕捉疲勞失效閾值，提出了考慮瀝青混合料溫度影響的疲勞試驗統計方法。Léonard和 Benedetto等[18-19]分別采用經典損傷力學和連續損傷力學對瀝青混合料的疲勞性能進行了研究并建立了損傷模型，為開展材料疲勞損傷在不同試驗條件下的非線性演化過程研究提供了理論基礎。呂松濤[20]通過對梁式拉伸疲勞試驗采用模量衰減定義損傷變量，完善了瀝青路面的軸載換算方法。欒利強和田小革[21]通過研究瀝青混合料的非線性損傷演化特征，建立了耦合間歇時間、溫度、應力比等試驗因素的非線性損傷模型，并推導出試件結構的疲勞壽命和材料臨界損傷因子之間的數學關系。Sun等[22]通過三點彎曲疲勞試驗提出了勁度模量衰減數學模型，并基于非線性損傷演化分析建立了疲勞損傷本構方程和耦合多因素疲勞方程。

另外，部分研究學者從永久變形和能量耗散方面開展系統深入的研究，指出只有部分衰減的勁度模量會對瀝青混合料產生疲勞損傷變形，剩余部分對用于產生黏彈性變形，這為基于勁度模量衰減規律進行損傷演化分析提供了新思路[23-28]。因此，上述文獻中基于所有衰減勁度模量用于產生損傷變形假定得到的損傷變量，不能深刻地揭示材料疲勞破壞前的損傷演化過程，相應的壽命預測結果和試驗結果之間有較大的離散性。為此，本文對不同溫度、應力比及加載速率等疲勞試驗條件下的橡膠瀝青混合料疲勞壽命與勁度模量衰減規律的相關性開展系統深入的研究，采用累積勁度模量衰減量相對變化率定義損傷并開展相應的損傷演化分析，基于勁度模量衰減量相對變化率與材料損傷演化速率的相關性分析建立疲勞方程預測壽命，并與試驗結果對比驗證該疲勞方程的準確性。

1 材料和試驗方法

1.1 材料

選用橡膠瀝青開展三點彎曲疲勞試驗，測試獲得的指標結果如表1所示。集料級配類型為AC-13I型，如表2所示。

表1 橡膠瀝青技術性能Table 1 Technical properties of asphalt rubber

表2 集料級配Table 2 Aggregate gradation

1.2 試件制備

依據《公路工程瀝青及瀝青混合料試驗規程》(JTG E20—2011)規定的車轍板試件制備流程(T0703)，車轍板試件對應的成型尺寸為 300 mm×300 mm×70 mm，并標注成型方向，靜置時間 12 h后進行拆模。采用切割機沿著成型方向將兩側邊緣20 mm 的部分切除，然后切出尺寸為 250 mm×30 mm×35 mm的梁式試件，制備的小梁試件如圖1所示。

圖1 小梁試件Fig.1 Beam specimens

1.3 試驗方法

選取小梁頂部中央位置作為三點彎曲疲勞試驗的測試區域，疲勞試驗機壓頭作用于測試區域，并通過自動采集系統獲得測試區域不同時刻的力和位移數據，通過結構力學梁式試件的彎拉求解公式獲得小梁底部中央的拉應力和拉應變。

為便于分析應力比、溫度、加載速率對三點彎曲疲勞試驗結果的影響，設置如表3所示的6組對比試驗。梁式試件支座跨徑為 200 mm。疲勞加載程序由以下三部分組成：1) 按照設定的加載速率勻速加載至不同應力比對應的峰值荷載；2) 按照設定的加載速率勻速卸載至荷載為0；3) 返回1)。

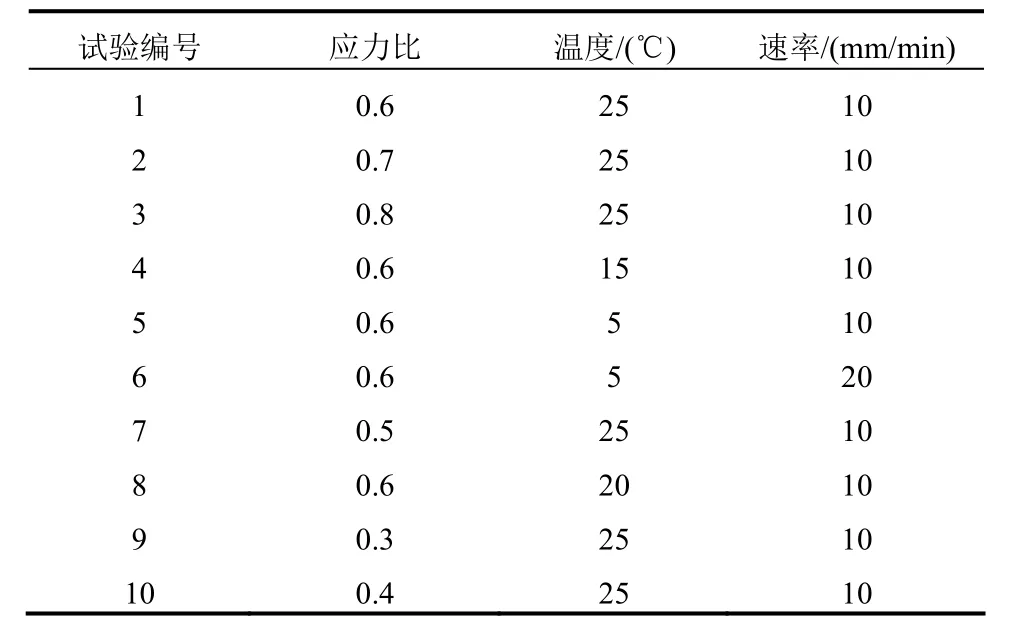
表3 試驗條件Table 3 Test conditions

試驗步驟如下：1) 把小梁放于設定溫度的恒溫水槽 1 h，啟動疲勞試驗加載室的控溫系統，將加載室與水槽保持一致；2) 將支座準確對中固定，并保證兩支點間距為 200 mm，將試件取出對稱放置于支座上；3) 啟動如圖2所示的疲勞試驗機按照疲勞加載程序對小梁試件進行循環加載，直至試件發生斷裂。

圖2 疲勞試驗機Fig.2 Fatigue testing machine

2 結果分析

2.1 三點彎曲疲勞試驗

由于材料本身的黏彈滯后特性，循環荷載對應的應力-應變曲線呈滯后閉路形狀，典型橡膠瀝青混合料每個循環對應的應力-應變曲線如圖 3(便于清晰展示，只給出4個循環)所示。由圖3可知，隨著材料應變的不斷增大，材料所受拉應力在加載階段非線性增大至峰值，且疲勞破壞前每個循環的應力峰值相同，進入卸載階段后拉應力逐漸減小至0。

當疲勞次數達到一定次數后，小梁結構不能承受設定的荷載幅值從而發生斷裂。發生斷裂時對應的循環次數記為疲勞壽命Nf，Nf的試驗結果如表4所示。由表4可知，Nf與速率和應力比負相關，與試驗溫度正相關。

圖3 三點彎曲疲勞試驗應力-應變曲線Fig.3 Stress-strain curve of three-point bending fatigue test

表4 疲勞壽命結果Tab 4 Results of fatigue life

2.2 橡膠瀝青混合料疲勞壽命與勁度模量衰減規律的相關性分析

小梁底部中央位置受拉狀態下的應力和應變之比為材料的勁度模量。由圖3可以看出，每個循環對應的拉應力峰值一樣，但材料在拉應力峰值處承受的拉應變卻隨著損傷演化的進行逐漸增加，這導致了荷載峰值處的勁度模量不斷地發生衰減。選取荷載峰值處的勁度模量為研究對象，分析疲勞壽命與勁度模量衰減規律的相關性，為損傷演化分析提供理論依據。

2.2.1 橡膠瀝青混合料不同階段的材料特性

橡膠瀝青混合料損傷和未損傷階段的應力-應變曲線如圖4所示。由圖4可知，不同應變水平下材料特性的變化過程由未損傷階段OD(包括線性黏彈性階段OB和非線性黏彈性階段BD)和損傷階段DE 組成[27—30]。

圖4 橡膠瀝青混合料不同階段的應力-應變曲線Fig.4 Stress-strain curve of different material states of rubber asphalt mixture

未損傷階段：線性黏彈性階段對應的加載路徑OA和卸載路徑AO相同，線性黏彈性變形在卸載之后完全恢復，該階段勁度模量不變且材料不產生損傷變形。非線性黏彈性階段對應的加載路徑 OBC和卸載路徑CO不同，非線性黏彈性變形在卸載之后完全恢復，該階段勁度模量衰減但材料不產生損傷變形；損傷階段：加載路徑 OBDE和卸載路徑EF不同，黏彈性變形在卸載之后理論上可以完全恢 復但損傷變形不能恢復，勁度模量在該階段發生衰減且材料產生損傷變形[27-30]。

基于以往的研究可知，材料在進入疲勞損傷狀態之后，只有部分衰減的勁度模量用于產生橡膠瀝青混合料對應的損傷變形，為基于勁度模量衰減規律的Nf預測提供了理論依據[23-28]。

2.2.2 疲勞壽命與勁度模量衰減量的相關性分析

橡膠瀝青混合料初始勁度模量與各循環勁度模量的差值為勁度模量衰減量 SMD(stiffness modulus degradationa)，如圖5所示，圖中循環比等于(N/Nf)。由圖5(a)可知，三種應力比下，SMD和Nf對應的大小排序依次為0.7、0.8、0.6和0.6、0.7、0.8；由圖5(b)可知，三種溫度下SMD和Nf對應的大小排序依次為15℃、5℃、25℃和25℃、15℃、5℃；由圖 5(c)可知，兩種加載速率下 SMD和 Nf對應的大小排序依次為20 mm/min、10 mm/min和10 mm/min、20 mm/min。

由上述分析知，隨著SMD的增加，Nf未呈單調變化的趨勢，這是因為循環荷載作用下SMD一部分用于對橡膠瀝青混合料產生損傷變形，剩余部分用于對產生黏彈性變形[23—28]，故應用SMD不能很好地預測Nf。

2.2.3 疲勞壽命與勁度模量衰減量相對變化率的相關性分析

為了更好地揭示SMD與Nf的關系，本研究提出勁度模量衰減量相對變化率 SMDR (stiffness modulus degradation ratio)如式(1)所示，其表明特定條件下每次荷載循環中用于黏彈性變形部分的SMD是一個定值[23-26]，SMDR的大小表征了一次循環加載過程中對橡膠瀝青混合料產生損傷變形的SMD占該循環總SMD的比例，數值越大，表示該循環產生損傷變形的SMD比例越大。

式中，SMDN+1和SMDN分別為第(N+1)和N個循環的勁度模量衰減量。

圖5 不同試驗條件下的勁度模量衰減量Fig.5 Stiffness modulus degradation under different test conditions

不同試驗條件的SMDR如圖6所示，由圖6(a)可知，三種應力比下SMDR和Nf對應的大小排序依次為0.8、0.7、0.6和0.6、0.7、0.8；由圖6(b)可知，三種溫度下SMDR和Nf對應的大小排序依次為5℃、15℃、25℃和25℃、15℃、5℃；由圖6(c)可知，兩種加載速率下 SMDR和 Nf對應的大小排序依次為20 mm/min、10 mm/min 和 10 mm/min、20 mm/min。

由上述分析知，隨著SMDR的增加，Nf總體呈下降趨勢，故SMDR可以用以Nf預測，這亦為后續應用SMDR進行損傷演化分析提供了理論基礎。

圖6 不同試驗條件下的勁度模量衰減量相對變化率Fig.6 Stiffness modulus degradation ratio under different test conditions

3 基于SMDR的橡膠瀝青混合料損傷演化分析

將前N個循環對應的SMDR之和定義為第N個循環的累積勁度模量衰減量相對變化率 CSMDR(cumulative stiffness modulus attenuation ratio)，并根據CSMDR分別建立CSMDR與疲勞次數的函數關系式和損傷模型，為預測Nf提供理論依據。

3.1 CSMDR與疲勞次數函數關系式建立

3.1.1 CSMDR與疲勞次數函數關系式建立

橡膠瀝青混合料損傷演化過程伴隨著 SMDR的累積，掌握CSMDR的變化規律可以為損傷演化分析提供理論依據。CSMDR-N/Nf曲線如圖7所示，由圖 7可知，隨著循環荷載的不斷累積，CSMDR呈現出非線性單調遞增的變化規律。BlNeld模型可以準確地刻畫循環荷載作用下橡膠瀝青混合料CSMDR的非線性變化趨勢，使用該模型建立CSMDR與疲勞次數的函數關系式[22-25]，如式(2)所示。使用式(2)擬合不同試驗條件下的CSMDR -N/Nf曲線，擬合參數結果如表5所示。由表5可知，R2均大于0.99，反映了該關系式的可靠性。

圖7 橡膠瀝青混合料CSMDR-N/Nf曲線圖Fig.7 Fitting result of CSMDR-N/Nf curve of rubber asphalt mixture

式中：CSMDRN為第N循環對應的CSMDR；a、b、c、d為擬合參數；CRN=N/Nf。

表5 模型參數擬合結果Table 5 Fitting results of model parameters

3.1.2 函數關系式驗證

為驗證式(2)的可靠性，選擇基質瀝青混合料補充試驗條件(應力比-溫度-速率)為 0.6-25℃-10 mm/min對應的小梁疲勞試驗。使用式(2)求解相應的CSMDR-N/Nf曲線并與試驗結果對比，對比結果如圖8所示。由圖8可知，建立的函數關系式可以準確地刻畫CSMDR隨疲勞次數的變化特征。

圖8 基質瀝青混合料CSMDR-N/Nf曲線對比圖Fig.8 Comparison of fitting result of CSMDR-N/Nf curveof base asphalt mixture

3.2 損傷模型的建立

3.2.1 損傷模型建立

每個循環產生損傷變形的SMD比例隨著該循環SMDR的增大而增大，故SMDR可視為橡膠瀝青混合料抗損傷變形的不利參數。基于以往的研究可知，前N次與前Nf次循環內抗損傷變形不利參數之和的比值(CSMDRN與 CSMDRNf的比值)表征了第N次循環的損傷因子大小[20-24]，故本文損傷定義如下式所示：

式中：D為疲勞次數為N時的損傷因子；CSMDRN和CSMDRNf分別為疲勞次數為N和Nf時的累積勁度模量衰減量相對變化率。

聯立式(2)和式(3)建立損傷模型，如式(4)所示。使用式(4)擬合不同試驗條件下的 D-N/Nf曲線，R2均大于0.99，證明了該關系式的可靠性。

3.2.2 損傷模型的驗證

為驗證該損傷模型的正確性，使用式(4)求解基質瀝青混合料的D-N/Nf曲線并與試驗結果對比，對比結果如圖9所示。由圖9可知，建立的損傷模型可以準確地刻畫瀝青混合料在循環荷載作用下的的損傷演化過程。

3.3 損傷演化分析

求得 D-N/Nf曲線的斜率作為瀝青混合料的損傷演化速率 D′，繪制三維損傷演化曲線(D′-D-N/Nf曲線)，如圖10所示。由圖10可知，循環荷載作用下橡膠瀝青混合料的損傷演化速率 D′和損傷值 D隨疲勞次數的增加，呈非線性變化趨勢。

圖9 基質瀝青混合料D-N/Nf曲線對比圖Fig.9 Comparison of D-N/Nf curve of base asphalt mixture

圖10 三維損傷演化曲線Fig.10 3D damage evolution curve

將 D′-D-N/Nf曲線進行平面投影，分別得到D-N/Nf曲線、D′-N/Nf曲線、D′-D曲線，如圖11所示。由圖11可知，隨著疲勞次數的增加，損傷值D由0非線性逐漸演化至1；隨著疲勞次數和損傷值D的增加，損傷演化速率D′由較高的速率水平非線性逐漸變化至較低的速率水平。為了更準確地掌握橡膠瀝青混合料的損傷演化規律，將三維損傷演化曲線進行放大，如圖12所示。由圖12可知，D′在疲勞加載的后期階段急劇增大。

根據上述分析可知，循環荷載作用下橡膠瀝青混合料的非線性損傷演化過程分為三個階段：第一階段，損傷快速增長的初始演化階段，D′逐漸變慢，此過程不長但是造成的損傷較大；第二階段，損傷緩慢增長，D′變化幅度較小，該階段占據著損傷演化過程的主要部分；第三階段，損傷在最后階段驟增，D′急劇增加，材料發生疲勞破壞。

圖11 三維損傷演化曲線投影圖Fig.11 Projection of 3D damage evolution curve

圖12 三維損傷演化曲線投影放大圖Fig.12 Projection amplification of 3D damage evolution curve

4 基于SMDR的橡膠瀝青混合料疲勞壽命預測

通過 SMDR與D′的相關性分析建立疲勞方程并預測Nf，為基于勁度模量衰減規律預測橡膠瀝青混合料的Nf提供理論依據。

4.1 SMDR與D′的相關性分析

D′-SMDR-N/Nf曲線投影圖如圖 13所示，由D′-N/Nf曲線和 SMDR-N/Nf曲線可知，隨著疲勞次數的增加，D′和SMDR的取值均呈“兩頭大，中間小”的分布規律；由D′-SMDR曲線可知，隨著SMDR的增加，D′的取值水平整體上呈現出線性遞增的變化趨勢。由此可知，SMDR是表征橡膠瀝青混合料損傷演化快慢的一個物理參數，隨著SMDR的增大損傷變量越快地演化至失效閾值，Nf越小[23—26]，故Nf與SMDR的整體取值水平存在負相關的函數關系。

圖13 D′-SMDR-N/Nf曲線投影圖Fig 13 Projection of D′-SMDR-N/Nf curves

4.2 橡膠瀝青混合料疲勞方程建立

4.2.1 疲勞方程的建立

根據SMDR三個階段內ΔN/Nf的大小決定每個階段的權重，處理試驗數據得到SMDR三個階段的加權平均值 WA(weighted average)，采用 WASMDR代表SMDR三個階段的整體取值水平。

WASMDR的統計結果如表6所示。由表6可知，隨著 WASMDR的增加，Nf呈冪函數下降趨勢。由于冪函數結構簡單易于推廣，故采用冪函數建立如式(5)所示的疲勞方程，R2＞0.97，證明了該疲勞方程的可靠性。

Nf=3.10123(WASMDR)-0.89585，R2=0.976 (5)式中：Nf為疲勞壽命；WASMDR為勁度模量衰減量相對變化率加權平均值。

4.2.2 疲勞方程的驗證

為驗證基于表6中Nf與WASMDR之間冪函數關系建立的疲勞方程，可用于其他試驗條件下的疲勞壽命預測，補充試驗編號分別為7和8對應的橡膠瀝青混合料小梁疲勞試驗并統計 WASMDR。將統計的WASMDR代入式(5)計算Nf并與試驗結果對比，對比結果如表 7所示，由表 7知相對誤差分別為8.705%和9.796%，滿足工程要求。

表6 WASMDR的統計結果Table 6 Statistical results of WASMDR

表7 疲勞壽命結果對比Table 7 Comparison of fatigue life results

為進一步驗證該疲勞方程的可靠性，通過瀝青路面現場鉆取板塊試件獲得相應的橡膠瀝青混合料小梁試件，補充試驗編號分別為9和10對應的現場疲勞試驗，并將對應的WASMDR代入式(5)計算Nf并與試驗結果對比，對比結果如表7所示。由表7可知，相對誤差分別為13.626%和11.356%，滿足工程要求，因此，建立的疲勞方程可以較準確地預測橡膠瀝青混合料的Nf。

由于不同種類瀝青混合料的疲勞損傷特性存在差異，SMDR是否適用于其他類型瀝青混合料的損傷演化分析和疲勞壽命預測，尚需基于大量室內及現場試驗數據開展系統研究作為理論支撐。

5 結論

隨著疲勞荷載次數的增大，勁度模量衰減量SMD呈單調遞增的非線性變化趨勢，循環荷載作用下只有一部分SMD用于對橡膠瀝青混合料產生損傷變形，剩余部分用于對產生黏彈性變形，應用SMD不能很好地預測疲勞壽命Nf。

勁度模量衰減量相對變化率 SMDR表征了產生損傷變形的 SMD 占總 SMD 的比例。Nf隨著SMDR的增大而減小，SMDR可以用于橡膠瀝青混合料的損傷演化分析和預測Nf。

建立的累積勁度模量衰減量相對變化率CSMDR與疲勞荷載次數的函數關系式，可以準確地刻畫CSMDR的非線性單調遞增變化特征，且基于該函數關系式建立的損傷模型可以準確地表征橡膠瀝青混合料的非線性損傷演化規律。

隨著SMDR的增大，損傷變量迅速地演化至失效閾值，Nf越小。基于SMDR加權平均值與Nf之間的冪函數關系建立的疲勞方程，能夠較準確地預測橡膠瀝青混合料的Nf。SMDR是否適用于其他類型瀝青混合料的損傷演化分析和疲勞壽命預測有待進一步研究。