采用通用有限元程序的彌散裂縫模型和分層殼單元模擬鋼筋混凝土構(gòu)件裂縫寬度

陶慕軒，趙繼之

(1. 清華大學(xué)土木工程系土木工程安全與耐久教育部重點實驗室，北京 100084；2. 清華大學(xué)北京市鋼與混凝土組合結(jié)構(gòu)工程技術(shù)研究中心，北京 100084)

裂縫寬度驗算是混凝土結(jié)構(gòu)正常使用極限狀態(tài)驗算的重要內(nèi)容之一。對于一些受力條件單一、邊界條件明確的簡單鋼筋混凝土構(gòu)件(譬如：鋼筋混凝土軸心受拉構(gòu)件、鋼筋混凝土受彎構(gòu)件等)，過去的許多研究以及規(guī)范都建議了半經(jīng)驗半理論的裂縫寬度簡化計算公式[1]。然而，在實際結(jié)構(gòu)體系中，混凝土結(jié)構(gòu)構(gòu)件的內(nèi)力狀態(tài)和邊界條件都比較復(fù)雜，構(gòu)件類型也十分豐富(尤其是近年來，許多新型鋼-混凝土組合構(gòu)件以及新材料-混凝土組合構(gòu)件不斷涌現(xiàn))，亟需發(fā)展更為通用的混凝土裂縫寬度計算方法以適應(yīng)各類混凝土結(jié)構(gòu)構(gòu)件正常使用極限狀態(tài)的驗算需求。

有限元方法是目前結(jié)構(gòu)工程設(shè)計和研究中應(yīng)用最普遍的數(shù)值方法，采用有限元方法計算結(jié)構(gòu)構(gòu)件中混凝土的裂縫寬度不僅通用性強，也易于被結(jié)構(gòu)工程師所接受。經(jīng)典的彌散裂縫模型(Smeared Crack Model)以及Bazant和Oh[2]于1983年提出的裂縫帶理論(Crack Band Theory)為采用有限元方法進行混凝土裂縫分析提供了重要的理論基礎(chǔ)，至今，已有大量學(xué)者基于這些理論背景采用基于彌散裂縫模型的通用有限元程序(例如：ABAQUS、MSC.MARC、ANASYS等)開展了一系列豐富的混凝土裂縫分析的實踐，然而，這些實踐幾乎均以“開裂應(yīng)變”作為最終結(jié)果的展示[3—10]，雖然能夠定性地描述混凝土結(jié)構(gòu)構(gòu)件的開裂程度以及裂縫分布情況，但卻無法定量地給出裂縫寬度值，不僅使計算結(jié)果的準(zhǔn)確性難以得到定量的檢驗，也無法滿足結(jié)構(gòu)設(shè)計規(guī)范中“裂縫寬度驗算”的需求。此外，在分析中如何合理地進行參數(shù)設(shè)置至今也未有成熟的研究結(jié)論。分層殼單元是一種近年來發(fā)展迅速的適用于鋼筋混凝土板、剪力墻等構(gòu)件精細(xì)化模擬的高效數(shù)值模型，在工程實踐中應(yīng)用廣泛。然而，如何應(yīng)用分層殼模型實現(xiàn)鋼筋混凝土構(gòu)件裂縫寬度的定量預(yù)測，仍鮮有研究。

在上述背景下，本文的主要目標(biāo)是：1) 以彌散裂縫模型和裂縫帶理論為基礎(chǔ)，給出采用通用有限元程序的分層殼單元計算配筋混凝土構(gòu)件裂縫寬度的計算流程；2) 以某承受負(fù)彎矩的鋼-混凝土簡支組合梁為算例，識別影響混凝土裂縫寬度計算結(jié)果的關(guān)鍵參數(shù)，從而對計算過程中的合理參數(shù)設(shè)置提出建議。需要特別說明的是，為便于實際工程的應(yīng)用，本文的討論均不涉及自編程序或基于通用有限元程序的二次開發(fā)，而是討論如何采用已有成熟的通用有限元程序中的彌散裂縫模型和分層殼模型合理地完成配筋混凝土構(gòu)件的裂縫寬度計算。所有算例均采用 MSC.MARC[11]完成，但相關(guān)方法和結(jié)論對于當(dāng)前工程和科研中廣泛采用的其他集成彌散裂縫模型的通用有限元程序(例如：ABAQUS和ANASYS等)均適用。

1 計算理論與流程

1.1 基本假定

本文采用以下三個基本假定：

第一，本文的研究涉及“裂縫寬度”這一非力學(xué)物理量和網(wǎng)格尺寸之間的討論，所有這些討論的前提是：網(wǎng)格密度首先要滿足位移、反力、應(yīng)力、應(yīng)變等力學(xué)物理量的求解精度，不可過于稀疏。

第二，本文僅研究分層殼單元，不直接模擬鋼筋與混凝土之間的粘結(jié)滑移行為，鋼筋與混凝土完全變形協(xié)調(diào)，這也是鋼筋混凝土結(jié)構(gòu)分析中常用的假定。其他建模方式不在本文討論范圍內(nèi)。

第三，本文討論的通用有限元程序需集成彌散裂縫模型框架，對于沒有集成該模型框架的通用有限元程序，無法采用本文建議的方法。

1.2 基于彌散裂縫模型的經(jīng)典裂縫帶理論概述及其局限性

在Bazant和Oh[2]所提出的經(jīng)典裂縫帶理論中，最基本的假定就是：采用斷裂能Gf來描述一根裂縫開裂全過程的力學(xué)行為。斷裂能Gf的定義是：一根裂縫開裂全過程單位面積所耗散的能量，它代表混凝土材料單軸拉應(yīng)力σ與裂縫寬度w關(guān)系曲線的下包面積。之所以引入斷裂能Gf的概念，是因為大量的混凝土直拉試驗表明，同一種混凝土材料無論直拉試件的尺寸如何變化，其測得的σ-w曲線下包面積，也就是斷裂能 Gf，基本是恒定的，這就充分證明了斷裂能Gf是一種混凝土材料性能參數(shù)，與其他諸如立方體抗壓強度 fcu、棱柱體抗壓強度 fc、圓柱體抗壓強度fc′等常用的混凝土材料性能參數(shù)具有同等的位置。筆者團隊[12]曾采用文獻[13—17]中的 17個不同參數(shù)的試件對比了Bazant和Oh[2]、Wittmann等[13]、歐洲模式規(guī)范CEB-FIP MC90[18]建議的斷裂能 Gf公式的計算效果，結(jié)果表明歐洲模式規(guī)范CEB-FIP MC90[18]公式的計算結(jié)果與試驗結(jié)果吻合最好，該公式建議斷裂能Gf主要與混凝土圓柱體抗壓強度 fc′以及最大骨料粒徑 Dmax有關(guān)，具體形式為：

式中： fc′的單位是 N/mm2，若采用中國規(guī)范的混凝土棱柱體抗壓強度 fc時，應(yīng)進行強度轉(zhuǎn)換 fc=0.95fc′；Gf的單位是N/mm；α為系數(shù)，α與最大骨料粒徑 Dmax有關(guān)，Dmax=8 mm 時，α=0.025；Dmax=16 mm時，α=0.03；Dmax=32 mm 時，α=0.058。

圖1所示為裂縫帶理論的一些重要概念。當(dāng)確定了混凝土軸心抗拉強度ft和斷裂能Gf后，只需假定σ -w的曲線形式(通用有限元程序中的彌散裂縫模型常采用最簡單的線性軟化形式，如圖 1(a)所示)，就可以唯一地確定混凝土材料的σ -w關(guān)系。然而，有限元計算是以材料的應(yīng)力-應(yīng)變關(guān)系(σ -ε)為基礎(chǔ)，而σ -w關(guān)系雖然能夠貼切地刻畫混凝土材料的開裂特性，卻無法直接用于有限元計算，因此將σ -w關(guān)系轉(zhuǎn)換為σ -ε關(guān)系則成為非常關(guān)鍵的一步，而這一轉(zhuǎn)換的核心就是將一根集中的裂縫寬度w在一個特定的范圍內(nèi)均勻彌散成應(yīng)變ε，這就是“彌散裂縫”的概念，而這個特定的彌散范圍就是所謂的“裂縫帶”。因此，經(jīng)典裂縫帶理論中的裂縫帶寬hc其實就是裂縫寬度向應(yīng)變彌散的標(biāo)距：

式中，εcr為開裂應(yīng)變，代表一根裂縫寬度在裂縫帶范圍內(nèi)的彌散化。

有了式(2)這一轉(zhuǎn)換關(guān)系，σ -w關(guān)系就可以轉(zhuǎn)換為用于有限元計算的σ -ε關(guān)系，當(dāng)采用如圖 1(b)所示最簡單的受拉線性軟化形式時，Bazant和Oh[2]最終給出了受拉開裂后軟化模量 Ets的計算公式如式(3)所示，在這個公式中，除了裂縫帶寬hc，其他所有參數(shù)都是材料屬性參數(shù)。

式中：ft為混凝土軸心抗拉強度；Ec為混凝土彈性模量。

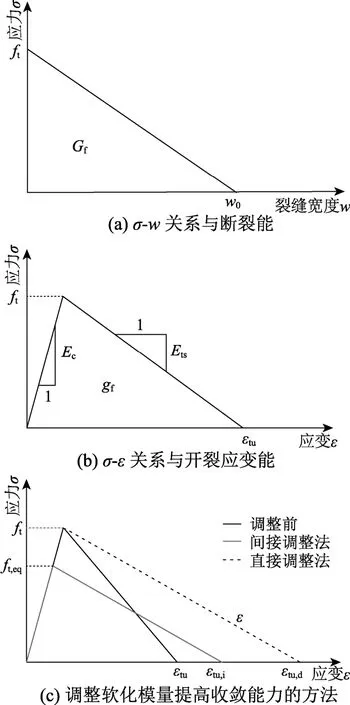
圖1 裂縫帶理論的一些重要概念Fig.1 Some important concepts in the crack band theory

當(dāng)完成有限元分析后，得到的開裂應(yīng)變εcr還需按照式(2)乘以裂縫帶寬 hc才能得到最終需要的裂縫寬度w值。

綜上所述，式(2)和式(3)是裂縫帶理論的兩個核心方程，在這兩個方程中，裂縫帶寬hc無疑是最關(guān)鍵的參數(shù)。因此，采用裂縫帶理論進行混凝土開裂有限元分析的核心就是要選取合適的裂縫帶寬hc，經(jīng)典的裂縫帶理論認(rèn)為裂縫帶寬 hc應(yīng)選為單元特征尺寸lele(垂直于裂縫方向單元尺寸的投影)，也就是當(dāng)采用不同的單元網(wǎng)格尺寸分析同一個問題時，如果采用相同的參數(shù)設(shè)置，那么計算結(jié)果就與網(wǎng)格相關(guān)，如果要使計算結(jié)果一致，那么參數(shù)取值就要與網(wǎng)格相關(guān)。

網(wǎng)格相關(guān)是經(jīng)典裂縫帶理論最重要的結(jié)論之一，其背后的力學(xué)本質(zhì)是混凝土開裂作為一種軟化行為具有顯著的局部化(Localization)特點。為了更清晰地闡明這一機理，本文采用通用有限元程序MSC.MARC[11]中的彌散裂縫模型完成了一個算例。圖2所示為算例的基本信息及計算結(jié)果。

該算例為跨中承受豎向集中荷載的一根簡支無筋素混凝土梁，該梁的基本尺寸如圖2(a)所示，采用分層殼單元模擬該梁的全過程開裂行為。分別建立三個數(shù)值模型：模型A采用100 mm的單元網(wǎng)格進行計算，計算過程中的裂縫帶寬hc也取為100 mm，與單元尺寸相同；模型B在模型A的基礎(chǔ)上加密1倍網(wǎng)格，采用50 mm的單元網(wǎng)格進行計算，但計算過程中的裂縫帶寬hc仍保持不變，取為100 mm；模型C同樣在模型A的基礎(chǔ)上加密一倍網(wǎng)格，采用50 mm的單元網(wǎng)格進行計算，但計算過程中的裂縫帶寬hc也隨之變?yōu)榕c單元網(wǎng)格50 mm一致。表1詳細(xì)列出了這三個模型的具體參數(shù)取值，混凝土材料受壓性能設(shè)為彈性，只考慮其受拉開裂的行為。采用位移控制對模型進行加載，分為均勻的400個加載子步逐步對跨中施加豎向位移至2 mm。采用殘余力的收斂準(zhǔn)則，收斂誤差限設(shè)為0.02。

圖2 跨中單點加載素混凝土梁算例Fig.2 Example of plain concrete beam subjected to mid-span point load

表1 素混凝土梁數(shù)值算例參數(shù)Table 1 Parameters of numerical example of plain concrete beam

圖2還給出了三個模型的計算結(jié)果對比，包括：跨中梁底最大裂縫寬度w隨跨中豎向位移δ 的變化曲線(如圖2(b)所示)以及跨中荷載P隨跨中梁底最大裂縫寬度w的變化曲線(如圖2(c)所示)，在計算單元裂縫寬度w的過程中，提取的開裂應(yīng)變?yōu)閱卧?個積分點開裂應(yīng)變值的平均值。這些計算結(jié)果可從以下兩個方面進行討論：

1) 對比模型 A和模型 B，兩者采用的單元網(wǎng)格尺寸不同，而計算參數(shù)hc取值相同，所得的計算結(jié)果差距很大，由此可證明：當(dāng)采用不同的單元網(wǎng)格尺寸分析同一個問題，如果采用相同的參數(shù)設(shè)置，那么計算結(jié)果就與網(wǎng)格相關(guān)。

2) 對比模型 A和模型 C，兩者采用的單元網(wǎng)格尺寸不同，而計算參數(shù)hc也隨著網(wǎng)格尺寸的變化按照經(jīng)典裂縫帶理論進行調(diào)整，所得的計算結(jié)果幾乎相同，由此又可證明：當(dāng)采用不同的單元網(wǎng)格尺寸分析同一個問題，如果要使計算結(jié)果一致，那么參數(shù)取值就要與網(wǎng)格相關(guān)。

以上兩組對比充分驗證了經(jīng)典裂縫帶理論的網(wǎng)格相關(guān)性，而這種相關(guān)性可以進一步從構(gòu)件的破壞模式進行解釋。對于一根素混凝土梁，當(dāng)跨中梁底出現(xiàn)第一根裂縫后，承載力就會急劇下降，其他位置就不會再出現(xiàn)新的裂縫，如圖2(d)所示三個模型計算得到的變形和開裂應(yīng)變云圖(跨中撓度達(dá)到2 mm時)就很好地模擬了這種破壞特征。而進一步仔細(xì)觀察各單元的應(yīng)力-應(yīng)變變化過程，當(dāng)跨中截面單元率先達(dá)到混凝土軸心抗拉強度ft后開裂進入軟化段本構(gòu)時，其余截面單元則隨著構(gòu)件承載力的下降進行彈性卸載而無法進入開裂，因此無論單元如何劃分，只有跨中截面的一列單元會進入開裂，一根裂縫總是在一個單元的范圍內(nèi)彌散，所以裂縫帶寬hc自然應(yīng)取為一個單元的尺寸lele。此外，圖2(d)云圖中的開裂應(yīng)變數(shù)值也可印證這一規(guī)律，模型B和模型C的單元網(wǎng)格尺寸相比模型A縮小了一倍，而他們的開裂應(yīng)變數(shù)值也相應(yīng)放大了大約1倍，因為裂縫彌散成應(yīng)變的標(biāo)距縮小了，自然應(yīng)變就放大了，可見裂縫彌散成應(yīng)變的標(biāo)距，也就是裂縫帶寬hc，應(yīng)該就是單元網(wǎng)格尺寸了。

值得關(guān)注的是，與上面這個算例類似，Bazant和 Oh[2]在論文中討論的都是不配筋的素混凝土構(gòu)件，用于模型驗證的試驗都是不配筋素混凝土的缺口試驗，這些構(gòu)件最大的特點是一旦在最薄弱的地方出現(xiàn)一條裂縫后，就不會在其他地方出現(xiàn)新的裂縫，自然具有顯著的局部化特點。然而，實際工程結(jié)構(gòu)中絕大部分都采用配筋混凝土構(gòu)件，由于配筋的存在，混凝土的裂縫以某一個間距均勻地分布在構(gòu)件中，這種裂縫的分布模式與素混凝土構(gòu)件的集中分布模式截然不同。退一步講，實際工程里即使采用素混凝土或配筋很少的混凝土構(gòu)件，一旦達(dá)到混凝土軸心抗拉強度開裂后，就馬上發(fā)生脆性破壞喪失承載力(如圖 2(c)所示)，因此這種構(gòu)件在實際工程中根本不允許出現(xiàn)裂縫，而此時再去研究如何計算開裂后的裂縫寬度則顯得毫無意義。因此，針對素混凝土結(jié)構(gòu)構(gòu)件的經(jīng)典裂縫帶理論離結(jié)構(gòu)工程實踐具有一定的距離，只有將裂縫帶理論根據(jù)配筋混凝土構(gòu)件的力學(xué)特點進行改造和拓展，才能真正解決結(jié)構(gòu)工程的問題，這也是接下來本文要進一步討論的內(nèi)容。

1.3 裂縫帶理論在配筋混凝土構(gòu)件中的表達(dá)形式

在配筋混凝土構(gòu)件中，由于鋼筋和混凝土之間的粘結(jié)作用，混凝土的裂縫以某一特定的間距分布出現(xiàn)，因此，在一個有限元網(wǎng)格 lele范圍內(nèi)有可能出現(xiàn)多根裂縫，這是與素混凝土構(gòu)件在開裂行為上最顯著的區(qū)別。基于這樣的認(rèn)識，可以將一個單元內(nèi)的開裂應(yīng)變看作這一個單元內(nèi)所有裂縫寬度總和的彌散化，因此開裂應(yīng)變εcr與一根裂縫的寬度w之間滿足以下關(guān)系式：

式中，n為一個單元內(nèi)的平均裂縫數(shù)量。

Bazant和Oh[2]定義開裂應(yīng)變能gf如下：

圖3所示為開裂應(yīng)變和開裂應(yīng)變能的定義。裂縫帶模型認(rèn)為，混凝土開裂后，其彈性拉應(yīng)變εte隨應(yīng)力的降低而逐漸降低，其在開裂前積累的彈性應(yīng)變能在開裂后是緩慢釋放的，在受拉軟化曲線上任意一點的應(yīng)變ε，均可分解為彈性應(yīng)變εte和開裂應(yīng)變εcr，如圖3(a)所示，式(5)所定義的開裂應(yīng)變能gf表示的就是圖3(a)中曲線下部涂色部分的面積。這里需要補充的是，一些通用有限元程序中的彌散裂縫模型與這一定義略有區(qū)別，譬如，MSC.MARC[11]認(rèn)為混凝土開裂后，其彈性應(yīng)變能瞬間釋放，在受拉軟化曲線上任意一點的應(yīng)變ε就是開裂應(yīng)變，則開裂應(yīng)變能gf表示的面積比Bazant和Oh[2]定義的面積大，如圖3(b)所示，這兩個觀點雖然對混凝土開裂機理的解釋是不同的，但由于實際工程重點關(guān)注正常使用極限狀態(tài)下(荷載水平大約為極限荷載的50%)裂縫穩(wěn)定形成后的裂縫寬度值，此時這一差別就顯得無關(guān)緊要，因為在混凝土從受拉到完全開裂(應(yīng)力降為 0)的過程中發(fā)生的總開裂應(yīng)變能 gf均指的是受拉應(yīng)力-應(yīng)變關(guān)系曲線的下部面積(如圖1(b)所示)，且完全開裂點的開裂應(yīng)變εcr均與總應(yīng)變ε 相等。因此，裂縫開裂全過程的總開裂應(yīng)變能 gf可寫為：

式中，εtu為完全開裂點的總應(yīng)變，如圖3所示。

根據(jù)斷裂能的定義，一根裂縫開裂全過程的斷裂能Gf為：

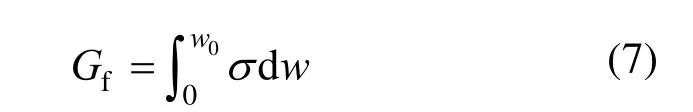
式中，w0的含義為完全開裂(拉應(yīng)力為 0)時的裂縫寬度，如圖1(a)所示。

圖3 開裂應(yīng)變和開裂應(yīng)變能的定義Fig.3 Definitions of crack strain and crack strain energy

根據(jù)式(4)、式(6)和式(7)，可以推出裂縫開裂全過程gf與Gf的關(guān)系為：

根據(jù)平均裂縫間距l(xiāng)m的含義，即可得到一個單元內(nèi)的平均裂縫數(shù)量n如下：

將式(9)代入式(8)，gf與Gf之間的關(guān)系可進一步寫為式(10)，可以發(fā)現(xiàn)式(10)與單元網(wǎng)格尺寸lele無關(guān)。

由于 gf代表的為受拉應(yīng)力-應(yīng)變曲線的下部面積，若同樣采用如圖1(b)所示最簡單的受拉線性軟化形式時，gf可具體寫為：

將式(11)代入式(10)，即可得到軟化模量 Ets的表達(dá)式如下：

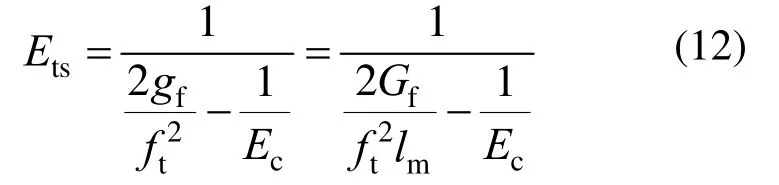
從式(12)可以得到一個非常重要的結(jié)論，那就是對于配筋混凝土構(gòu)件，基于裂縫帶理論推導(dǎo)得到的混凝土單軸應(yīng)力-應(yīng)變關(guān)系與單元網(wǎng)格尺寸無關(guān)，與素混凝土的結(jié)論截然相反。這一結(jié)論意味著當(dāng)采用有限元方法進行配筋混凝土構(gòu)件的裂縫寬度分析時，不必考慮單元網(wǎng)格劃分對計算結(jié)果的影響，這給配筋混凝土構(gòu)件的裂縫寬度分析帶來了極大的便利，因為在實際結(jié)構(gòu)的分析中，網(wǎng)格劃分的選取往往受制于構(gòu)件布置、計算代價等其他諸多因素，如果計算結(jié)果與網(wǎng)格無關(guān)，那么網(wǎng)格劃分在具體操作過程中就會比較自由。

式(12)還表明，當(dāng)混凝土材料一定時，斷裂能Gf、混凝土開裂應(yīng)力ft、混凝土彈性模量Ec都是確定的，則平均裂縫間距l(xiāng)m是影響混凝土受拉本構(gòu)關(guān)系的最關(guān)鍵因素。裂縫越密，則軟化模量 Ets就越小，曲線的下降段就越緩。這一規(guī)律同樣可以從裂縫帶理論的基本假定加以解釋，裂縫越密集意味著單位長度內(nèi)的裂縫數(shù)量越多，而單個裂縫開裂所需的斷裂能Gf是一定的，越多的裂縫數(shù)量意味著構(gòu)件受拉過程中耗散的能量越多，因此，構(gòu)件因開裂導(dǎo)致的損傷退化發(fā)展也就越遲緩，表現(xiàn)在應(yīng)力-應(yīng)變關(guān)系上就是曲線下降段越緩。

最后，當(dāng)完成非線性有限元分析后，可根據(jù)得到的開裂應(yīng)變εcr按式(13)算得裂縫寬度值。同樣的，這一公式也與網(wǎng)格尺寸無關(guān)。

分別對比式(12)與式(3)、式(13)與式(2)，對于配筋混凝土結(jié)構(gòu)，裂縫帶理論中的核心參數(shù)——裂縫帶寬hc應(yīng)取為平均裂縫間距l(xiāng)m，而非單元特征尺寸 lele，這從裂縫帶的基本概念入手也非常容易解釋，裂縫帶表示一根集中的裂縫寬度均勻彌散成應(yīng)變的范圍，對于按一定間距l(xiāng)m分布的一系列裂縫，每一根裂縫恰好向兩側(cè)各 0.5lm范圍內(nèi)彌散才能恰好使所有裂縫彌散到開裂單元的所有范圍內(nèi)。

以上討論均在理論層面，但在實踐層面，混凝土開裂分析作為強非線性分析，常常會遇到難以回避的收斂性問題。軟化模量 Ets對程序的收斂性具有十分關(guān)鍵的影響，許多時候，按照式(12)計算出來的軟化模量Ets值較大(尤其是配筋率不太高的情況下，平均裂縫間距較大)，此時雖然理論上很完善，但輸入到程序中卻難以收斂，無法得到計算結(jié)果，那么這種理論上的完善就失去了意義。應(yīng)對此問題時最常見的做法就是人為地調(diào)小軟化模量 Ets值，使程序收斂，本文將該方法簡稱為“直接調(diào)整法”，如圖1(c)所示，但這樣的做法改變了材料的斷裂能，從根本上違背了“斷裂能是表征裂縫力學(xué)行為的本質(zhì)參數(shù)”這一基本結(jié)論，其可能導(dǎo)致的誤差將在后面的算例中做進一步的討論。而另一種可行的做法是仍然堅持“采用斷裂能來描述一根裂縫開裂全過程的力學(xué)行為”這一最基本的假定，在保證應(yīng)力-應(yīng)變關(guān)系曲線下包面積不變(也就是開裂應(yīng)變能 gf不變)的情況下，通過人為調(diào)小開裂應(yīng)力ft至ft,eq，來間接地調(diào)小軟化模量，使程序便于收斂，本文將該方法簡稱為“間接調(diào)整法”，如圖1(c)所示，這一做法的效果也將在后面的算例中進行討論。

1.4 計算流程總結(jié)

在上述討論的基礎(chǔ)上，本文總結(jié)了采用通用有限元程序的彌散裂縫模型和分層殼單元計算裂縫寬度的流程，如圖4所示。在這一計算流程中，平均裂縫間距l(xiāng)m占據(jù)了至關(guān)重要的位置，它架起了連接“應(yīng)變”與“裂縫寬度”的橋梁，從而實現(xiàn)了有限元計算的“開裂應(yīng)變”轉(zhuǎn)換為“裂縫寬度”這一最終目標(biāo)。關(guān)于該計算流程的具體說明如下：

步驟1：根據(jù)混凝土棱柱體抗壓強度fc和最大骨料粒徑Dmax，經(jīng)過相應(yīng)的強度換算采用式(1)計算斷裂能Gf；

步驟 2：采用理論或經(jīng)驗公式計算平均裂縫間距l(xiāng)m；

步驟3：根據(jù)式(10)通過lm將斷裂能Gf轉(zhuǎn)換為開裂應(yīng)變能gf，也就是應(yīng)力-應(yīng)變曲線的下包面積；

步驟4：由應(yīng)力-應(yīng)變曲線的下包面積gf，根據(jù)混凝土彈性模量Ec和混凝土軸心抗拉強度ft，采用式(12)算得受拉軟化模量Ets，輸入有限元程序進行非線性有限元分析；

步驟5：若程序不收斂，則將ft折減為ft,eq，重新按步驟4計算，若程序收斂，則提取有限元程序算得的開裂應(yīng)變εcr；

步驟6：根據(jù)式(13)通過lm將開裂應(yīng)變εcr轉(zhuǎn)換為裂縫寬度w。

在有限元的理論體系里只存在“應(yīng)變”的概念，但要完整地描述開裂行為必須要有“平均裂縫間距”和“裂縫寬度”兩個物理量，因此，單純依靠有限元方法，裂縫是不可解的，這就是有限元方法在處理非連續(xù)介質(zhì)問題時的固有缺陷。這也從根本上解釋了為什么在上述計算流程中，平均裂縫間距 lm需要游離于有限元裂縫分析過程之外預(yù)先單獨計算確定，而無法在有限元裂縫分析過程之中自動解得。同時，這也表明平均裂縫間距在開裂應(yīng)變與裂縫寬度之間的重要作用，確定平均裂縫間距的取值成為裂縫計算不可或缺的條件。

圖4 采用通用有限元程序計算裂縫寬度的建議流程Fig.4 Proposed procedure for calculating the crack width using general-purpose finite element packages

目前，確定平均裂縫間距l(xiāng)m主要依賴于半經(jīng)驗半理論公式，通過試驗數(shù)據(jù)回歸是確定平均裂縫間距的最常用方法，此種方法在平均裂縫間距求解的機理上存在一定缺陷，更通用的計算方法仍有待進一步研究。

2 算例討論

2.1 算例參數(shù)和模擬結(jié)果

為全面驗證并討論上述計算理論和流程，選取一由聶建國等[19]完成的承受負(fù)彎矩作用的簡支組合梁靜力加載試驗進行有限元分析，分析的重點是定量預(yù)測混凝土板裂縫寬度的全過程發(fā)展。

圖5所示為算例的基本信息及網(wǎng)格的劃分。算例的具體參數(shù)和加載模式如圖5(a)所示。基于通用有限元程序 MSC.MARC[11]中的彌散裂縫模型，采用梁-殼混合模型進行分析，鋼筋混凝土板采用分層殼單元進行模擬(混凝土分為 5層)，鋼梁采用纖維梁單元進行模擬(鋼梁上翼緣、腹板、下翼緣的纖維劃分?jǐn)?shù)分別為16、20、16)。該梁-殼混合模型的單元類型、材料本構(gòu)等建模信息詳見文獻[20—22]。分析采用位移收斂準(zhǔn)則，誤差限設(shè)為0.01。

平均裂縫間距l(xiāng)m是計算中的關(guān)鍵參數(shù)，由于承受負(fù)彎矩的組合梁其混凝土板近似處于軸心受拉狀態(tài)，因此這里采用文獻[23]建議的軸心受拉鋼筋混凝土構(gòu)件的平均裂縫間距l(xiāng)m計算公式，具體如下：

式中：c為保護層厚度；dr為鋼筋直徑；ρr為配筋率。

圖5 承受負(fù)彎矩的簡支組合梁[19]Fig.5 Simply supported composite beam under hogging moment[19]

2.2 結(jié)果的網(wǎng)格依賴性

網(wǎng)格無關(guān)性是裂縫帶理論推廣到配筋混凝土構(gòu)件時的重要特性，為驗證這一結(jié)論，這里分別采用如圖5(b)所示的4種不同的單元劃分進行模擬，從模型A到模型D，單元網(wǎng)格由密到疏。

網(wǎng)格尺寸對模擬結(jié)果的影響如圖 6所示。圖6(a)給出了采用不同網(wǎng)格尺寸計算得到的跨中彎矩-跨中撓度曲線及其與試驗結(jié)果的對比。不同單元網(wǎng)格的模型給出幾乎完全一致的結(jié)果，說明結(jié)果確實與網(wǎng)格無關(guān)。所有的計算結(jié)果都與試驗結(jié)果吻合良好，也驗證了模型的準(zhǔn)確性。此外，文獻[20—22]對本算例采用的梁-殼混合模型開展了大量的試驗驗證，充分驗證了該模型的可靠性。圖 6(b)給出了跨中彎矩-跨中板分層殼單元頂層裂縫寬度曲線，網(wǎng)格尺寸對計算結(jié)果也幾乎沒有影響。此外，當(dāng)混凝土板頂纖維達(dá)到開裂應(yīng)力 ft后，計算曲線的裂縫寬度值發(fā)生突變，這也很好地印證了前述MSC.MARC[11]采用的彈性應(yīng)變能集中釋放的假定。

圖6 網(wǎng)格尺寸對模擬結(jié)果的影響Fig.6 Influence of mesh size on the simulation results

為進一步驗證模型的網(wǎng)格無關(guān)性，圖7對比了兩個荷載水平下不同網(wǎng)格尺寸模型給出的混凝土板分層殼單元頂層開裂區(qū)范圍，同樣可以清楚地看到，不同的網(wǎng)格劃分計算出的混凝土板開裂區(qū)范圍也非常接近。以上從各個角度充分證明了單元網(wǎng)格的無關(guān)性，后續(xù)的分析均采用模型D的網(wǎng)格劃分，進一步研究軟化模量的調(diào)整方法和平均裂縫間距對裂縫寬度計算結(jié)果的影響。

圖7 不同網(wǎng)格尺寸混凝土板開裂區(qū)范圍計算結(jié)果對比Fig.7 Comparison of calculation results of cracking zone range of RC slab among different mesh sizes

2.3 軟化模量相關(guān)收斂困難的應(yīng)對策略

為應(yīng)對基于裂縫帶理論計算得到的軟化模量Ets過大而導(dǎo)致的收斂困難，前述從理論層面討論了兩種應(yīng)對策略：一種是直接人為調(diào)小軟化模量 Ets值，即“直接調(diào)整法”；另一種是基于斷裂能等效通過調(diào)小開裂應(yīng)力ft來間接調(diào)小軟化模量Ets值，即“間接調(diào)整法”。以下通過對本算例進行參數(shù)分析，進一步討論這兩種調(diào)整法的實際計算效果，以期對理論部分討論的結(jié)論進行驗證。

首先討論“直接調(diào)整法”。軟化模量Ets調(diào)整為裂縫帶理論計算值的0.75倍和0.5倍，同時保持其他所有參數(shù)不變。采用“直接調(diào)整法”處理的計算結(jié)果如圖8所示。圖8(a)給出了跨中板分層殼單元頂層裂縫寬度隨荷載的發(fā)展曲線對比，可見三根曲線有顯著的差異。調(diào)小軟化模量對開裂點以及剛開裂之后的一小段裂縫發(fā)展的計算結(jié)果沒有影響，但隨著荷載水平不斷提高，裂縫不斷發(fā)展，裂縫寬度的預(yù)測誤差逐步增大，直到荷載水平大約超過極限承載力的50%后，裂縫寬度的預(yù)測誤差才逐漸減小直至所有曲線又回到相同的結(jié)果。因此，“直接調(diào)整法”會導(dǎo)致正常使用荷載水平下顯著的裂縫寬度預(yù)測誤差，盡管如此，從圖8(b)可以看到這一調(diào)整對宏觀曲線的影響較小。

圖8 “直接調(diào)整法”應(yīng)對軟化模量過大導(dǎo)致收斂困難的效果Fig.8 Effect of direct adjustment method for overcoming the convergence difficulty due to large softening modulus

下面進一步討論“間接調(diào)整法”，也是本文推薦的方法。因為軟化模量的大小直接決定收斂的困難程度，為了使兩種方法具有可比性，這里在保證開裂應(yīng)變能不變的情況下通過調(diào)整開裂應(yīng)力ft同樣使軟化模量Ets變?yōu)榱芽p帶理論計算值的0.75倍和0.5倍，即近似達(dá)到同樣的收斂難易度。由式(11)可知，調(diào)整后的等效開裂應(yīng)力 ft,eq與真實開裂應(yīng)力ft的比值γ 按式(15)計算：

式中，β為調(diào)整后的軟化模量與裂縫帶理論計算得到的軟化模量的比值，對本算例，當(dāng)β 取為0.75和0.5時，γ 分別為0.878和0.726。

采用“間接調(diào)整法”處理的計算結(jié)果如圖 9所示。圖9(a)給出了采用“間接調(diào)整法”后跨中板分層殼單元頂層裂縫寬度隨荷載的發(fā)展曲線對比，可見其誤差情況與“直接調(diào)整法”完全相反，由于改變了開裂應(yīng)力，開裂荷載以及剛開裂后的一小段裂縫發(fā)展有一定的誤差，但很快隨著荷載水平逐步提高(大約荷載水平提高到極限荷載的 20%之后)，三個模型幾乎給出相同的裂縫寬度預(yù)測結(jié)果。因此，“間接調(diào)整法”在達(dá)到與“直接調(diào)整法”同樣的軟化模量折減效果的同時，也很好地保證了正常使用荷載水平下裂縫寬度的預(yù)測精度，同時由圖9(b)還可以看到，“間接調(diào)整法”除了略微改變了開裂點附近的宏觀曲線外，對整體宏觀曲線的影響也很小，可見“間接調(diào)整法”是一種非常理想的應(yīng)對軟化模量過大導(dǎo)致收斂困難的策略。

圖9 “間接調(diào)整法”應(yīng)對軟化模量過大導(dǎo)致收斂困難的效果Fig.9 Effect of indirect adjustment method for overcoming the convergence difficulty due to large softening modulus

為了更直觀地展現(xiàn)兩種調(diào)整法的計算效果，圖10(a)和圖 10(b)分別給出了兩種調(diào)整法在不同荷載水平(定義為實際荷載與極限荷載的比值)下裂縫寬度值的預(yù)測誤差，圖10中w0為采用裂縫帶理論得到的裂縫寬度值，是衡量誤差的基準(zhǔn)。從圖 10中可以清楚地看到，“直接調(diào)整法”產(chǎn)生誤差的主要荷載水平范圍為20%~50%，“間接調(diào)整法”產(chǎn)生誤差的主要荷載水平范圍為20%以下，而實際混凝土結(jié)構(gòu)構(gòu)件正常使用階段裂縫寬度驗算最關(guān)心的荷載水平范圍恰好落在 20%~50%，因此對于面向?qū)嶋H工程結(jié)構(gòu)應(yīng)用的裂縫寬度預(yù)測，應(yīng)選用“間接調(diào)整法”。

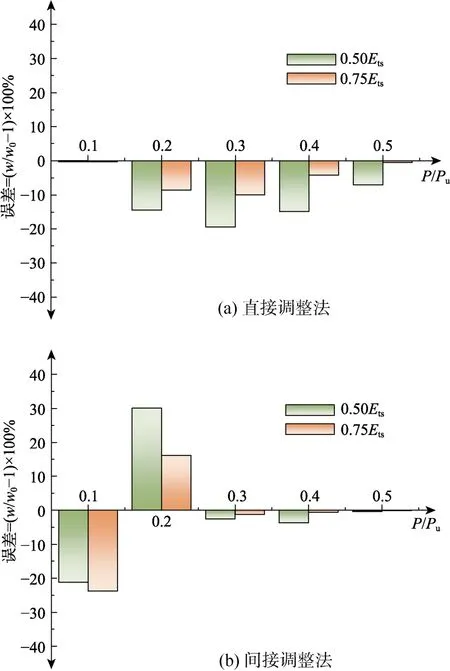
圖10 不同荷載水平下裂縫寬度的預(yù)測誤差Fig.10 Crack width prediction errors under different load levels

實際上，無論采用哪種調(diào)整法，在材料本構(gòu)層面產(chǎn)生的誤差主要都集中在材料完全開裂點(即拉應(yīng)變達(dá)到圖1(c)中的εtu)之前，從圖8(a)和圖9(a)中也可清楚地看到，當(dāng)混凝土材料的拉應(yīng)變達(dá)到完全開裂點εtu之后，裂縫寬度的預(yù)測誤差就開始顯著減小，而主要的誤差都集中在材料達(dá)到完全開裂點εtu之前，因此要減小調(diào)整軟化模量造成的誤差，就需要盡可能提前εtu，使得材料完全開裂點盡可能避開混凝土結(jié)構(gòu)構(gòu)件正常使用狀態(tài)的荷載水平，而圖1(c)清楚地表明，要達(dá)到同樣的軟化模量折減程度，“間接調(diào)整法”求得的完全開裂點εtu相比“直接調(diào)整法”求得的完全開裂點有顯著的提前，這也從基本原理上進一步解釋了為什么應(yīng)當(dāng)選用“間接調(diào)整法”。

2.4 平均裂縫間距的影響

如前所述，平均裂縫間距l(xiāng)m是整個計算流程中的關(guān)鍵參數(shù)，它架起了連接“應(yīng)變”與“裂縫寬度”的橋梁，因此作為討論的最后一部分，本節(jié)將重點研究平均裂縫間距對計算結(jié)果的影響。將平均裂縫間距分別變化為式(14)計算值的0.5倍、0.75倍、1.25倍和1.5倍，其他參數(shù)均保持不變，代入圖4所示的流程進行計算。圖11(a)對比了跨中板分層殼單元頂層裂縫寬度隨荷載的發(fā)展曲線，清晰地展示了平均裂縫間距對裂縫寬度計算結(jié)果的決定性作用，采用不同的平均裂縫間距得到的裂縫寬度結(jié)果差異很大，因此要得到準(zhǔn)確可靠的裂縫寬度值，選取準(zhǔn)確可靠的平均裂縫間距至關(guān)重要。而圖11(b)表明，平均裂縫間距的改變對宏觀曲線的影響仍然較小，可以忽略。

圖11 平均裂縫間距對模擬結(jié)果的影響Fig.11 Influence of the average crack spacing on the simulation results

3 關(guān)于網(wǎng)格無關(guān)性的其他佐證

“網(wǎng)格無關(guān)性”是本文研究的重要結(jié)論，為了進一步說明該結(jié)論的可靠性，以下給出了一些其他佐證材料供讀者參考。

1) 代爾夫特科技大學(xué)(Delft University of Technology)的 Rots在他的博士論文[24]中對這個問題開展了一系列算例研究，發(fā)現(xiàn)當(dāng)直接模擬鋼筋與混凝土的粘結(jié)滑移效應(yīng)時，裂縫計算結(jié)果和網(wǎng)格相關(guān)，而如果使鋼筋與混凝土直接變形協(xié)調(diào)，裂縫寬度則與平均裂縫間距相關(guān)，他還引用了當(dāng)年國際上很有代表性的 Collins等[25]完成的鋼筋混凝土平板試驗來證明這個結(jié)論。

2) de Borst曾于2002年在《Engineering Fracture Mechanics》中發(fā)表綜述論文[26]，也發(fā)現(xiàn)了對于鋼筋混凝土構(gòu)件，在計算裂縫帶寬時，需要考慮平均裂縫間距的影響。

3) 這里再補充一個算例來說明網(wǎng)格無關(guān)性結(jié)論，該算例為一單純的鋼筋混凝土簡支板，如圖12所示。計算結(jié)果如圖 13所示，通過對比不同網(wǎng)格尺寸對應(yīng)的跨中彎矩-跨中撓度曲線以及跨中彎矩-跨中板分層殼單元底層裂縫寬度曲線，同樣可以得到網(wǎng)格無關(guān)性的結(jié)論。

圖12 鋼筋混凝土簡支板Fig.12 Simply supported reinforced concrete slab

4) 作為分層殼單元向一維化的退化，纖維梁單元近年來也廣泛應(yīng)用于結(jié)構(gòu)分析，這種建模方式和分層殼單元一樣不直接模擬鋼筋與混凝土層之間的粘結(jié)滑移，筆者團隊通過算例研究也證明了采用纖維梁模型模擬鋼筋混凝土構(gòu)件裂縫寬度同樣與網(wǎng)格無關(guān)，詳見文獻[27]。

圖13 網(wǎng)格尺寸對模擬結(jié)果的影響Fig.13 Influence of mesh size on the simulation results

4 結(jié)論

本文討論了采用通用有限元程序的彌散裂縫模型和分層殼單元計算鋼筋混凝土裂縫寬度的理論基礎(chǔ)與方法。本文首先簡要回顧了基于彌散裂縫模型的經(jīng)典裂縫帶理論，并結(jié)合某無筋素混凝土梁的有限元算例討論了該理論的局限性。在此基礎(chǔ)上，從配筋混凝土結(jié)構(gòu)構(gòu)件的裂縫發(fā)展特點出發(fā)，推導(dǎo)了裂縫帶理論在配筋混凝土構(gòu)件中的表達(dá)形式，討論了數(shù)值收斂問題的應(yīng)對策略，并給出了計算流程。最后，以某承受負(fù)彎矩的簡支組合梁混凝土板開裂分析為例，全面驗證了本文理論討論部分的關(guān)鍵結(jié)論。總結(jié)本文研究，可得如下重要結(jié)論：

(1) 對于無筋素混凝土結(jié)構(gòu)構(gòu)件，單裂縫軟化的局部化效應(yīng)導(dǎo)致有限元計算結(jié)果與網(wǎng)格密切相關(guān)，裂縫帶理論中的裂縫帶寬應(yīng)取為單元特征尺寸。

(2) 對于配筋混凝土結(jié)構(gòu)構(gòu)件，多根裂縫按照平均裂縫間距均勻分布，有限元計算結(jié)果與網(wǎng)格無關(guān)，裂縫帶理論中的裂縫帶寬應(yīng)取為平均裂縫間距。

(3) 平均裂縫間距將有限元分析中的“應(yīng)變”概念和工程設(shè)計中的“裂縫寬度”概念緊密聯(lián)系起來，是本文建議計算流程中最重要的參數(shù)，對計算結(jié)果具有決定性的影響。

(4) 當(dāng)遇到軟化模量過大而導(dǎo)致的數(shù)值收斂問題時，建議在保持?jǐn)嗔涯艿刃У那疤嵯峦瑫r調(diào)整混凝土軸心抗拉強度和軟化模量值。

在本文的討論中，“平均裂縫間距”始終是最核心的關(guān)鍵詞，因此，更通用化的平均裂縫間距計算方法非常值得進一步研究，作為初步的探索，筆者所在團隊嘗試將斷裂能判據(jù)引入有限元方法求解平均裂縫間距，相關(guān)討論詳見文獻[28]。此外，“受拉剛化效應(yīng)”本文未討論，因為要考慮該效應(yīng)不可避免需對通用有限元程序進行二次開發(fā)，故不在本文的討論范圍內(nèi)，筆者在文獻[12]和文獻[27]中對此問題有專門的討論，讀者可查閱。