從課改的視角淺談數學創新性思維的培養

溫瑜文

新大綱、課改反映出的新理念，把數學教學帶入了一個全新的境界。課改體現的素質教育思想，反映在數學教育中即為通過數學教學，讓所有的學生學會對自己有用的數學。以學生終身發展為本，是課改編寫的基點;以學生主動探究、親自體驗為特征，是課改內容體現的重點;知識來源于生活、應用于生活是課改的熱點;讓所有學生的個性得到尊重、理解和健全，是課改創新教育的靈魂。我們完全有必要重新審視數學學科的教學目的，把創新意識的培養作為教學的重要任務;教學實際，把傳授知識培養學生的創新精神與新思維有機地結合起來。本文就“從課改的視角談數學創新性思維的培養”談幾點做法和體會。

一、領會新大綱新的教育理念，培養學生的創新意識

新大綱教學建議指出：“數學教學是數學活動的教學，是師生之間、學生之間交往互動與共同發展的過程。學生是數學活動的主人，教師是學生數學活動的組織者、引導者與合作者。”這也就要求教師要從傳統的應試教育的圈子跳出來，具備創新教學理念，傳統的教育觀的基本特點是以教師為中心的單向傳授，學生的學習方式是接受式學習，被動式反應。而新的教育要在教學過程中要體現“學生為主體，教師為主導，訓練為主線，思維為核心”的教學思想;同時體現了學生身心發展特點，尊重學生的人格及創造精神，把教學的重心和立足轉移到引導學生主動積極的“學”上來，引導學生想學、會學、善學。

二、發掘課改的創新思維因素，培養學生創新性思維。

（一）思想方法要注意“點化”

1.數學思想是對數學事實、概念、理論和方法的本質認識。數學方法是實施有關數學思想的技術手段，它們是數學知識的核心，通常分三個層次，即數學思想（如函數思想、分類思想、數形結合思想等）、邏輯方法（如歸納法、演繹法、類比法等）、具體的數學方法（如配方法、換元法等）。因此，在教學中應重在點化，高度重視數學思想的挖掘和滲透，讓學生領會其價值，滋生應用意識，培養創新思維。

2.新課程內容標準分“數與代數”“空間與圖形”“統計與概率”“實踐與綜合應用”四個領域。其基本思路是以反映未來社會公民所必須的數學思想方法為主線選擇和安排內容，以與學生年齡特征相適應的大眾化、生活化的方式呈現數學內容，使學生在活動中、在現實生活中學習數學、發展數學，更好地體會數學在現實生活中的應用價值。因此，教師完全能夠通過挖掘教材，高效地駕馭教材，把與時代發展相適應的新知識、新問題引入課堂，與教材內容有機結合，引導學生再去主動探究。讓學生掌握更多的方法，了解更多的知識，培養學生的創新精神。

（二）例題講解要注意“變化”

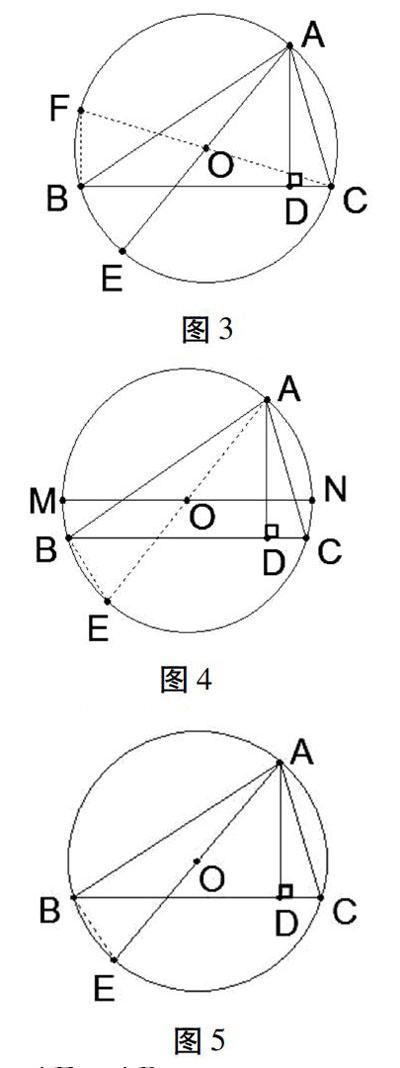
教材的例題選擇是突出教材重點，選擇具有典型性的題目，反映“教學大綱”中最主要、最基本的要求。在對例題進行分析和解答后，應注意發揮例題的示范功能，力求在例題的基礎上進一步變化，使平日所學的零散知識系統化，形成良好的知識結構。可遵循：溫故原則、解惑原則、發現原則、探究原則。以教材初中《幾何》第三冊79頁例題2為例，我就自擬一題多變的問題談一些淺見。教材的例題是：如圖1，AD是△ABC的高，AE是△ABC的外接圓直徑，求證：AB·AC=AE·AD

1.仿造變化。模仿課本中的例題和習題，變化某些數據，或把證明題變為計算題（或反之）等手段，將原題作適當變化而編成新題目，這類題解法與原形的題的解法基本一致。

例1：如圖1，AD是△ABC的高，AE是△ABC的外接圓的直徑，若圓的半徑為5，AD的長是4，求AB·AC的值。

2.反向變式。改變原命題的敘述方式，把原命題的“條件”和“結論”在一定條件下轉化，可得出有異于原型題的新題。

例2：如圖2，AE是△ABC外接圓的直徑，AB·AC=AD·AE，求證：AD⊥BC。

3.保留條件，引申結論，在保留原題條件的前提下，對其結論進行深入挖掘，可利用相關的知識導出新的結論或提出新的問題。

例3：如圖3，AD是△ABC的高，AE是△ABC外接圓的直徑，求證：S△ABC=1/2AD，AEsin∠BAC。

4.變更條件，推出新的結論。將例題、習題的條件減弱（或增強）或進行等價代換，使問題變得較為靈活，使結論具有一定的綜合性。

例4：如圖4，已知AD是△ABC的高，MN是△ABC的外接圓直徑，求證：AB·AC=AD·MN。

5.推廣變式，在原命題的條件進行引申，實施由特殊到一般或由一般到特殊的演變，從而獲得新命題。

例5：如圖5△ABC內接于⊙O，D在BC邊上，點E在CB上，且∠BAE=∠CAD，求證：AB·AC=AE·AD。

（三）習題處理要注意“轉化”

課本是教學的重要依據，立足于鉆研課本習題，往往起到舉一反三的效果，同時也培養了學生的發散思維能力和勇于探索的精神。

三、結合課改數學內容采用的模式，培養學生的創新能力

課改的數學內容采用“問題情境——建立模型——解釋、應用與拓展”的模式展開。讓學生經歷知識的形成與應用的過程，從而更好地理解數學知識的意義，掌握必要的基礎知識和基本技能，發展應用數學知識的意識與能力，增強學好數學的愿望和信心，進一步發展學生的創新能力。

（一）創設問題情境，激勵學生創新。在教學中，教師通過提出問題，激勵學生打破自己的思維定勢，從獨特的角度提出疑問，讓學生大膽地對教材上的內容質疑，敢于對教師的講解質疑。這樣批判性質疑正是創新思維的集中體現，任何科學的發明與創新正是通過批判性質疑開始。

（二）建模探索，提供有利于創新的學習環境。“數學教學是數學活動的教學”。數學活動是支撐數學課程目標體系的最佳支點，學生是數學活動的主體。因此，在教學過程中應該從學生已有的生活經驗出發，讓學生親身經歷將實際問題抽象成數學模型并進行解釋與應用的過程，進而使學生獲得對數學理解的同時，在思維能力、情感態度與價值觀等方面得到發展。

（三）數學知識的應用與拓展，潛移默化地培養學生的創新能力。課改專門設了“實踐與綜合應用”學習領域，強調通過“綜合實踐活動”這種新的學習形式，為學生提供運用數學知識提高分析問題，解決問題的意識和能力的機會，促進其經驗的積累，發展其創新意識和實踐能力。例如，某地生產一種綠色蔬菜，若在市場上直接銷售，每噸利潤為1000元，經粗加工后銷售每噸利潤可達4500元，經精加工后銷售每噸利潤漲至7500元。當地一家農工公司收購了這種蔬菜140噸，該公司加工的生產能力是：如果對蔬菜進行粗加工，每天可加工16噸;如果精加工，每天可加工6噸，但這兩種加工方式不能同時進行，而公司必須在15天內將這批蔬菜全部銷售，為此公司設計了三種可行方案：

方案一：將蔬菜全部進行粗加工。

方案二：盡可能多地對蔬菜進行精加工，沒有來得及時加工的蔬菜在市場上直接銷售。

方案三：將部分蔬菜進行精加工，其余蔬菜進行粗加工，并恰好15天完成。

你認為選擇哪種方案獲利最多？為什么？

這其實是一元一次方程的應用，它與如何獲取最大的利潤這樣的社會熱點問題聯系，無形變成立意新穎的探索型題，這樣更好地發展學生的創新能力。

總之，每個學生的思維都具有創新的潛能，因而教學過程對其潛能的啟發顯得尤為重要，課改內容中還編制很多開放性問題，新大綱要求我們改進教學方法、改變教學方式等等提供發揮創造才能的條件和氛圍，使數學教學變成一個生動、活潑、有創意的過程。正所謂“教學有法，但無定法”就是這個道理。培養創新能力與創新精神是新世紀的要求，作為一個數學教師應多渠道、多方位、多角度地挖掘、研究、使用教材中的創新思維因素;更要在課堂教學中去開發學生的創新潛能，培養學生的創新能力和優秀的創新品質。

責任編輯徐國堅