直面核心知識 關注理法相融
——小學數學運算能力培養例談

□凌璐予 徐丹紅

運算能力是數學學科核心素養的關鍵能力之一。對于小學數學教學而言，運算能力的培養是重中之重，也是基礎中的基礎。根據《義務教育數學課程標準（2011 年版）》對“運算能力”所做的明確的定義，我們可以這樣理解“運算能力”：運算能力不等同于計算能力，它不僅是會算、算正確，掌握算法，即知其然；還包括對于運算本身，也就是對算理的理解，即知其所以然，在此基礎上靈活選擇方法解決問題。因此算理的理解與算法的選擇是運算的重心。

一、調查分析找問題——運算能力現狀

聚焦掌握算法和理解算理，筆者對所在學校六年級的學生進行了測試，內容如圖1所示。題目一和題目二指向算理理解，題目三和題目四指向運算技能的掌握。

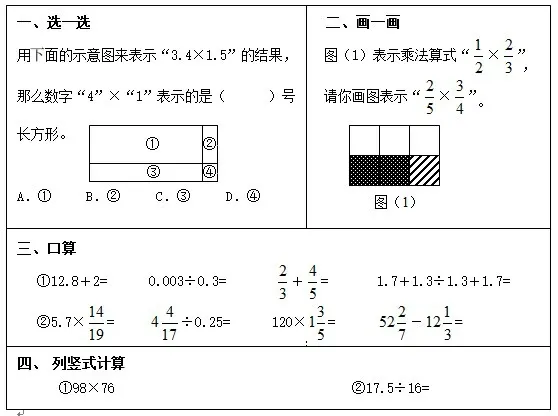
圖1

測試結果顯示，題目一的得分率為54.84%；題目二的得分率為61.29%；題目三口算第一行的得分率為89.52%，第二行的得分率為68.54%；題目四第①題的得分率為90.32%，第②題的得分率為79.42%。筆者對測試結果分析如下。

1.運算技能強于運算理解

從測試結果可以發現，題目三和題目四的得分率高于題目一和題目二，特別是口算第一行和豎式計算第一題，正確率高達90%左右。由此表明學生在解決純計算這類單一程序性題目時，能夠根據運算順序和運算法則正確地進行運算。相比之下，對于解決或解釋運算意義和算理的題目，學生并不能或者不能完全讀懂圖形的表征方式。這種鮮明的反差，或多或少地反映了學生運算學習的一種現狀，即運算技能強于運算理解。

2.運算理解影響運算技能

再看同樣是純口算的兩行，第一行正確率遠遠高于第二行，分析原因：一是碰到稍復雜的口算題，有些學生缺乏靈活選擇算法的能力，按部就班，因計算煩瑣而出錯；二是有些學生意圖選擇合理的算法計算（如圖2），但方法運用錯誤，究其原因是對算理理解不到位，即運算理解影響了運算技能。

圖2

二、追根溯源尋方法——運算能力培養

算法、算理是運算能力的一體兩翼。尤其在小學數學中，兩者相輔相成，不可偏廢。因此，教師在課堂上應尋求算法與算理的平衡點，以核心知識入手，循理入法，以法馭理。

（一）以“整體”尋“核心”，重組內容

《浙江省小學數學教學建議》指出：“教材研讀要關注整套教材的基本結構，研讀單元教學內容，合理劃分課時，充分考慮知識形成線索和學習認知線索，在此基礎上通過補充、修改、調換、刪減等方法完善教材資源。”因此，以單元視角尋找單元核心并在此基礎上重組內容，能更好地凸顯教學內容本質，計算教學亦是如此。以人教版三年級下冊《除數是一位數的除法》為例。

1.單元分析，把握整體

此單元的主要內容有：口算除法、筆算除法和用估算解決問題，在口算除法中安排了三個例題：60÷3，120÷3，66÷3；在筆算除法中也安排了三個例題：42÷2，52÷2，256÷2。那這六道題核心知識間的聯結點在哪里？不論是口算除法還是筆算除法，其實質都是平均分，核心是怎么分。區別在于表達方式不同：口算除法把分的過程用橫式表示，而筆算除法將分的過程用豎式表達。在口算除法中弄清分的過程，能為筆算除法做好鋪墊，因此熟練掌握口算除法至關重要。

2.學生分析，把握起點

為了了解三年級學生這一單元知識的學習起點，筆者對兩所學校（一所農村小學、一所市區小學）的三年級學生做了一次小調查（如圖3）。

圖3

調查結果顯示，第1小題，市區小學學生的正確率為97.09%，農村小學學生的正確率為90.23%。以下具體呈現第2小題的調查結果（如下表）。

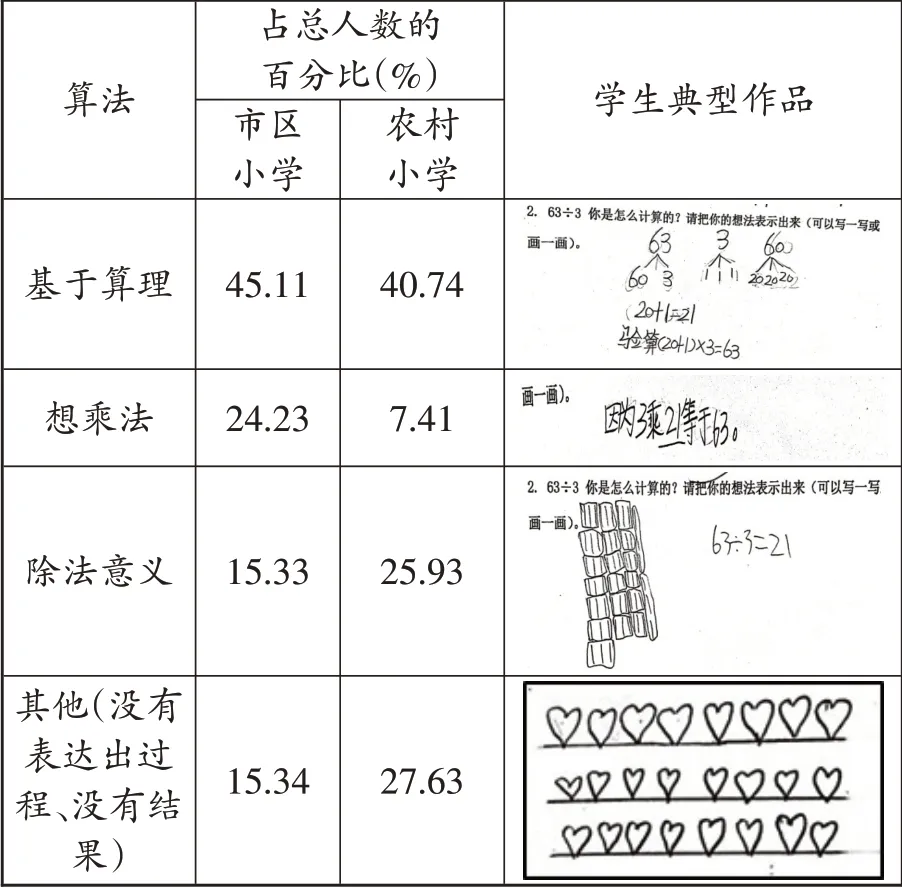
算法基于算理想乘法除法意義其他（沒有表達出過程、沒有結果）占總人數的百分比（%）市區小學45.11 24.23 15.33 15.34農村小學40.74 7.41 25.93 27.63學生典型作品images/BZ_14_815_500_1177_658.pngimages/BZ_14_812_670_1181_755.pngimages/BZ_14_819_767_1174_965.pngimages/BZ_14_816_977_1176_1174.png

分析以上調查結果可知：無論是市區小學還是農村小學，8 道口算題的正確率都比較高，表明學生對口算除法掌握得很好，對基本的算理也比較清晰，因此這不該是教學的重心，如果仍將教材的這幾道口算題貫穿口算除法教學，那起點是否太低了？

當然，高正確率并不意味著口算除法的教學可以完全舍棄。第2小題調查結果顯示，百分之四十幾的學生能基于算理把分的過程表示出來，但在完成第3小題時，卻只有26.31%的學生能正確表述分的過程，有11.25%的學生是將42 拆分成40 和2 后平均分的，其余的學生則無從下手。為什么學生對63÷3 的算理表述得那么清晰，但對42÷3 卻不知所措呢？究其原因是學生對分的過程并不清楚，只是停留在機械的模仿上，把被除數拆成十位和個位再除以3，將這樣的方式遷移到42÷3 上，就會出現40÷3的情況。而類似“42÷3”這樣的題是被安排在筆算除法的例2進行教學的，學生在計算這類筆算題時錯誤率比較高，那是因為在不理解算理的情況下直接進行筆算是有一定難度的。所以，是否可以在口算部分增加筆算除法例2 的口算教學？這樣既能解釋算理，也為筆算除法的學習做鋪墊。

3.重組內容，把握核心

基于單元視角和學生的學情分析，我們對第一課時“除數是一位數的口算除法”做了以下調整。

第一環節：將教材編排的口算作為課前熱身，并將算理進行初步表征；第二環節：探究42÷3的口算方法，跟進練習84÷3，并進行對比，凸顯算理；第三環節：練習，例題內容鞏固。

重組凸顯兩個方面的意圖：一是減少類似“60÷3”這樣的口算練習，避免重復教學導致學生感到無趣現象的出現。二是加強類似“42÷3”這樣的口算訓練，既能更好地幫助學生理解算理，防止機械模仿，又能突破筆算除法例2 的教學難點，為后面的學習做好鋪墊。

（二）以“事理”明“算理”，循理入法

在真真切切的情境操作中慢慢感知、逐步體驗更符合小學生的認知規律。因此，教師可通過直觀的操作活動將抽象的算理具體化、形象化，循“理”入“法”，以“理”馭“法”，實現“感悟”算理到“生成”算法的跨越。

1.借直觀學具，以“事”明“理”

借助學具可將算理清晰地進行表述，從而更好地掌握算法。如在上述探究42÷3 的過程中，可以先留時間讓學生想一想。然后讓學生借助小棒分一分，將42 分成3 份的過程動態地、直觀地予以呈現。同時提出兩個核心問題：“你是怎么分的？”“余下的1捆怎么辦？”這樣既聚焦難點，又使教學變得簡潔明了。

2.借幾何模型，以“圖”明“理”

幾何模型能將抽象的算理直觀化。如在教學“兩位數乘兩位數”的例題14×12 時，可借助點子圖清晰地展示不同豎式其算理的內涵：圖4-1表示先分別計算10個14和2個14，再把積相加；圖4-2表示先分別計算4 個12 和10 個12，再把積相加。結合學生所熟悉的表格顯示口算過程，再溝通點子圖、口算乘法與乘法豎式之間的內在聯系，實現算法與算理的有效融合。這樣不僅幫助學生在算理意義建構的基礎上理解算法，還培養了學生使用直觀模型進行思考的意識，獲得解決新問題的策略和方法。

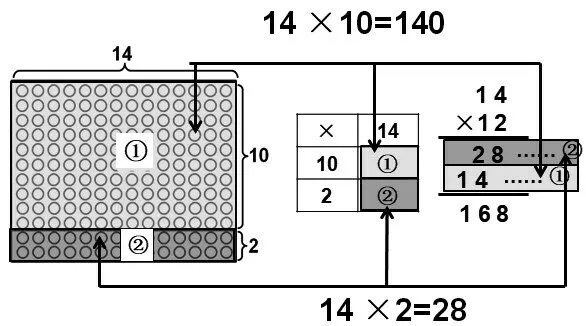
圖4-1

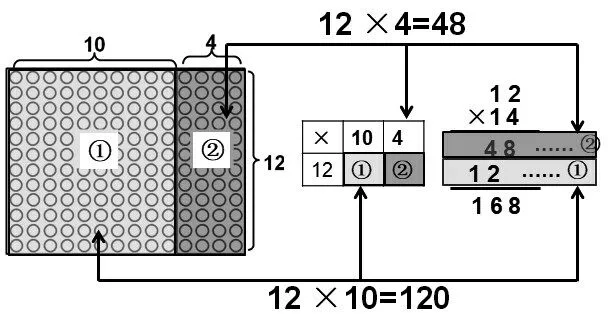
圖4-2

如果對每一步中的兩位數乘一位數和兩位數乘整十數再進行拆分（如圖5），就會發現這兩種算法的過程是一樣的，只是順序不同而已。學生從點子圖中能清晰地看到表格和豎式中每一小步表示的意思，對抽象的算理自然就明白了。有了這樣的直觀模型，把整數乘法遷移到小數乘法（圖1 中的題目一）就水到渠成了。

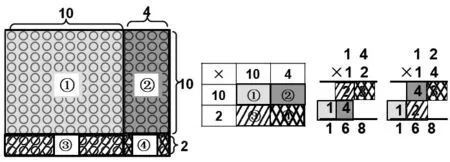
圖5

（三）以“不變”應“萬變”，凸顯主干

教師在日常運算教學中常常鼓勵學生探索不同的算法，意在開闊學生的思維，體會算法的多樣性，這是培養學生思維能力的有效途徑。但應該明確的是，追求算法多樣化本身并不是目的，在“數的運算”教學中，不能過于渲染缺乏遷移價值的多種算法而干擾運算的主干算法。

1.選擇學習材料，強化主干

比如在上述《除數是一位數的口算除法》中，如果用32÷2 作為探究口算除法的材料，學生會出現兩種算法：（1）20÷2=10，12÷2=6，10+6=16；（2）30÷2=15，2÷2=1，15+1=16。兩種算法都能得到準確結果，但第二種算法具有局限性，而第一種算法能為后續筆算做鋪墊。如果要凸顯第一種主干算法，那么32÷2這一口算材料顯然就不太合適，而采用42÷3 就能迫使學生選擇算法（1），因為40÷3 是有余數的，學生自然會舍棄算法（2）。由此可見，選擇合適的學習材料，凸顯主干方法，能幫助學生深刻理解算理，也能為筆算做鋪墊。

2.鼓勵方法變式，靈活算法

凸顯主干方法并不意味著“死板”和“一成不變”。我們常說算法的選擇應根據內容、數據而定，合理、靈活地選擇算法才是運算能力的體現。但這樣的合理與靈活，往往是建立在對主干算法深刻理解的基礎上的，從而衍生出基于主干算法的變式。比如三位數乘一位數的筆算方法中，大部分學生是這樣列豎式計算的（如圖6），這是三位數乘一位數的主干算法。但是像這樣連續進位的筆算錯誤率會比較高，究其原因是小學生頭腦中儲存信息的能力有限，他們把注意力放在暗記進位的數字和乘加運算上了。學生長時間進行這樣的計算，會不自覺地把思維的重心偏向乘加進位口算技能，而弱化對乘法算理的理解。為了避開因乘加而造成的計算困擾，可以采用下列方法（如圖7）。

圖6

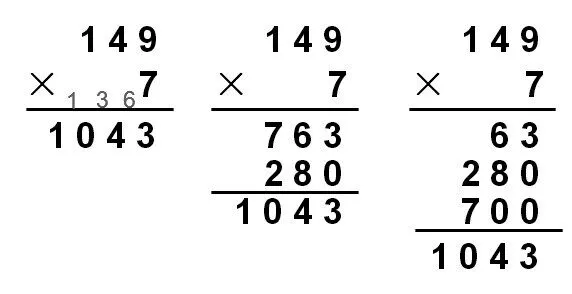
圖7

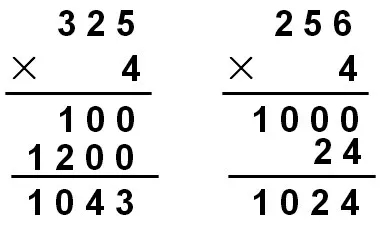
圖8

這兩種方法和列豎式方法體現的算理是一樣的，都是拆分149，其中左邊的方法是拆成7 個109和7 個40，我們把這種方法稱為“踢十法”，這樣就減輕了學生的思維負擔，沒有了乘加兩步計算，不僅正確率能有所提高，而且學生把思維的重心放在了算理上。有了“踢十法”，學生還會遷移運用“踢百法”“踢個法”，所以在解答其他筆算題目時，學生出現了圖8的做法。

總之，在數的運算教學中，教師不僅要關注學生運算技能的掌握，更要關注學生理解算理、掌握算法的學習過程。只有將算理與算法有機融合，才能更好地培養并發展學生的運算能力。

參與文獻：

[1]董文彬.從運算能力走向運算素養——關于運算及運算教學的思考[J].教育科學論壇，2019（28）.

[2]曹培英.跨越斷層，走出誤區：“數學課程標準”核心詞的解讀與實踐研究[M].上海：上海教育出版社，2017.

[3]楊金風.內蒙古自治區五年級學生數學運算能力現狀及發展[D].北京：中央民族大學，2016.

[4]黃翔.理解把握數學課程標準中的核心概念（二）——《義務教育數學課程標準（2011 年版）》解析之四[J].小學數學教育，2012（7-8）.