叢林飛車速度計算分析及研究

趙九峰，馬寧，陽先波，張勁松

叢林飛車速度計算分析及研究

趙九峰1，馬寧2，陽先波2，張勁松2

（1.河南省特種設備安全檢測研究院，河南 鄭州 450000；2.中國特種設備檢測研究院，北京 100029）

以叢林飛車為例，通過理論計算和虛擬樣機技術，模擬滑行最大速度在不同摩擦系數下的仿真結果，表明輪軌系統的摩擦系數對叢林飛車的速度影響至關重要，討論了滾動摩擦產生的機理，同時分析了影響摩擦系數的因素，根據力矩平衡推導出滾動摩擦系數的計算公式，說明滾動摩擦阻力不僅與法向載荷有關，而且與滾動體的材料、硬度及輪子半徑等因素有關，為滑行車類游樂設施速度計算提供參考。

大型游樂設施；叢林飛車；能量守恒定律；虛擬樣機；滾動摩擦力臂

在游樂設備機構系統中，大量構件處于運動之中，構件運動的某些時刻處于最危險的工況。于是需要對游樂設備中的構件進行強度分析。先使用多體動力學軟件進行剛體動力學分析，得到連接處的約束力，然后再在有限元軟件中對感興趣的構件劃分網格，并導入從動力學軟件中得到的載荷，對之進行靜強度分析[1]。

滑行車類游樂設施速度高、運動形式富于變化，其作為游樂設備之王深受廣大游客的喜愛。滑行車是利用自身的初始重力勢能完成運動，其運行過程中的運動學和動力學性能直接決定了其安全性。滑行車類游樂設施的基本工作原理是能量守恒定律，對其進行運動學分析，通過計算軌道不同處的車速，可以獲取滑車與軌道的相互作用情況[2-3]，獲取滑車和軌道的最危險工況，因此，速度計算是滑行車類游樂設施計算的前提。本文以叢林飛車為例，討論了滾動摩擦產生的機理，分析了影響摩擦系數的因素，為滑行車類游樂設施速度計算提供參考。

1 叢林飛車的設計原理

如圖1所示，叢林飛車采用了過山車的設計方式，由滑車和軌道組成，為單軌滑行車的結構型式，為了保證滑車始終沿空間軌道運行、完成各種預定動作，其輪系關系不同于一般的軌道車輛。軌道由無縫鋼管和翼板焊接而成，滑車由輪架支承，輪架上裝有行走輪、下導輪、側導輪三組車輪，分別沿不同方向將車輛約束到軌道上，使其始終不會脫離軌道[4]。

滑軌通過多處吊點吊掛于基礎梁或基礎柱上，在其滑行路線上設置出發站臺和到達站臺，兩站臺間存在高度差，利用自重，游客可乘坐滑車從出發站臺自由滑行至到達站臺，滑車一般會通過滑車回收系統牽引至出發站臺。滑車的車體被軌道限制了某些自由度，只能沿著特定的軌道運行，時而急速下滑，時而急速轉彎，超重、離心等現象不斷出現。

叢林飛車運行時，乘客在重力作用下，沿軌道向下運動，可以簡化成為一種簡單物理運動模型，由于叢林飛車大多沿環形軌道運行，因此可忽略風載荷的影響。

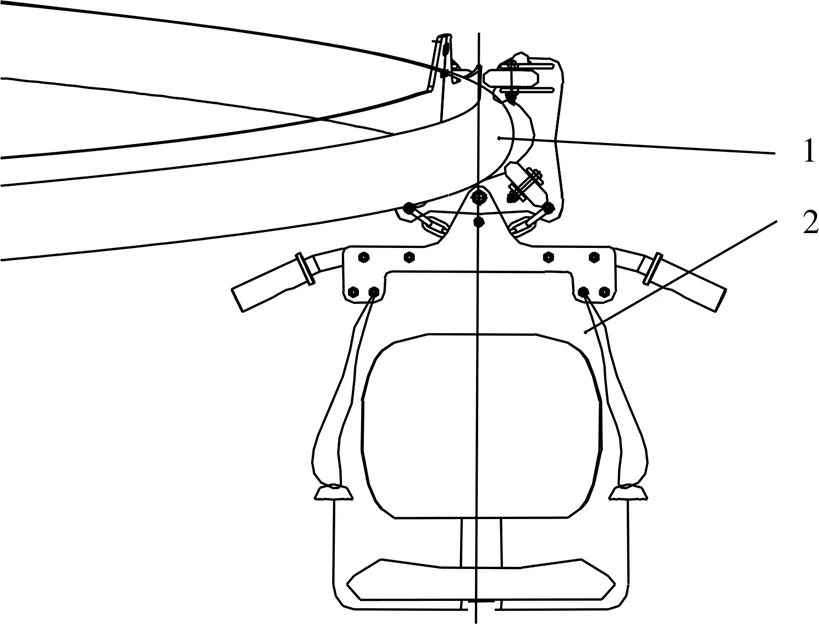
1.軌道 2.滑車

如圖2所示，質量為的物體（為滑車和乘人的總質量，kg），沿坡度下滑過程中，根據下滑段各特征點（坡度和是否轉彎）劃分為段。其中第（＝1,2,…,）段，下滑高度為H，下滑坡長為S，滑車在軌道上受到的摩擦阻力為滾動摩擦，摩擦系數為。

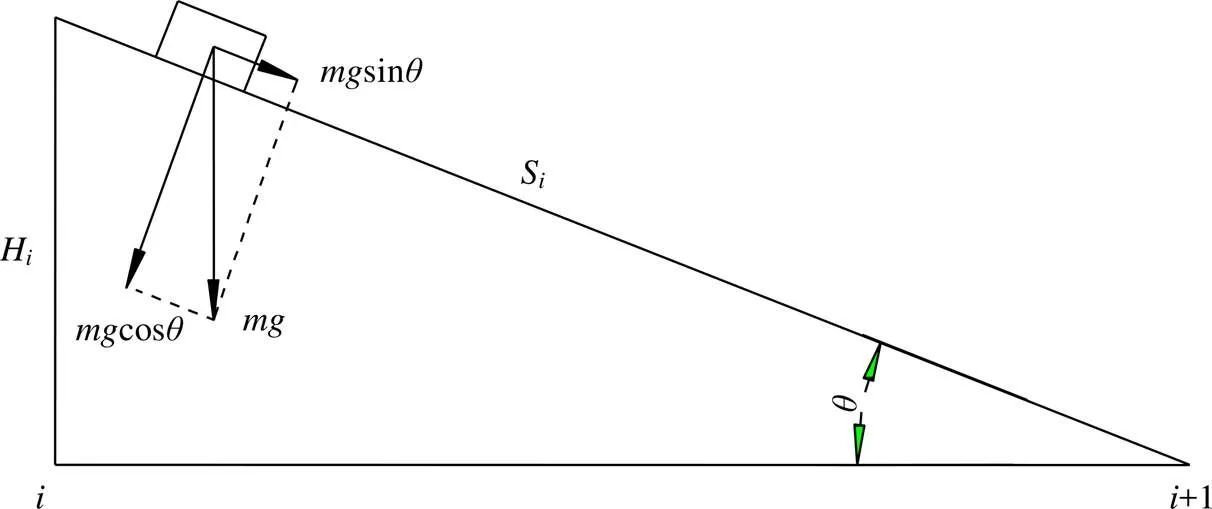
圖2 叢林飛車運行載荷示意圖

則滑車沿軌道下滑過程中，有：

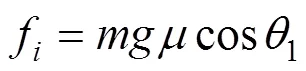
式中：f為滑車承受的摩擦力，N；θ為第段軌道坡度，即軌道與水平面的夾角，°；為標準重力加速度，9.8 m/s2。

滿載工況下，滑車由靜止狀態從高處滑落的過程中（1＝0 m/s），根據能量守恒定律有：

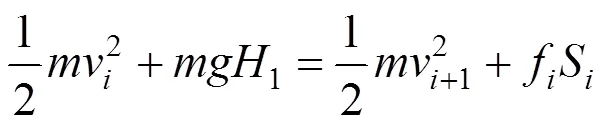
式中：H為第段下行軌道最高落差，m；S為第段下行軌道長度，m。

聯立式（1）、式（2）可得求得滑車各段的滑行速度：

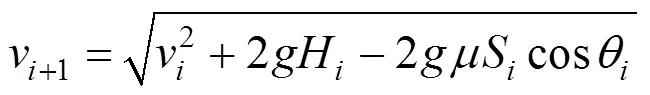
由式（3）可知，叢林飛車的速度僅與軌道的落差、長度、坡度和摩擦系數有關，而與物體的質量無關。

2 實例驗算

本文以80 m長度的叢林滑車為研究對象，軌道根據坡度分為兩段，摩擦系數＝0.04。軌道的參數如表1所示，計算叢林滑車的各段運行速度。

表1 軌道分段表

由式（3）可得，第一、第二段軌道的線速度依次為：

2＝5.25 m/s

3＝4.66 m/s

計算可知，叢林滑車在軌道上運行到軌道第一段尾部時，速度達到最大值5.25 m/s，然后可根據最大速度確定叢林滑車的沖擊系數，進而對滑車和軌道進行各種工況的校核計算。

3 叢林飛車的動力學分析

結構動力學分析通過虛擬實驗精確、快捷地預測產品的整機性能，使產品設計人員在各種虛擬環境中，真實模擬產品整體的運動及受力情況，更好地理解機械系統的運動，精確預測載荷變化，計算其運動軌跡、速度和加速度等[5]。

多剛體動力學分析的基礎是拉格朗日方程。動力學分析軟件只是基于力學、數學、物理學模型的一種計算工具，ADAMS、ANSYS Rigid Dynamics等虛擬樣機商業軟件，可以進行靜力學、運動學和動力學分析等，直接影響仿真結果的是仿真輸入數據的正確性，而非軟件本身。本文利用ANSYS Rigid Dynamics進行動力學仿真分析計算。

3.1 仿真模型與約束

滑車由最高點沿軌道自由滑行，將滑車簡化為質點，結合叢林飛車的結構特點，對叢林飛車簡化動力學建模的過程進行三種假設：

（1）滑車和軌道均為剛體，滑車模型簡化為一個滾輪；

（2）下滑全程，滾輪和軌道始終接觸良好；

（3）忽略輪軌系統的熱變形和摩擦系數隨溫度的變化[6]。

模型由滑車和軌道組成，忽略其他零部件，叢林飛車的簡化模型如圖3所示。

圖3 叢林飛車簡化模型

利用軟件約束工具（Point on Curve），定義滑車沿軌道曲線運動，由于軌道分為兩段，不同坡度對應的摩擦力不同，定義點線副的約束載荷的分段函數模擬摩擦力，摩擦力的方向為軌道曲線的切線方向。軌道施加固定約束（Fixed），林飛車在整個運行周期內，始終受到重力的作用，施加標準重力加速度，方向向下，如圖4所示。

3.2 仿真分析

仿真時間＝21 s，通過仿真分析，在摩擦力作用下，滑車沿軌道運行的線速度曲線如圖5所示。由圖5可知，滑車的最大線速度為5.25 m/s，終點的線速度為4.66 m/s，與理論計算速度一致，表明了仿真過程、運動狀態的正確性，也表明仿真計算結果的合理性[7]。

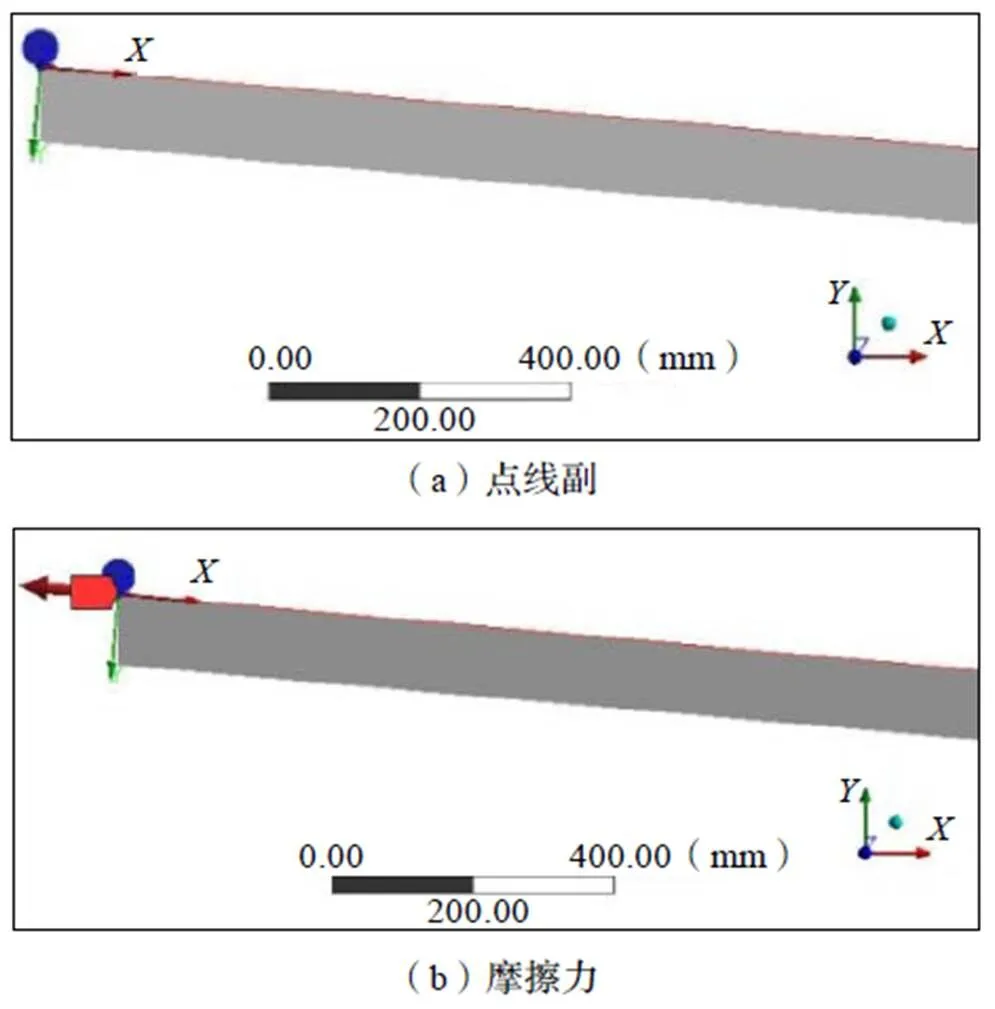
圖4 載荷與約束

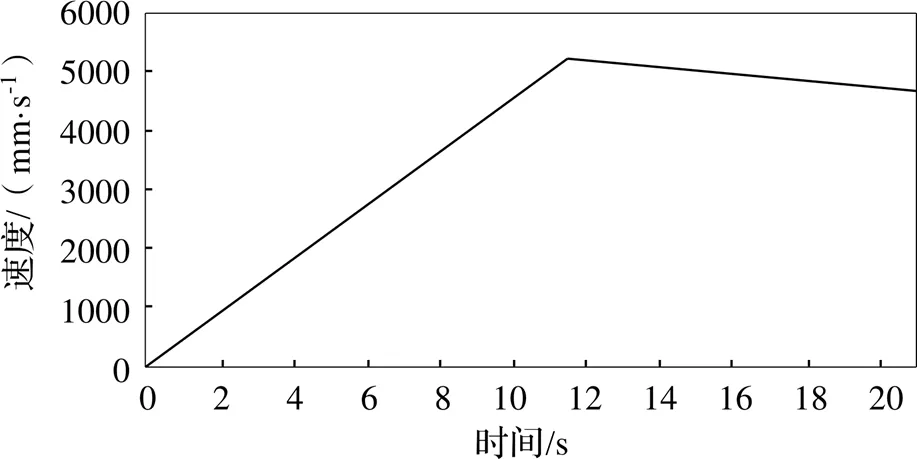
圖5 速度曲線

4 滾動摩擦

滾動摩擦力是物體滾動時，滾動接觸面所受的摩擦力。滾動摩擦與滑動摩擦有著本質區別，18世紀初，庫倫首先闡明古典滑動摩擦定理后，開始對滾動摩擦機理進行探索，于1785年發表滾動摩擦定理，并導出了有量綱的滾動摩擦力臂[7]。

滾動摩擦的產生是由于物體和平面接觸處的形變引起的。物體受重力作用而壓入支承面，同時本身也受壓縮而變形，因而在向前滾動時，接觸前方的支承面隆起，這使得支承面對物體的彈力的作用點從最低點向前移，所以彈力與重力不在一條直線上，而形成了一個阻礙滾動的力偶矩，如圖6所示。

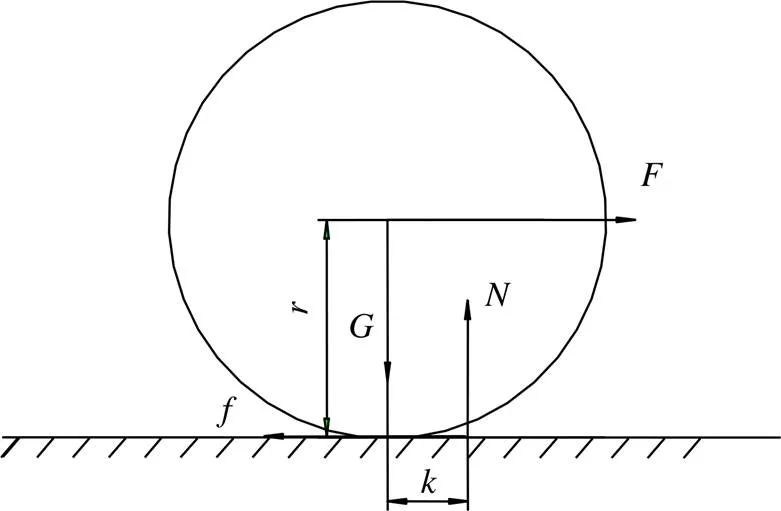
圖6 車輪載荷示意圖

根據力矩平衡，有：

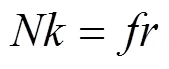
式中：為滾動摩擦力臂，mm；為車輪半徑，mm；為滾動摩擦力，N；為支承面對物體的彈力，N。

則由式（4）可得：

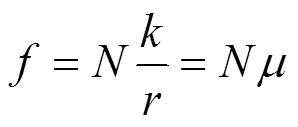
式中：＝/為摩擦系數，與滾動物體和支承面的材料、硬度以及輪子半徑等因素有關。

接觸面愈軟，形狀變化愈大，則滾動摩擦力就愈大。叢林飛車的滑車沿軌道下滑過程中，受到的阻力主要是滾動摩擦力。叢林飛車輪子多為尼龍、聚氨酯等高分子材料，由《機械設計手冊》[8]表1-1-10可知，滾動摩擦力臂＝0.8～1.2 mm（介于摩擦副為圓柱形車輪、橡膠輪胎與混凝土地面之間），滑車輪子的半徑＝20～40 mm。因此叢林飛車中滑車在軌道上運行的摩擦系數在0.02～0.06之間。為了研究不同摩擦系數對滑車最大速度的影響，取摩擦系數為0.02、0.04、0.06分別進行動力學仿真計算。仿真得到最大速度的曲線如圖7所示。

由圖7可知，隨著摩擦系數的增大，滑車的最大速度明顯減小，最大速度由7.28 m/s下降到3.96 m/s，降了近一半，表明滑車的最大速度對摩擦系數很敏感，因此在對叢林飛車進行速度計算時，確定滑車與軌道的摩擦系數是關鍵。

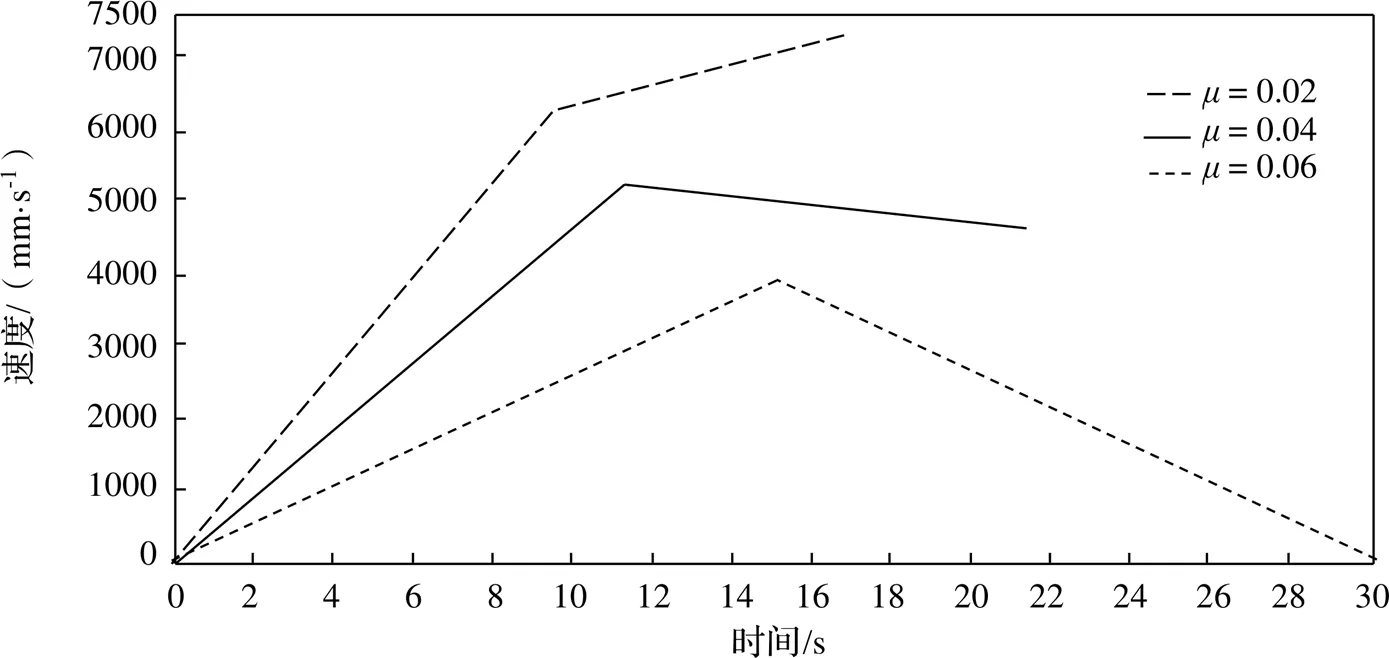
圖7 不同摩擦系數對滑車速度的影響

現有的叢林飛車運動學和動力學分析，都是根據經驗給定輪軌系統的摩擦系數，實際的摩擦系數與輪子和軌道的材料、硬度以及輪子半徑等因素有關，而不同廠家的產品中，輪子的材料各種各樣（如尼龍、聚氨酯等），軌道的材料也不同（如碳鋼、不銹鋼等），所以叢林飛車輪軌系統摩擦系數需根據樣機運行試驗取值，以保證仿真的真實性，提高叢林飛車的整體設計水平。

5 結語

滑行類游樂設備的實際運行工況復雜多樣，本文以叢林飛車為例，依據能量守恒定律對滑車的運行速度進行了理論計算，給出了一些參數和計算公式以確定各段的速度。虛擬樣機仿真計算速度與理論結果比較，表明計算結果的可靠性和正確性。通過滑行最大速度在不同摩擦系數下的仿真結果對比，表明輪軌系統的摩擦系數對滑車速度的影響至關重要。同時分析了影響摩擦系數的因素，其計算方法可供滑行類游樂設施速度計算提供參考。

[1]彭禮輝，李光. ADAMS和ANSYS對機構的聯合仿真分析[J]. 湖南工業大學學報，2012（2）：43-48.

[2]宋海洋，屈福政. 過山車輪軌摩擦實驗臺設計及動態性能研究[J]. 冶金設備，2013（1）：43-46.

[3]張勇，秦平彥，林偉明，等. 大型游樂設施運行狀態測試系統及關鍵技術研究[J]. 中國安全科學學報，2008（12）：166-171.

[4]王紅軍，王瑋瑋. 基于Delphi和OpenGL的原子滑車軌道設計平臺研究[J]. 微計算機信息，2009（10）：257-259.

[5]趙九峰. 基于ANSYS Workbench大擺錘剛體動力學分析[J]. 機械研究與應用，2019（1）：44-47.

[6]趙九峰. 基于ANSYS Workbench自控飛機回轉機構驅動功率的計算及電機選型[J]. 機械，2019（4）：30-33.

[7]汪志城. 滾動摩擦機理和滾動摩擦系數[J]. 上海機械學院學報，1993（4）：35-43.

[8]成大先. 機械設計手冊[M]. 北京：化學工業出版社，2016.

Analysis and Research on Speed Calculation of Jungle Flying Train

ZHAO Jiufeng1，MA Ning2，YANG Xianbo2，ZHANG Jinsong2

( 1.Special Equipment Safety Inspection and Research Institute of Henan Province, Zhengzhou 450000, China; 2.China Special Equipment Inspection and Research Institute, Beijing 100029, China )

Taking the jungle flying as an example, the theoretical calculation and virtual prototyping technology are used to simulate results of the maximum speed under different friction coefficients, show that the friction coefficient is crucial to the speed of the jungle speed, explore the mechanism of rolling friction, and the influence of friction coefficient Factors were analyzed. The calculation formula of the rolling friction coefficient is derived according to the moment balance, which indicates that the rolling frictional resistance is not only related to the normal load, but also related to the material, hardness and wheel radius of the rolling element, which provides a reference for the speed calculation of scooter type rides.

large-scale amusement device；jungle flying；energy conservation law；virtual prototype；rolling friction arm

X924；G248

A

10.3969/j.issn.1006-0316.2020.03.005

1006－0316 (2020) 03－0026－05

2019－09－16

趙九峰（1981－），男，河南平頂山人，碩士研究生，CAD/CAE工程師、檢驗師，主要從事游樂設備設計計算、特種設備結構仿真與載荷響應研究工作。