空氣質量數據校準研究

董文雷 馬一凡 徐海東

（石家莊鐵路職業技術學院 河北石家莊 050041）

1 模型分析

利用excel對國控點數據和自建點數據進行處理，發現國控點數據在時間上存在不連續性，有多天連續數個小時沒有數據，國控點共有4200條數據，比自建點少了700多條；自建點數據時間上也存在不連續且有重復數據的現象。采用刪除互不存在的數據，使國控點與自建點在時間上的數據同步匹配。再通過國控點與自建點“四氣兩塵”（PM2.5、PM10、CO、NO2、SO2、O3）的濃度值和環境空氣質量指數（AQI）指數對比畫出折線圖，通過折線的趨勢和吻合度進行分析。國控點與自建點進行數據統計時均采取單位時間平均值。計算環境空氣質量指數（AQI）值時，O3取日1小時最大值和8小時滑動平均最大值。

利用國控點數據與自建點數據的差值與自建點天氣因素數據進行相關系數比較，得出結論。

對國控點與自建點數據差值以小時為單位，建立多元線性回歸方程模型，并進行回歸分析。若效果不明顯，采用剔除異常點和建立二元線性回歸方程模型，進行回歸分析，直到得到理想結果。

2 模型的建立與求解

2.1 問題一

以x軸為時間軸，以y軸為各空氣污染物數據，建立自建點與國控點濃度值的比較，利用Matlab軟件進行數據分析，建立圖形并對比（這里只給出PM2.5和PM10濃度值對比），具體如下：

2.1.1 濃度值對比

（1） PM2.5濃度值對比

觀察圖1可知：在這一段時間內，雖然PM2.5自建點與國控點的濃度值曲線變化波動較大，但二者重合度相對較好，自建點濃度值大于國控點濃度值。

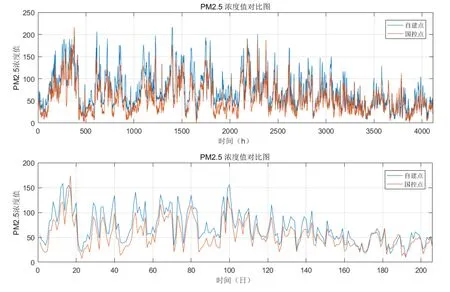
圖1 PM2.5濃度值對比

（2）PM10濃度值對比

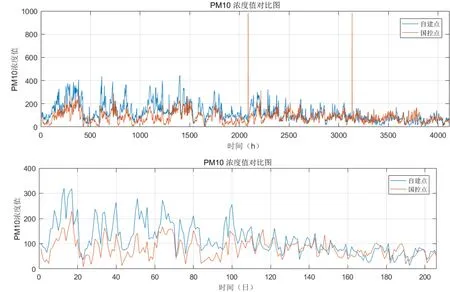
圖2 PM10濃度值對比

觀察圖2可知：在這一段時間內，PM10自建點與國控點的濃度值曲線變化相差無幾（在2018年11月到2019年3月濃度值曲線上下浮動較大，在2019年3月到2019年6月濃度值曲線上下浮動較小），且在2018年11月到2019年3月自建點濃度值大于國控點濃度值，在在2019年3月到2019年6月二者濃度值相差較小。小時的濃度對比圖中，有2處出現明顯異常。

2.1.2 濃度差值變化（國控點-自建點）（這里只給出ΔPM2.5和ΔPM10濃度值對比）

（1） ΔPM2.5變化

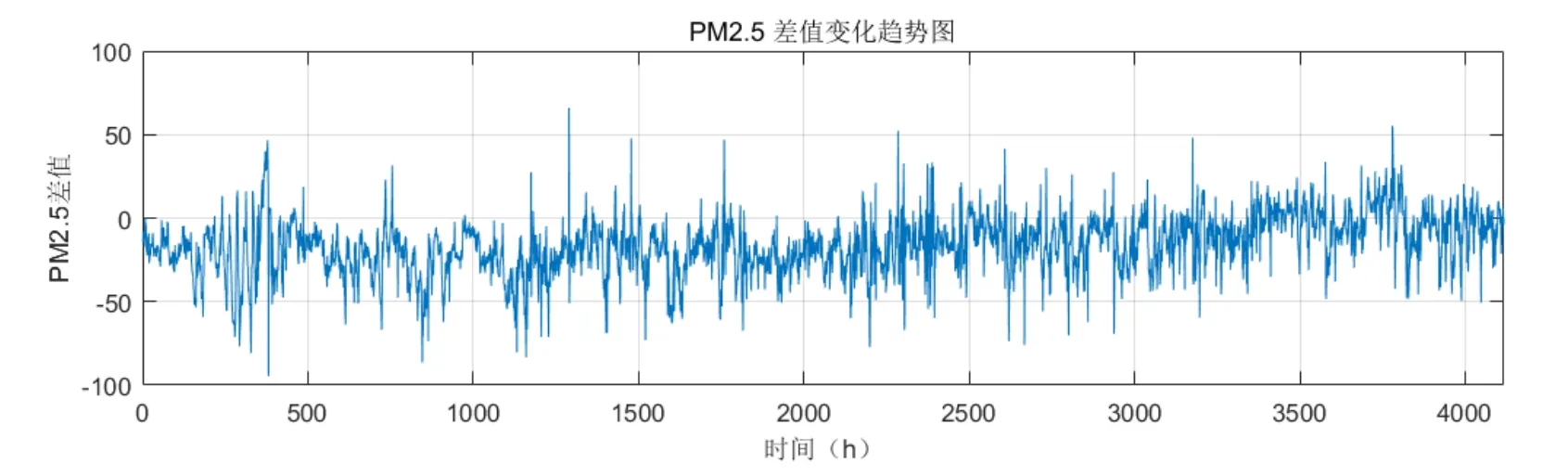
圖3 ΔPM2.5變化

由圖3可知：自建點數據值高于國控點，且時間越往后相差越小，數據變化較為穩定。（2）ΔPM10變化：

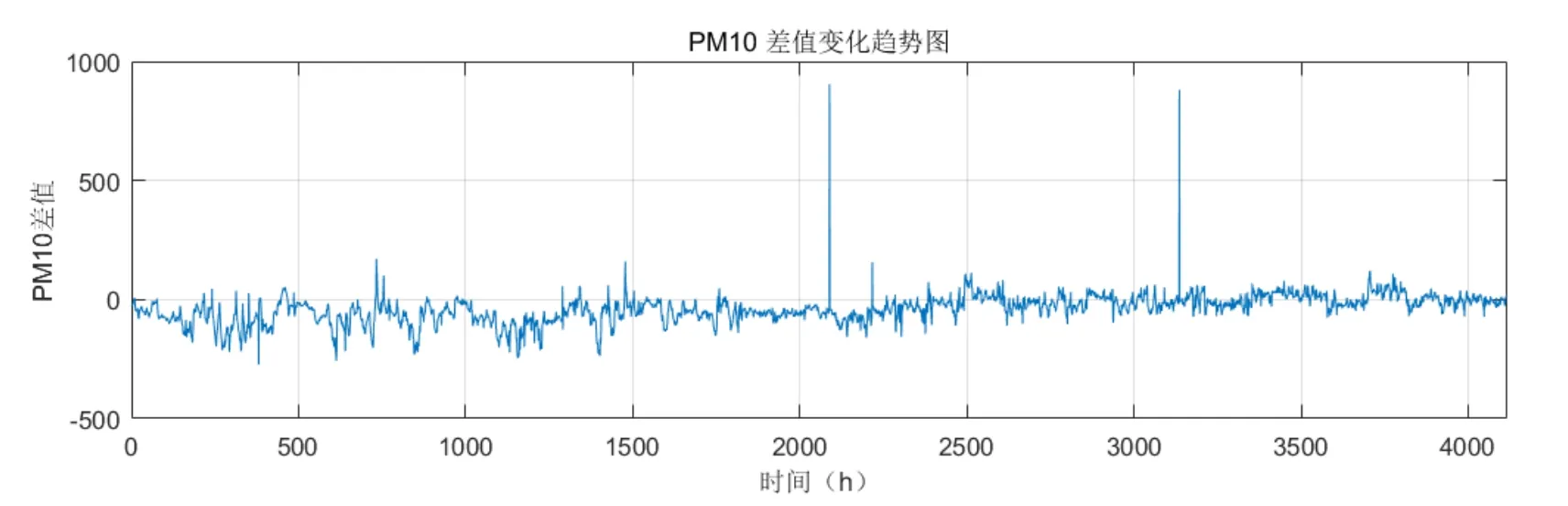
圖4 ΔPM10變化

由圖4可知：2018年11月到2019年3月自建點數據值高于國控點，2019年3月到2019年6月國控點數據值高于自建點，且在2019年3月左右和2019年4月左右出現2處異常數據。

2.2 問題二

建立基于Pearson 簡單相關分析的模型。通過對試題附件1.CSV和附件2.CSV中所給數據，以小時為單位，分類匯總得到4116組相關數據。將電化學氣體傳感器產生的零點漂移、量程漂移以及非常態氣態污染物(氣)濃度變化對傳感器的干擾看成關于時間t的函數，考慮到氣象參數溫度、濕度、風速、氣壓、降水，這6個因素對導致國控點與自建點數據影響的不確定性，利用 Matlab軟件計算，得到“兩塵四氣”改變量ΔPM2.5、ΔPM10、ΔCO、ΔNO2、ΔSO2、ΔO3對于每個影響因素的相關系數r值如表1和表2。

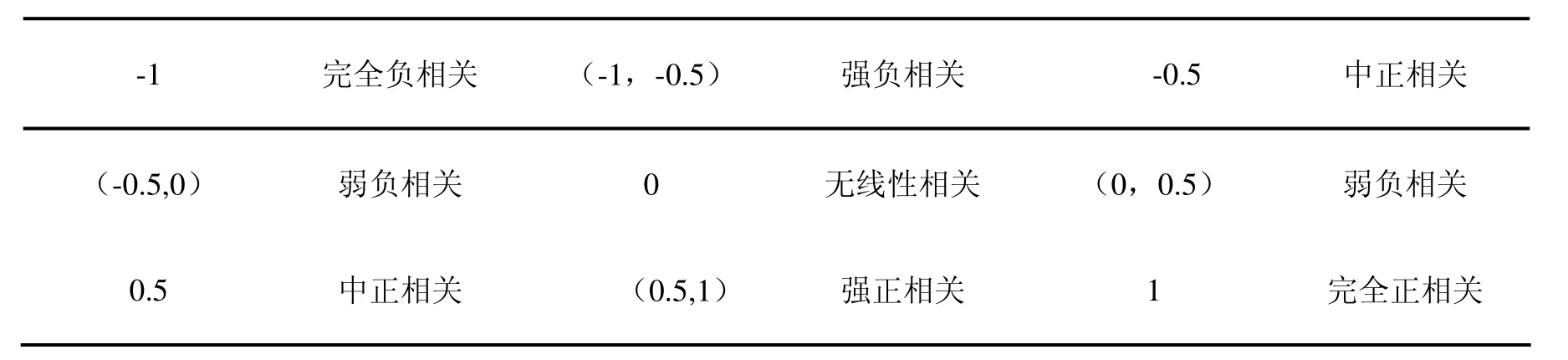
表1 相關系數r的性質

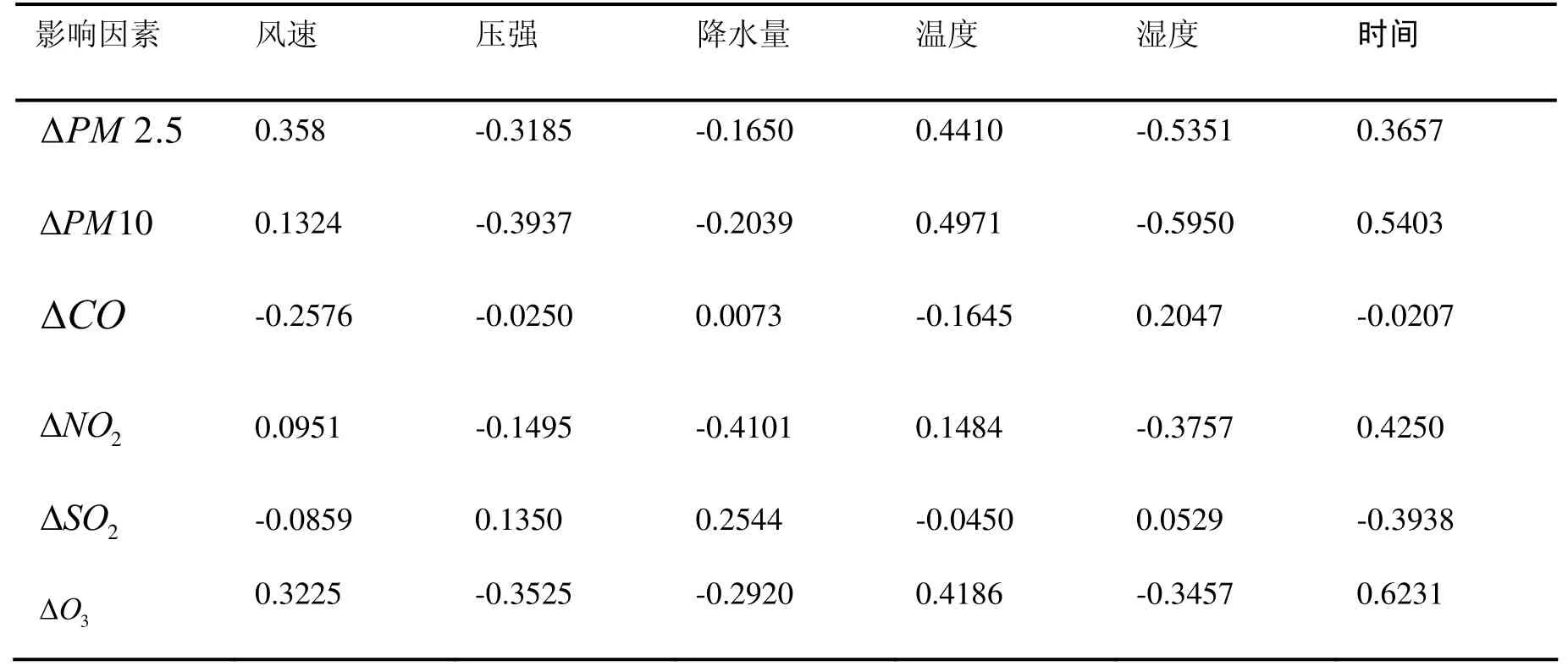
表2 不同影響因素的相關系數r值

2.3 問題三

首先建立多元線性回歸方程如下：

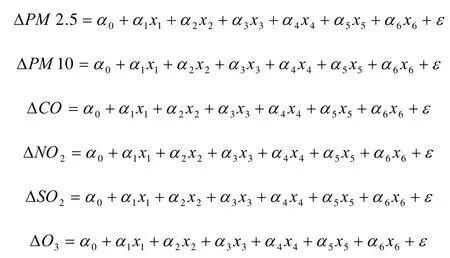
其中，α0，α1，α2，α3，α4，α5，α6為方程的回歸系數，x1，x2，x3，x4，x5x6分別代表溫度、濕度、風速、氣壓、降水和時間，計算得回歸系數α0，α1，α2，α3，α4，α5，α6見下表：決定變量R2如下表：

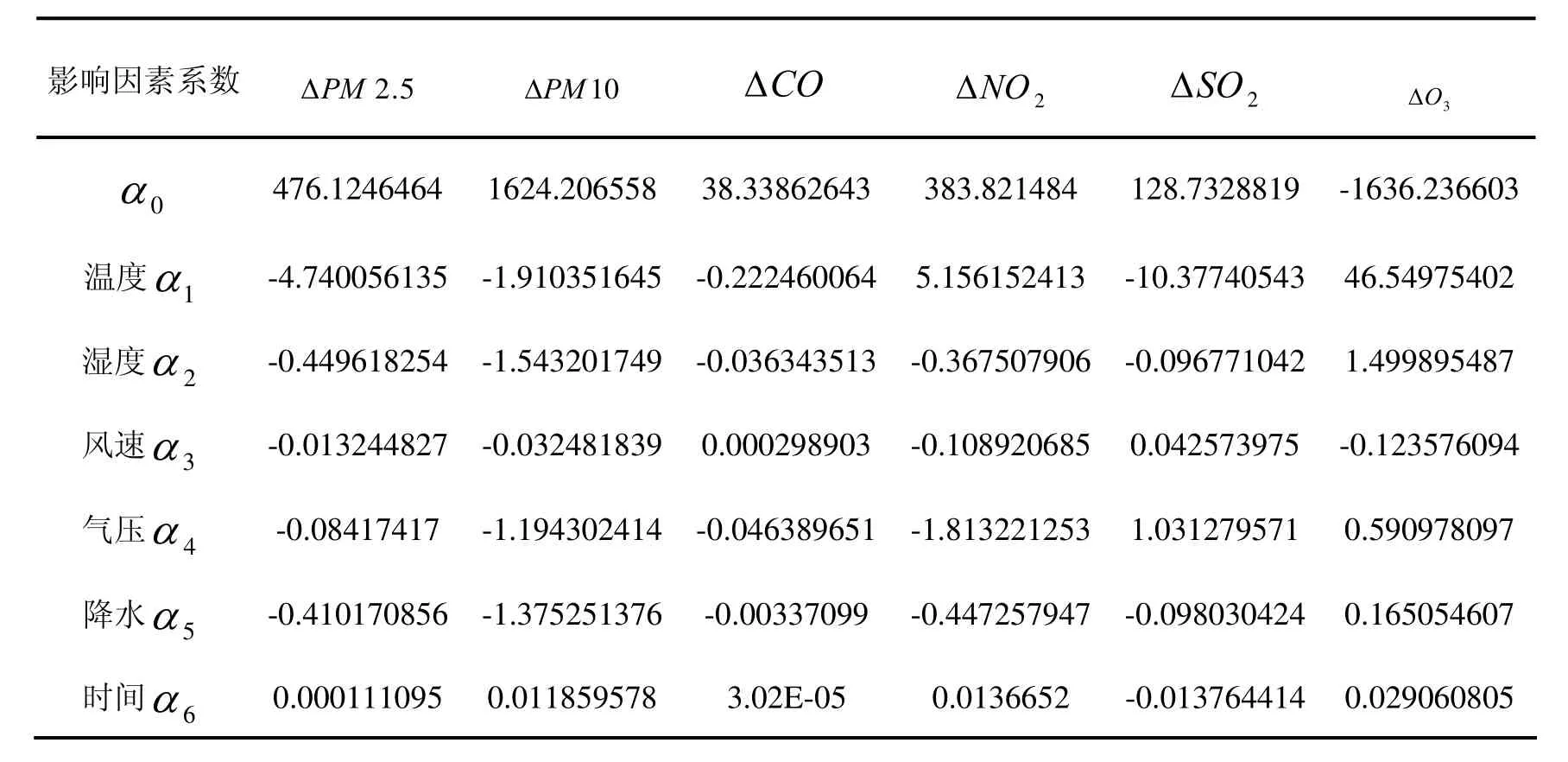
影響因素系數PM2.5 Δ ΔPM10 ΔCO NO2 ΔSO2 Δ 3 ΔO 0α 476.1246464 1624.206558 38.33862643 383.821484 128.7328819 -1636.236603溫度1α -4.740056135 -1.910351645-0.222460064 5.156152413-10.37740543 46.54975402濕度2α -0.449618254 -1.543201749-0.036343513-0.367507906-0.096771042 1.499895487風速3α -0.013244827 -0.032481839 0.000298903-0.108920685 0.042573975 -0.123576094氣壓4α -0.08417417 -1.194302414-0.046389651-1.813221253 1.031279571 0.590978097降水5α -0.410170856 -1.375251376-0.00337099-0.447257947-0.098030424 0.165054607時間6α 0.000111095 0.011859578 3.02E-05 0.0136652 -0.013764414 0.029060805

決定變量 Δ PM2.5 ΔPM10 ΔCO Δ NO2 Δ SO2 ΔO3 R2 0.3588 0.4859 0.1648 0.4288 0.5355 0.5372

從上表中看出，各個決定變量的R2普遍較小，最大的是0.5372，而ΔCO的R2只有0.1648，擬合度較低。因此，我們通過置信區間的范圍進行數據的重新篩選和匹配，以新數據為參照重新建立多元線性方程，得到新的回歸系數和相應R2如下表：

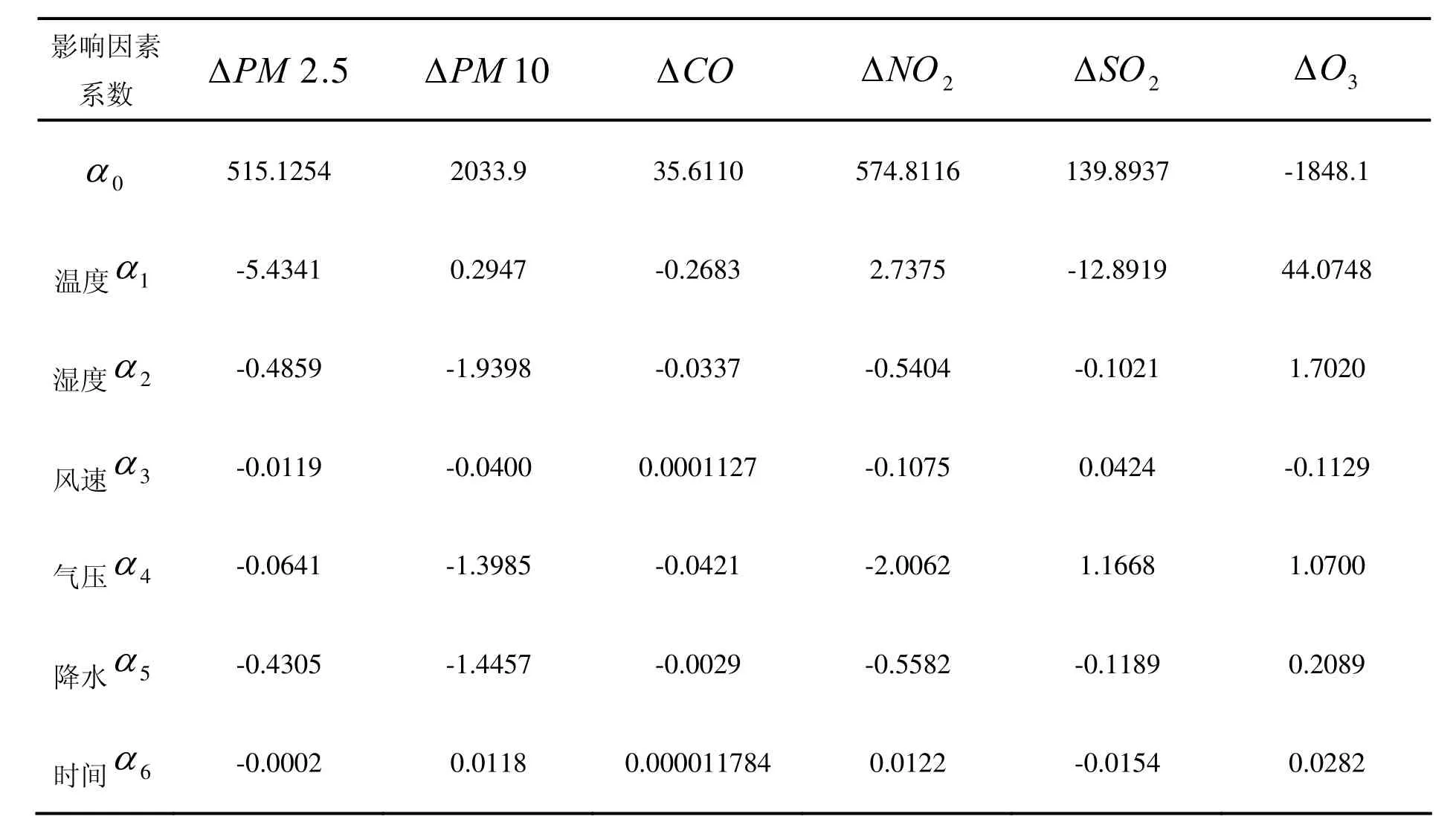
影響系因 數素ΔPM2.5 ΔPM10 ΔCO Δ NO2ΔSO2 ΔO3 α0 515.1254 2033.9 35.6110 574.8116 139.8937 -1848.1溫度α1 -5.4341 0.2947 -0.2683 2.7375 -12.8919 44.0748濕度α2 -0.4859 -1.9398 -0.0337 -0.5404 -0.1021 1.7020風速α3 -0.0119 -0.0400 0.0001127 -0.1075 0.0424 -0.1129氣壓α4 -0.0641 -1.3985 -0.0421 -2.0062 1.1668 1.0700降水α5 -0.4305 -1.4457 -0.0029 -0.5582 -0.1189 0.2089時間α6 -0.0002 0.0118 0.000011784 0.0122 -0.0154 0.0282

決定變量R2如下表：

決定變量ΔPM2.5Δ PM10ΔCO Δ NO2ΔSO2ΔO3 R20.477499875 0.649229706 0.219276757 0.541136841 0.541296013 0.650687979

從表里可以看出，各個決定變量的R2均有所增加，但是很多都在0.5附近，ΔCO的R2只有0.22，擬合效果仍不明顯。為此建立關于ΔPM2.5、ΔPM10、ΔCO、ΔNO2、ΔSO2、ΔO3的二次回歸方程，以ΔPM2.5為例：

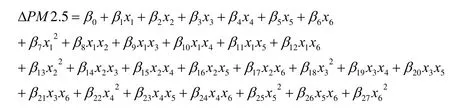
由于ΔSO2有6個異常點，重新匹配后，通過Matlab軟件運行得到回歸方程如下：

相應決定變量R2如下表：

從上表可以看出，各個決策變量的R2均大幅度增加，其中ΔSO2的R2最大達到0.7083，最小的ΔCO也達到了0.491，結果較為理想。在多元二次回歸方程下得到關于ΔPM2.5、ΔPM10、ΔCO、ΔNO2、ΔSO2、ΔO3的殘差圖,(這里只給出ΔPM2.5和ΔPM10的相關圖像)如下：

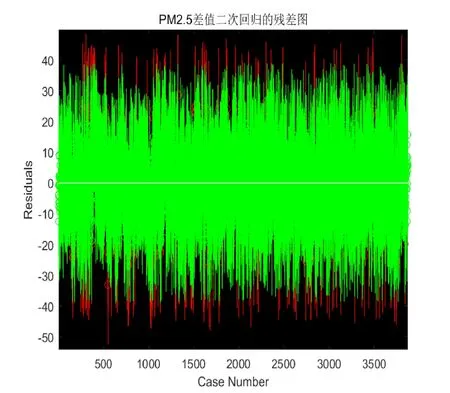
由殘差圖圖像，考慮到影響影響因素的不確定性，多元二次回歸模型的擬合效果較好。