柯西不等式的應用透視
2020-04-13 07:38:06山東劉美亭
高中數理化 2020年5期
◇ 山東 王 敏 劉美亭
1 求值



2 求最值







3 證明不等式
利用柯西不等式證明某些不等式特別方便,利用柯西不等式的技巧也有很多,如添項、配湊常數式、改變結構等.
3.1 添項

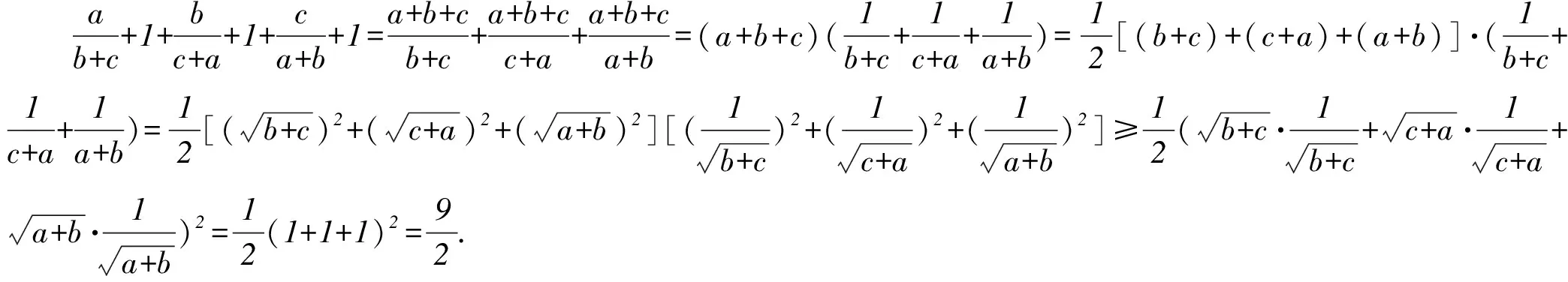
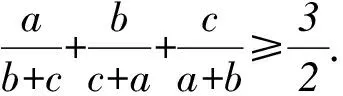

3.2 “1”的代換

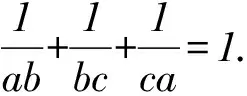
由柯西不等式,得
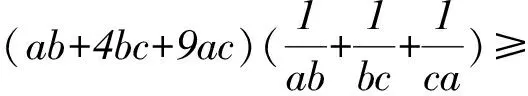
所以ab+4bc+9ac≥36,當且僅當a=2,b=3,c=1時,等號成立.

3.3 湊配常數式

(1)解不等式f(x)≥4;
(2)記函數f(x)的最小值為m,若a,b,c均為正實數,且a+2b+3c=2m,證明:

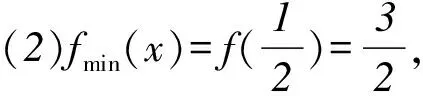
(a2+b2+c2)(12+22+32)≥(a+2b+3c)2,
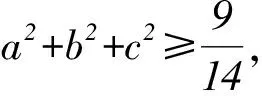

3.4 改變結構

證明由柯西不等式,得
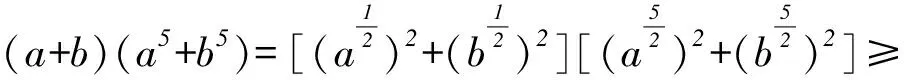
當且僅當a=b=1時,等號成立.
綜上,(a+b)(a5+b5)≥4.

4 求取值范圍

A.[-5,5] B.(-5,5)
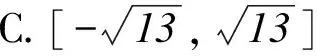

所以由柯西不等式
(32+22)[x2+(-x+y)2]≥
[3x+2(-x+y)]2=(3x-2x+2y)2=(x+2y)2,
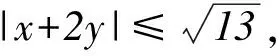



又由例8中的變式,得
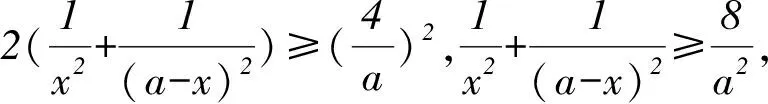
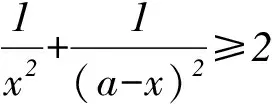

猜你喜歡
中等數學(2022年2期)2022-06-05 07:10:50
中學生數理化·七年級數學人教版(2021年11期)2021-12-06 05:38:48
哲學評論(2021年2期)2021-08-22 01:53:34
小學生學習指導(低年級)(2020年6期)2020-07-25 02:31:36
中華詩詞(2019年7期)2019-11-25 01:43:04
模具制造(2019年3期)2019-06-06 02:10:54
小學生學習指導(低年級)(2018年9期)2018-09-26 05:59:44
瘋狂英語·新讀寫(2018年2期)2018-09-07 09:32:10
數學小靈通·3-4年級(2017年6期)2017-06-22 11:28:50
影視與戲劇評論(2016年0期)2016-11-23 05:26:01

