一個和型不等式的定積分證明與思考
2020-04-13 07:38:12廣東孫傳平
高中數理化 2020年5期
◇ 廣東 孫傳平
1 題目

(1)若函數f(x)在x=0處有極值,求函數f(x)的最大值;
(2)是否存在實數b,使得關于x的不等式g(x)<0在(0,+∞)上恒成立?若存在,求出b的取值范圍;若不存在,說明理由;
本題前兩問比較容易,第(3)問有一定的難度.本文先給出第(3)問的定積分證法(此問證法不唯一,筆者認為定積分證法較為簡捷),再進行反思與拓展.
2 解法探究
證明(3)先證右邊,當n=1時,右邊不等式中等號成立;

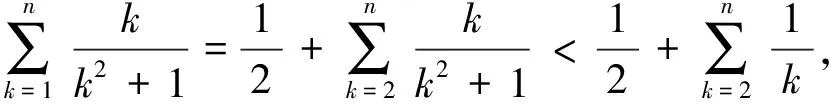
①
即
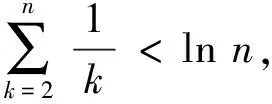
②
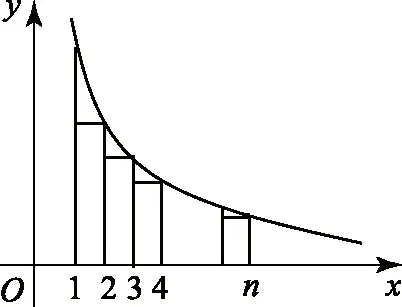
圖1
由①②,得
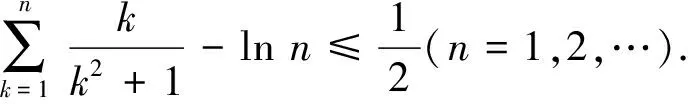
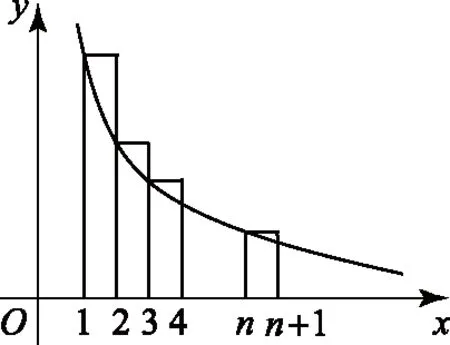
圖2
由區間[1,n+1]上的n個矩形的面積之和大于曲邊梯形的面積,得
即

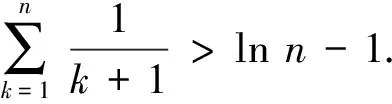
③
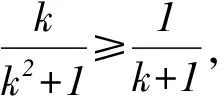
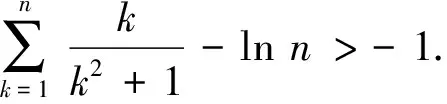
綜上所述,原不等式成立.
3 解后反思
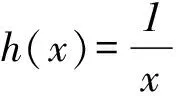
2)右邊不等式的證明過程中有一個步驟
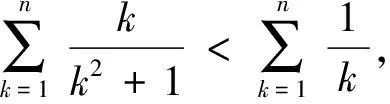
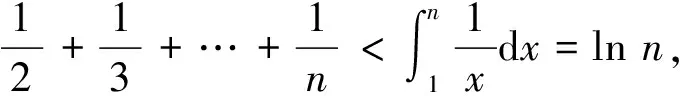
所以
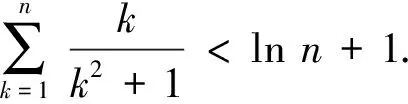
④
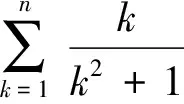
4 拓展
導數應用題中出現和型不等式的證明,并以此壓軸的現象在高考數學試題和各地模擬試題中正悄然升溫.

(1)用a表示出b,c;
(2)若f(x)≥lnx在[1,+∞)上恒成立,求a的取值范圍;

由S1>S2,問題易得證.
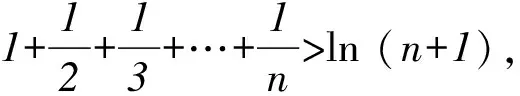
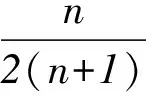
運用定積分證明和型不等式是高中數學課程中定積分應用的一大模塊,它思維起點低、思路清晰、操作簡便直觀,更難得的是它解決問題的普遍性.有關此類和型不等式的證明,一般都可以采用這一方法,因而成為我們破題的好幫手.此法甚好,不過要想做到駕輕就熟,還須注意:① 合理構建“理想函數”h(x)(必要時先放縮后構造);② 選準用于分割區間的圖形的形狀(矩形或梯形);③ 若有放縮法參與,還要注意控制放縮的“步伐”.

