也談小學數(shù)學游戲的開發(fā)與運用

楊軍

摘要：數(shù)學游戲的顯性表征是“游戲”，即有趣、有規(guī)則。有趣，能激發(fā)兒童的學習動機;有規(guī)則，就有競爭，兒童的智慧就會被“開啟”。隱性表征是“數(shù)學”，即具有較強的啟思性、探究性，能啟發(fā)兒童的數(shù)學思考和探究。可以說，數(shù)學游戲?qū)?shù)學的學習情趣和理性精神融為一體。在教學中開發(fā)與運用數(shù)學游戲的具體做法有：創(chuàng)新游戲設計，促學生產(chǎn)生認知興趣;強調(diào)游戲規(guī)則，讓學生享受挑戰(zhàn)樂趣;深化游戲體驗，使學生體悟思維理趣;注重游戲評價，引學生感受創(chuàng)造奇趣。

關鍵詞：數(shù)學游戲;設計;規(guī)則;體驗;評價

特級教師余穎在《數(shù)學小游戲——指向?qū)W生自由生長的教學新范式》一書中這樣定義“數(shù)學游戲”：“我們把一些蘊含數(shù)學道理，并且運用數(shù)學知識或者數(shù)學方法的智力游戲歸結(jié)為數(shù)學游戲。數(shù)學游戲不單純是游戲，也不是一般意義上的玩，它是將數(shù)學問題蘊含在游戲中，從而讓做游戲的人獲得數(shù)學活動的經(jīng)驗，潛移默化地掌握數(shù)學知識、思想與方法。”

數(shù)學游戲的顯性表征是“游戲”，即有趣、有規(guī)則。有趣，能激發(fā)兒童的學習動機;有規(guī)則，就有競爭，兒童的智慧就會被“開啟”。隱性表征是“數(shù)學”，即具有較強的啟思性、探究性，能啟發(fā)兒童的數(shù)學思考和探究。可以說，數(shù)學游戲?qū)?shù)學的學習情趣和理性精神融為一體。不少教師在教學中開發(fā)并運用數(shù)學游戲，從游戲設計到游戲評價，積累了一些實踐成果，筆者試做總結(jié)。

一、創(chuàng)新游戲設計，促學生產(chǎn)生認知興趣

為了促使學生產(chǎn)生濃厚的認知興趣，教師可基于教學內(nèi)容，創(chuàng)新游戲設計，巧妙地變學具為“玩具”。

例如，教學《圓錐的體積》一課，一位教師帶領學生“玩轉(zhuǎn)三角板”，游戲流程如下：

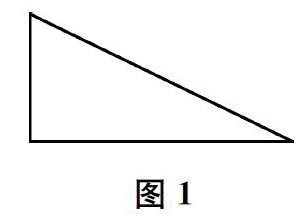
1.將一個直角三角板（如下頁圖1）以其中的任意一條直角邊為軸旋轉(zhuǎn)一周，旋轉(zhuǎn)后得到什么圖形？旋轉(zhuǎn)后的兩種圖形體積相同嗎？

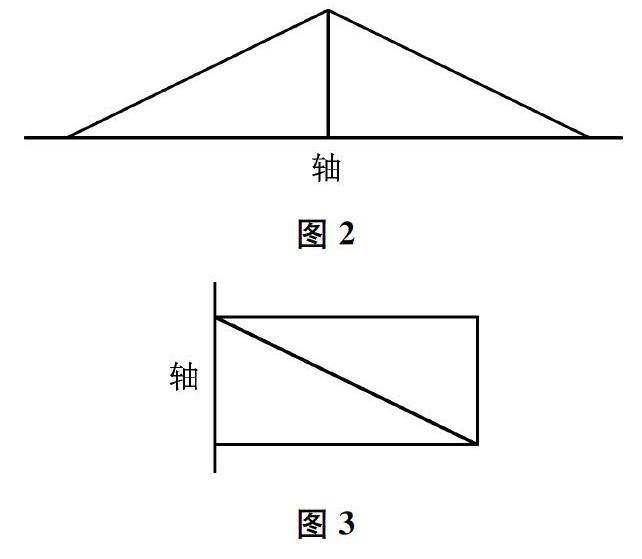
2.將兩個完全一樣的直角三角板拼成大三角形（如圖2）、長方形（如圖3），大三角形以最長邊為軸旋轉(zhuǎn)一周，長方形以寬為軸旋轉(zhuǎn)一周，求各自旋轉(zhuǎn)后所得圖形的體積。兩種拼法中每個三角板旋轉(zhuǎn)一周后所得圖形的體積相同嗎？

3.小組合作，將四個完全一樣的直角三角板拼成長方形（如圖4、圖5），分別以長為軸或?qū)挒檩S旋轉(zhuǎn)一周，每個三角板旋轉(zhuǎn)后所得圖形的體積是否相等？

熟悉的三角板，成了有趣的“玩具”，并且玩法多樣。游戲1中，同樣的三角板，以不同長度的直角邊為軸旋轉(zhuǎn)一周所得到的圖形的體積卻不相同。游戲2中，學生可以發(fā)揮想象，并發(fā)現(xiàn)趣味現(xiàn)象：圖2的拼法，兩個三角板旋轉(zhuǎn)后所得圖形的體積相同;圖3的拼法，兩個三角板旋轉(zhuǎn)后所得圖形的體積不相同。進一步辨析可知：圖3的拼法，每個三角板的面積是拼成的長方形面積的一半，而旋轉(zhuǎn)后各自形成的圖形的體積卻并不是整個圓柱體積的一半（一個是圓柱體積的三分之一，一個是圓柱體積的三分之二）。這與學生一開始的推測（受“面積相等”思維定式的影響，絕大部分學生認為體積也相等）明顯矛盾。游戲3中，學生在動手玩和想象中更深刻地認識到：圖4的四個三角板中，有兩對三角板旋轉(zhuǎn)后所得圖形的體積分別相同;圖5的四個三角板旋轉(zhuǎn)后所得圖形的體積均不相同（這與大部分學生的猜想明顯不一致）。

二、強調(diào)游戲規(guī)則，讓學生享受挑戰(zhàn)樂趣

游戲應遵循規(guī)則。在規(guī)則下進行公平、公正、公開的競爭，是游戲的靈魂。小學數(shù)學游戲規(guī)則可以是數(shù)學知識方面的要求，也可以是游戲競爭方面的要求。強調(diào)游戲規(guī)則，甚至巧妙變化游戲規(guī)則，往往可以促使學生積極探尋獲勝的策略，享受挑戰(zhàn)樂趣，展現(xiàn)思維活力。

例如，一位教師這樣帶領學生開展“搶數(shù)游戲”：

首先，教師出示“搶30”游戲規(guī)則：（1）從1開始，同桌兩人依次輪流報數(shù)，每人每次只能報1個數(shù)或2個數(shù)，不能多報，也不能不報;（2）誰先報到30，誰就獲勝;（3）猜拳，誰贏，誰先報數(shù)。為了幫助學生明晰游戲規(guī)則，教師安排了示范活動，讓學生對“從1開始”“依次輪流”“每次報數(shù)的個數(shù)”“猜拳決定先后”等要求有所感知。示范時，教師采取了讓自己贏的策略，讓學生感悟到游戲有一定的技巧，啟發(fā)學生思考：怎樣報數(shù)才能贏得比賽？在第一次游戲時，學生的反應是相對平淡的。但是隨著時間的推移，學生慢慢地熟悉了規(guī)則，開始謹慎地報數(shù)，競爭之心被激活，火藥味越來越濃。這是“游戲”的趣味性在向“數(shù)學”的探究性轉(zhuǎn)變。

接著，教師改變游戲規(guī)則：其余規(guī)則不變，誰先報到40，誰就獲勝。在適應規(guī)則變化的過程中，學生逐步明確獲勝秘訣：搶30，要搶到27、24、21……3，要后報數(shù);搶40，要搶到37、34、31……1，要先報數(shù);不管搶30還是搶40，都要三個一組地報，即對方報一個數(shù)，自己就報兩個數(shù)，對方報兩個數(shù)，自己就報一個數(shù)。游戲規(guī)則的微妙之變，使學生對“搶數(shù)游戲”中蘊含的3的倍數(shù)特征有了深刻的理解。

三、深化游戲體驗，使學生體悟思維理趣

很多數(shù)學游戲中蘊含著“大道理”，教師應當幫助學生深化游戲體驗，讓他們發(fā)現(xiàn)游戲中蘊含的數(shù)學知識、數(shù)學原理，體悟思維理趣。

例如，棋盤、棋子是學生常玩的游戲道具，很多學生會玩諸如五子棋等游戲。一位教師以它們?yōu)檩d體開展了“乘法原理”的教學：

教師首先出示游戲規(guī)則：（1）將A、B、C、D四顆不同的棋子放在4×4的方格棋盤中;（2）每行每列只能出現(xiàn)一顆棋子。在學生觀察之后提出問題：一共有多少種不同的放法？如果將A、B、C、D、E五顆不同的棋子放在5×5的方格棋盤中，有多少種不同的放法？將6顆棋子放到6×6的方格棋盤中呢？……學生嘗試擺放后展開思考：第一步放棋子A，A可以放在16個方格中的任意一個，所以有16種不同的放法;第二步放棋子B，由于A已經(jīng)放好，放A的這一行和這一列不能放B，問題轉(zhuǎn)化為在其余9格中放置B;第三步轉(zhuǎn)化為在4格中放置C;最后在僅剩的1格中放置D;得到（4×4）×（3×3）×（2×2）種放法。同理，得到5顆、6顆棋子的放法種數(shù)。此時，學生對乘法原理已經(jīng)有了初步的感悟。順著學生的思路，教師進行了深化：如果將n顆不同的棋子放在n×n的方格棋盤中，一共有多少種不同的放法呢？學生的思維也隨著游戲體驗更加深化，他們不再進行實踐操作，而是進行數(shù)學想象、推理，并發(fā)現(xiàn)可能的放法有（n×n）×[（n-1）×（n-1）]×…×（2×2）種，順利完成了知識的建構。

四、注重游戲評價，引學生感受創(chuàng)造奇趣

在游戲教學中，評價也不可或缺。教師要充分運用多元化的評價手段，激勵學生在開放性的游戲中拓寬解決問題的思路，發(fā)散想象，感受創(chuàng)造奇趣。

例如，在復習“圓的周長”時，一位教師創(chuàng)設了“滾圓”系列游戲任務，并展開了如下教學：

首先，教師出示初級“滾圓”任務：在一個邊長為12厘米的正方形內(nèi)部，將一張半徑為2厘米的圓形紙片沿著它的邊滾動一周。同時拋出問題：在滾動過程中，圓心經(jīng)過了多少厘米？大部分學生通過觀察發(fā)現(xiàn)，沿著正方形內(nèi)部滾動一周，圓心經(jīng)過的路線是一個正方形（如圖6），比較快捷地求出了圓心經(jīng)過路線的長度。教師給予學生最基本的“一星”評價，讓大部分學生受到激勵;并進行提升式點評：當圓片滾到頂點內(nèi)側(cè)位置時，圓心正好位于路線正方形的一個頂點。

接著，教師出示中級“滾圓”任務：將一張半徑為2厘米的圓形紙片沿著一個邊長為12厘米的正方形外圍滾動一周。由于內(nèi)部滾動的思維定式，對于外圍滾動，大部分學生不假思索，認為圓心經(jīng)過的路線也是正方形。教師適時對學生的操作、思路展開評價：真的是正方形嗎？它的4個“頂點”有特別之處嗎？并借助多媒體慢鏡頭播放滾動過程。學生恍然大悟：“滾”過正方形4個頂點的路線為圓弧，長度為圓周長的四分之一（如圖7），4個四分之一圓正好是一個整圓，所以滾動一圈，圓心經(jīng)過路線的長度為正方形的周長加上圓的周長。教師給予學生“二星”評價，以鼓勵學生的進階。

最后，教師出示終極“滾圓”任務：將一張半徑為2厘米的圓形紙片沿著圖8所示的不規(guī)則圖形外圍滾動一周。這一游戲更具挑戰(zhàn)性，有的學生認為，圓心經(jīng)過路線的長度等于這個圖形的周長;有的學生認為，就是這個圖形的周長加上圓的周長……教師再次借助多媒體進行點撥：這個游戲與前面兩個游戲有什么不同點和相同點？當圓形紙片滾動經(jīng)過哪幾個頂點時，圓心經(jīng)過路線的長度是圓周長的四分之一？在經(jīng)過哪些位置時，不具備這幾個頂點類似的特性？……經(jīng)過教師的點撥，學生想到了思路：雖然是沿著圖形的外圍滾動，但仔細分析（輔以實際操作）圓形紙片滾動經(jīng)過6個頂點的情況，可發(fā)現(xiàn)有1個頂點相當于內(nèi)部滾動（如圖9），為“直角頂點”，其余5個頂點相當于外圍滾動，為“圓頂點”（即中級任務中的圓弧）。并由此放飛靈感：雖然圖形沒有標出各段

的長度，但“直角頂點”兩邊的線段可以平移到一起，得到類似圖7的圖形（少兩段2厘米的線段），進而算得總長度。教師表揚了學生的靈感，并給予完成挑戰(zhàn)的學生“三星”評價。

在完成難度逐漸遞增的游戲任務的過程中，教師十分注重對學生的評價：有激勵性的星級評價，有針對性的“糾錯”評價，有開放性的“創(chuàng)意”評價。多元化的評價，促發(fā)了學生的靈感，引領學生感受到了游戲活動、數(shù)學方法的創(chuàng)造奇趣。

本文系江蘇省2017年基礎教育前瞻性教學改革實驗項目“小學游戲課程的開發(fā)與實施”、江蘇省南通市教育科學“十三五”規(guī)劃立項課題“小學游戲課程的開發(fā)與實施研究”（編號：GH2016042）的階段性研究成果。

參考文獻：

[1] 余穎，提秀雷.數(shù)學小游戲——指向?qū)W生自由生長的教學新范式[M].南京：江蘇鳳凰教育出版社，2017.

[2] 馬云鵬，吳正憲.深度學習：走向核心素養(yǎng)（學科教學指南·小學數(shù)學）[M].北京：教育科學出版社，2019.

[3] 宋宇.數(shù)學思維與生活智慧[M].北京：中國和平出版社，2006.

[4] 劉焱.兒童游戲通論[M].北京：北京師范大學出版社，2004.