Maple軟件在重積分教學中的應用

趙江林，嚴 勇

（四川民族學院理工學院，四川 康定626001）

0 引言

數學分析是數學類專業的基礎骨干課程，數學分析的學習狀況直接關系到常微分方程、復變函數、實變函數等后續課程的進一步學習［1-2］。因此，數學分析是數學類專業教學過程的重中之重。另一方面，重積分是教學分析教學的一個難點，掌握重積分的定義和計算有助于提高學生的學習興趣和解決實際問題的能力，是數學分析教學不可或缺的部分。重積分教學的關鍵是重積分定義的建立和重積分的計算，與之密切相關的是由函數、方程確定的空間圖形.隨著符號計算軟件Maple的不斷發展和完善，越來越多的被引入到數學學科教學中作為革新教學和增強學生解決實際問題能力的方法和手段，起到事半功倍的效果，能夠顯著的提高學生對抽象概念的動態理解［3-8］。在此基礎上，我們引入 Maple應用于數學分析中重積分的教學，彌補傳統黑板教學的不足，動態可視化重積分思想、積分區域，提高教學質量，改善教學效果，使課堂教學更加直觀、生動和全面。下面，我們將從模擬二重積分思想、繪制復雜積分相關區域圖形、計算簡單重積分三個方面來刻畫Maple軟件在重積分教學中的應用。本文所提到Maple均指Maple2016，所有Maple代碼均在Maple2016環境下運行。

1 積分思想的動態模擬

二重積分定義中涉及到“分割、近似、求和、取極限”重要數學思想，在傳統教學中，靜態的圖像很難展示“割之彌細，所失彌少”.為了對“分割、近似、求和、取極限”有更深刻的認識和了解，并揭示這些思想潛在的內涵，我們通過Maple軟件編制程序來模擬二重積分的定義過程，以實現課堂教學的最佳體驗。來刻畫二重積分定義推導過程的數學思想。

首先，繪制函數f（x，y）＝1+sin x+sin y的空間曲面圖形（見圖1）和積分∫D∫（1+sin x+sin y）dxdy，D＝｛（x，y）｜0≤x≤π，0≤y≤π｝的幾何意義及以 f（x，y）為頂的曲頂柱體（見圖 2），其程序 Maple程序如下［3］：

＞restart：#清楚內存

＞with（plots）：#加載 plots工具包

＞func1：＝1+sin（x）+sin（y）：#定義函數 f（x，y）＝1+sin x+sin y

＞fig1a：＝plot3d（func1，x＝0..Pi，y＝0..Pi，style＝patchnogrid）；#繪制函數圖像

＞fig1b：＝plot3d（func1，x＝0..Pi，y＝0..Pi，style＝patchnogrid，filled＝true）；#繪制以 f（x，y）為頂的曲頂柱體

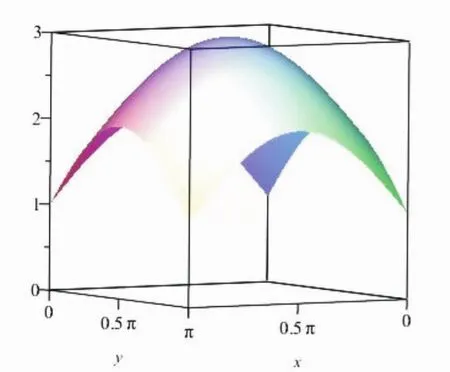
圖1 f（x，y）在D上的曲面圖

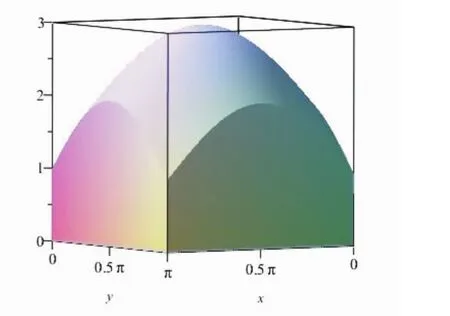
圖2 在D上，以f（x，y）為頂的曲頂柱體

為了刻畫“分割、近似、求和、取極限”重要數學思想，我們根基二重積分的幾何意義即曲頂柱體的體積，對 f（x，y）＝1+sin x+sin y在 D＝｛（x，y）｜0≤x≤π，0≤y≤π｝的二重積分的進行了動態演示（見圖3），其Maple程序如下：

＞restart：

＞with（plots）：with（plottools）：#加載 plots和 plottools工具包

＞func1：＝1+sin（x）+sin（y）：#定義函數 f（x，y）＝1+sin x+sin y

＞fig1a：＝plot3d（func1，x＝0..Pi，y＝0..Pi，style＝patchnogrid）：#繪制函數圖像

＞a：＝0：b：＝Pi：l：＝b-a：#定義常數

＞w：＝proc（n）#定義w函數

g：＝（i，j）-＞cuboid（［a+l*i/n，a+l*j/n，0］，［a+l*（i+1）/n，a+l*（j+1）/n，1+sin（a+l*（i+1）/n-（1/2）*l/n）+sin（a+l*（j+1）/n-（1/2）*l/n）］，color＝green）：#繪制單個小立方柱體

display（seq（seq（g（i，j），i＝0..n-1），j＝0..n-1））：#顯示所有的小立方體

＞p：＝animate（w，［n］，n＝1..50）：#動態顯示

＞display（p，fig1a）；#動態顯示逼近程度

從圖3中，當n＝1時，積分區域D沒有被分割，此時 “分割、近似、求和”體積與曲頂柱體的誤差最大；當n＝5，積分區域D被分割成25個小矩形，此時通過“分割、近似、求和”的體積與曲頂柱體的誤差縮小。隨著n（n＝15，25，35）的增大，我們能夠看到“分割、近似、求和”的體積與曲頂柱體的體積越來越接近。當n＝50時，積分區域D被分割成2500個小矩形，此時通過“分割、近似、求和”的體積與曲頂柱體的基本相同。

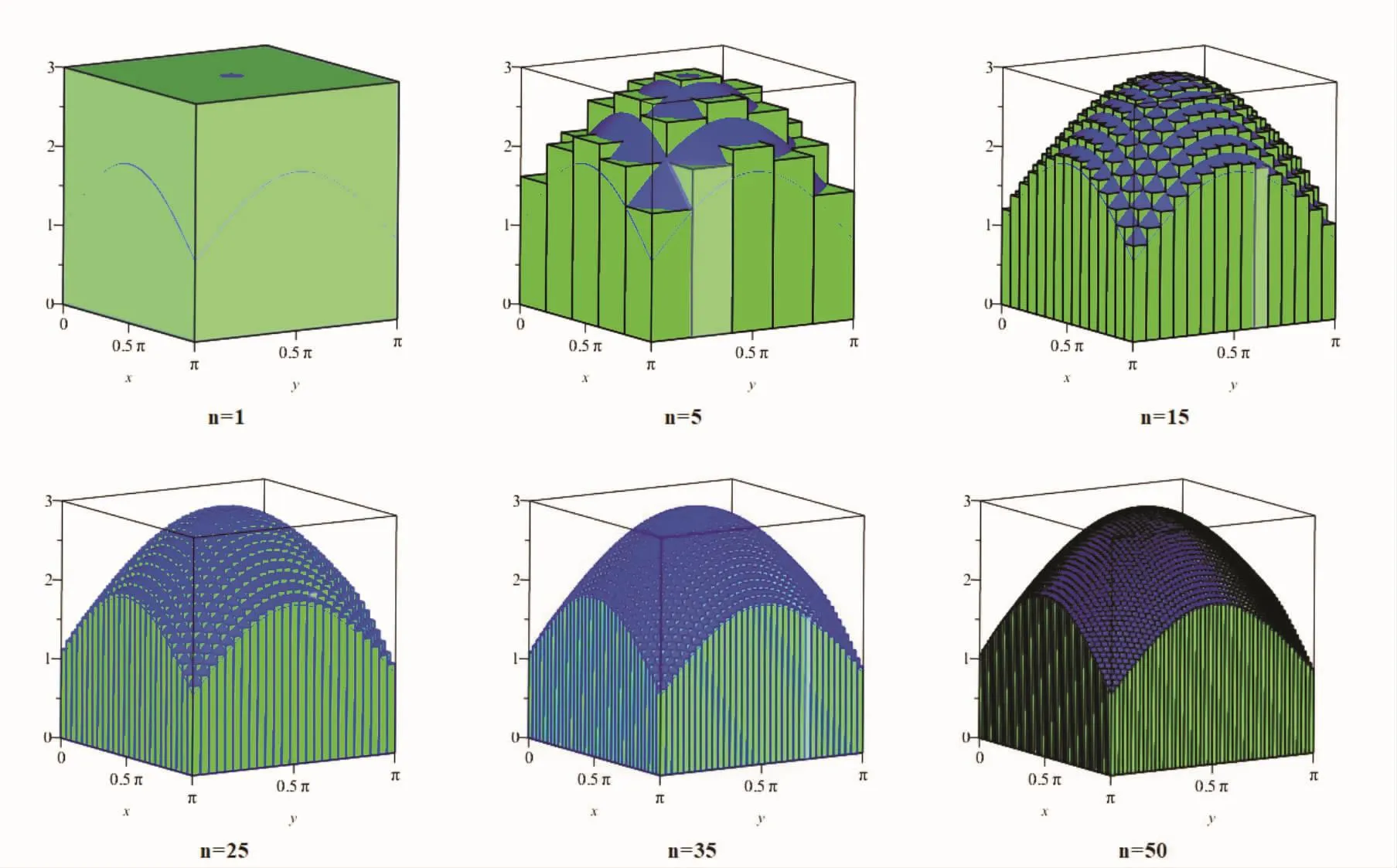
圖3 二重積分定義的展示

2 復雜區域的繪制

在求解二重積分或三重積分相關問題時，積分區域和被積函數的明確是解決問題的關鍵.下面我們用兩個例子說明。

例1.由z＝x2+3y2與z＝16-3x2-y2所圍成的立體的體積［5］。

根據被積函數為1的三重積分的幾何意義就是積分區域的體積，因此該問題的關鍵在于繪制出積分區域，其Maple程序如下：

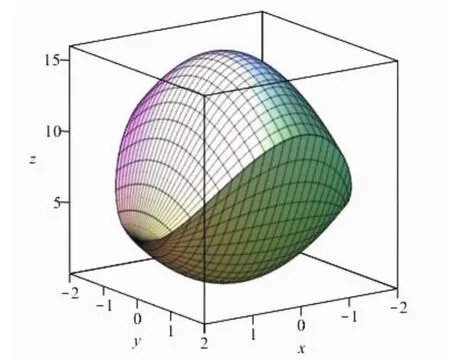
圖4 由z＝x2+3y2與z＝16-3x2-y2所圍成的空間圖形

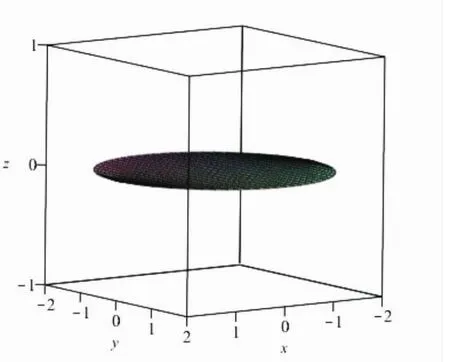
圖5 圖4在Oxy平面的投影

＞restart：

＞restart：

＞q1：＝plot3d（x＾2+3*y＾2，x＝ -2..2，y＝ -sqrt（-x＾2+4）..sqrt（-x＾2+4））：

政府補助是彌補市場失靈，引導產業資金流向，實現國家經濟目標和社會目標的重要手段。如Aihua Wu等 （2016）［4］研究認為政府補有助于企業獲得更多的銀行借款，且這種影響對于民營企業更加顯著。郭曉丹等 （2011）［5］研究了政府補助對于戰略性新興產業的信號效應，認為其對于企業產生了 “認證效應”和 “光環效應”，獲得了社會投資者的跟進。雷朋等 （2015）［6］采用了兩階段模型檢驗了政府補助對中國工業上市公司融資約束有顯著的緩和作用。

＞q2：＝plot3d（-3*x＾2-y＾2+16，x＝ -2..2，y＝ -sqrt（-x＾2+4）..sqrt（-x＾2+4））：

＞q：＝display（q1，q2）；

＞project（q，［［0，0，0］，［1，0，0］，［0，1，0］］）；

由圖4、圖5，我們能夠給出例1問題的積分區域：

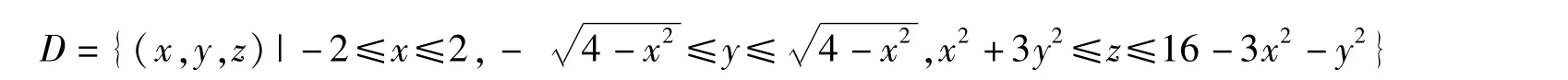
因此，例1問題等價于求解如下三重積分：

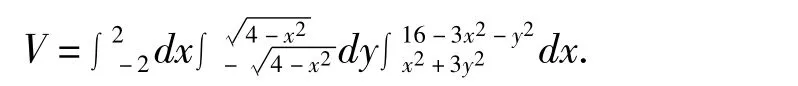
例2.在旋轉拋物面z＝x2+y2之下，Oxy平面z＝0之上，由圓柱面（x-1）2+y2＝1截出的空間立體體積［2］。

首先，我們繪制出該問題的立體圖形（見圖6），其Maple程序如下：

＞restart：

＞plot3d（x＾2+y＾2，x＝0..2，y＝ -sqrt（1-（x-1）＾2）..sqrt（1-（x-1）＾2），filled＝true，style＝patchnogrid）；

＞project（p，［［0，0，0］，［1，0，0］，［0，1，0］］）；

由圖7，我們能夠給出例2問題的積分區域：

D＝｛（x，y）｜（x-1）2+y2≤1｝.

因此，例2問題等價于求解如下二重積分：

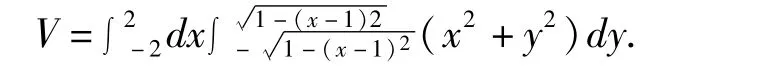
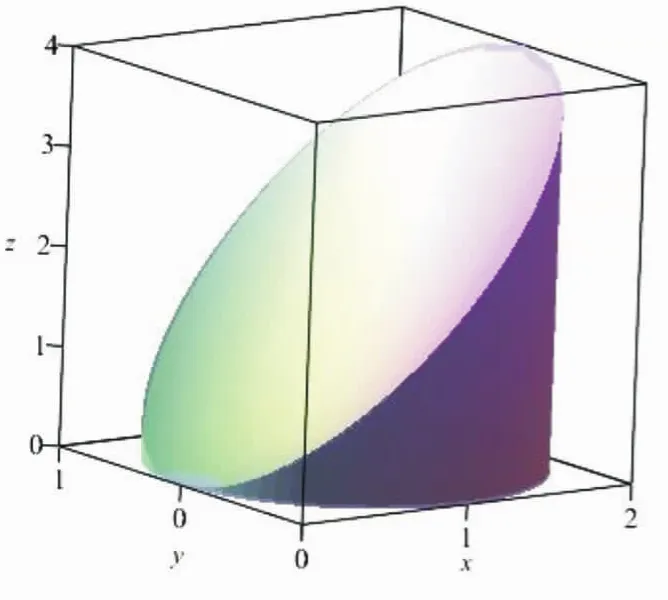
圖6 例2中的立體圖形

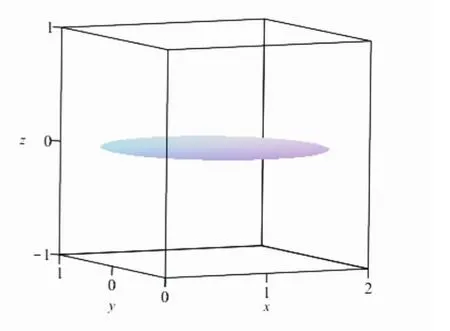
圖7 例2中立體圖形在Oxy平面的投影

3 計算簡單重積分

為了幫助學生學習二重積分的計算，使課堂教學更加高效，下面以計算

運行顯示：

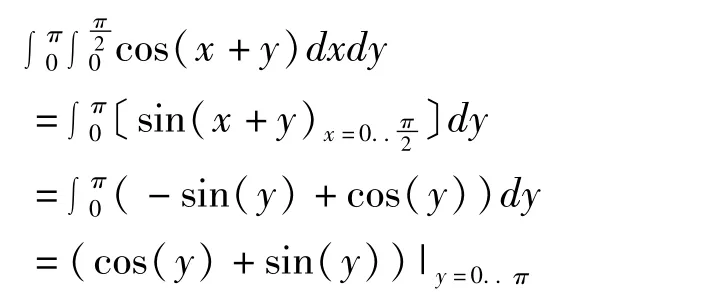
＝-2.

從上面例子可看出，該二重積分的計算步驟是清楚的，突破了數學解答過程中繁冗的計算量，這對于重積分課堂教學而言頗有效率，有利于我們專注于重積分計算的理論和技巧，提高課堂教學效果。

4 結論

在重積分教學中，掌握重積分的定義和重積分的計算是重積分教學的重點和難點。但是，重積分教學中繁瑣的計算往往使得教師講授和學生領會重積分定義和重積分計算的相關技巧有一定的難度。通過Maple模擬二重積分思想，我們在重積分教學中發現學生更容易掌握分割、取近似、求和、取極限的過程和更好地理解積分定義過程中的“以直代曲”思想。通過Maple繪制復雜積分區域和簡單重積分的演示，我們發現學生能夠更容易實現積分計算中的變量變換和積分區域的確定，提供積分的正確計算的前提，掌握變量替換技巧，從而提高了積分計算的正確性。更重要的是，我們在教學過程中實現了學生在能夠算的基礎上，讓學生體會了把具體問題求解抽象為數學模型的重要思想，為實現數學的應用和激發學生學習數學打下扎實的基礎。因此我們不難發現Maple軟件在重積分教學中能夠支持重積分的課堂教學，使教師講授時不僅能突出重點，凸顯關鍵，突破難點，實現重積分教學目標；而且能夠激發學生學習興趣，培養學生把實際問題抽象為數學模型并求解的能力。因此，在重積分的教學過程中Maple軟件的引入和使用有助于提高其教學質量和教學效果。