《概率論與數理統計》線上線下混合式教學實踐與創新研究

莊光明，梁文欽，郭寶英，趙國威，馬 琨，趙軍圣

（1.聊城大學數學科學學院，山東聊城252059；2.聊城市水城中學，山東 聊城252000；3.聊城市實驗中學，山東聊城252000）

0 引言

《概率論與數理統計》是研究、揭示隨機現象統計規律性的數學學科，在自然科學、社會科學、工程技術等諸多領域都有重要應用［1，2］。自從柯爾莫格洛夫（Kolmogorov）于1933年給出了隨機事件的概率P（A）的公理化定義，幾十年來，包括許寶騄在內的眾多國內外學者致力于概率論與數理統計學的研究，優秀成果不斷涌現［3-5］。然而，國內外現有的諸多研究成果語言比較專業化，不夠通俗易懂，而且主要注重的是理論推導，對問題的闡述和證明非常枯燥，使學習對象望而卻步，提不起深入學習的興趣。

在《概率論與數理統計》的長期課堂教學過程中，作者發現這門重要基礎課程的課堂教學往往存在著以下幾個方面的問題和窘境：

（1）缺乏實踐學習、自主學習和創新應用。《概率論與數理統計》是一門很注重實踐應用的學科，從最初的賭博和博弈、巴拿赫火柴盒問題、布豐投針實驗，到現在的正交試驗設計、金融數據分析、Monte Carlo隨機模擬等等，無不體現了實踐與應用［6-8］。然而，在現實的課堂上，教師和學生往往都缺乏對實踐與應用的重視，只關心考試，忽略了應用。這很大程度上導致了授課對象逐漸失去了對本課程深入學習的興趣，創新應用更加無從談起。

（2）重點知識點抓不住本質，不會學以致用。很多授課對象不能準確地闡述隨機事件的概率P（A）、制。隨機變量X等基本概念的本質和應用。很多同學不清楚引入隨機變量的目的，不能清晰地理解實際推斷原理，在學習假設檢驗時很難準確地給出拒絕域和接受域。諸如全概率公式、貝葉斯（Bayes）公式、大數定律，中心極限定理、假設檢驗、方差分析等重要知識點，很多授課對象沒有從根本上理解其本質和機理，只是為了考試死記硬背知識點，往往不能學以致用，非常迷茫和困惑。

（3）在課堂教學中不能深刻理解復雜概率問題的本質。在課堂教學中如果不借助現代多媒體技術，很難讓學生明白諸如多維聯合密度函數、邊際密度函數、條件密度函數等概念的本質。例如，學生很難深刻理解二維正態分布（Gauss分布）的密度函數：

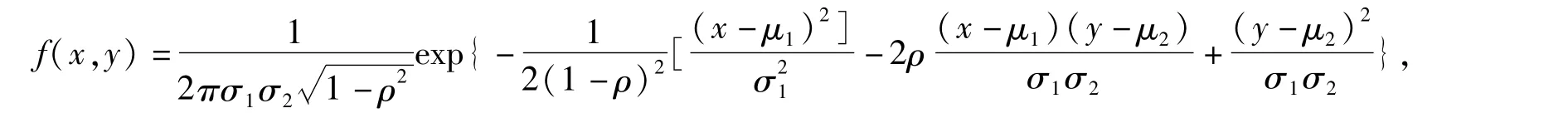
對其實際應用更是無法開展。

（4）由于對基本概念理解不夠深刻，不能舉一反三，大量的習題不會做，學生無力參加研究生考試和各類晉級考試。由于抓不住重要知識點的本質，授課對象只是簡單地死記硬背，結果導致大量的練習題不會做，期末考試勉強過關，害怕參加大型考試，沒有能力參加研究生考試和各類晉級考試。這種狀況嚴重制約了授課對象的自身發展和職業上升空間，也不利于個人工作能力的提升。

（5）學生不會操作相應的應用軟件，不會編程，埋沒了本學科自身廣泛的應用價值，制約了本學科服務社會的能力。SPSS、SAS、Eviews、Matlab等統計軟件可以很好地解決《概率論與數理統計》中遇到的實際問題，極大地減少計算工作量。但是，在實際的課堂教學中教師一般只講授知識點，授課對象對上述統計軟件了解甚少，當遇到處理大數據量的實際問題時無能為力，少數同學雖然知道用這些軟件，但缺乏對軟件的系統學習，對實際問題的處理也是無所適從。

1 本學科線上線下混合式教學闡釋

作為一種新興的教育形式，在線學習符合當今信息化社會網絡化的學習潮流，正在改變著實體課堂的傳統教學模式。在線學習中教師提供以教學課件、視頻為主要形式的學習資源，學生在線觀看課件、視頻，借助于網絡平臺進行師生間、生生間的交流互動，完成預設的在線測試作業、在線考試等［9-11］。這是對“課上教師講授+課下學生作業”的傳統課堂教學模式的補充和拓展，對學生的學習模式必將產生巨大的沖擊。

在線課程一般分為大型開放式和小規模限制性課程。MOOC（Massive Open Online Courses），即大型開放式在線課程［12-15］；SPOC（Small Private Online Courses），即小規模限制性在線課程［16-19］。混合式學習最早是指線上與線下的混合，即“E（Electronic Learning）+C（Classroom）”，當人們認識到單一的ELearning模式并不能取得滿意的效果時，開始考慮E-Learning與傳統教學的結合，通過實踐取得了很好的效果［12-20］。

《概率論與數理統計》作為研究隨機現象統計規律的數學學科，除要求學習者掌握基本知識點之外，還要求學習者學會對知識點深層次的探究和應用。實踐教學可以讓學習者深刻理解《概率論與數理統計》知識點的本質，強化訓練重點和難點。將《概率論與數理統計》實踐教學成果系統化后轉化為在線課程，教師要求學生通過網絡進行線上學習，線下回到學校的課堂上與老師、同學進行交互式學習，有利于學生對知識的深刻把握，節約課堂課時量，避免教師的滿堂灌而教學效果不佳的窘境，亟待得到加強。

因此，為了使得相關專業能夠達到對學生探索精神、科學思維、實踐能力、創新能力的培養要求，必須大力提升實踐教學理念，借助先進的在線學習方式，整合與優化線上線下混合式教學方式，更新課程內容，改進教學方法和技術手段，改革考試考核和成績評定方法。通過對本學科線上線下混合式教學模式的探索，促進學生對金融學、控制論、排隊論、信息論和決策論等交叉學科的初步認識和學習興趣，加強對新世紀高級應用型、創新型人才的培養［21-24］。

基于以上分析，非常有必要開展對《概率論與數理統計》線上線下混合式教學實踐與創新應用的研究。迄今為止，對本學科線上線下混合式教學實踐與創新應用的研究相對來說還比較薄弱，亟待加強和完善。

2 目標與方案

本著促進教學、服務社會的目的，圍繞實踐教學與創新應用這個中心，在積極推進實踐教學的基礎上逐步開展對線上線下混合式教學實踐與創新應用的研究。具體研究目標是：

（1）建立起完善的《概率論與數理統計》實踐教學大綱、實踐教學內容和課程標準，將實踐教學成果轉化為在線課程，突出線上線下混合式教學；

（2）依托在線學習平臺，建設《概率論與數理統計》在線教學課程，積極開展微課、慕課（MOOC）、SPOC及精品課程的建設；

（3）優化課堂教學，師生互動，注重應用，提高課堂效率，修訂教材，編寫相應的課件、習題集；

（4）基于應用型的課堂教學，通過實習支教、實驗教學、服務社會等手段強化實踐教學，促進課堂教學，逐步培養學生的實踐學習、自主學習和創新應用能力；

（5）探索線上線下混合式教學與創新應用的新思路，尋找師生互動、避免滿堂灌教學模式的新方法，提高課堂效率和應用能力，努力提升服務社會的能力。

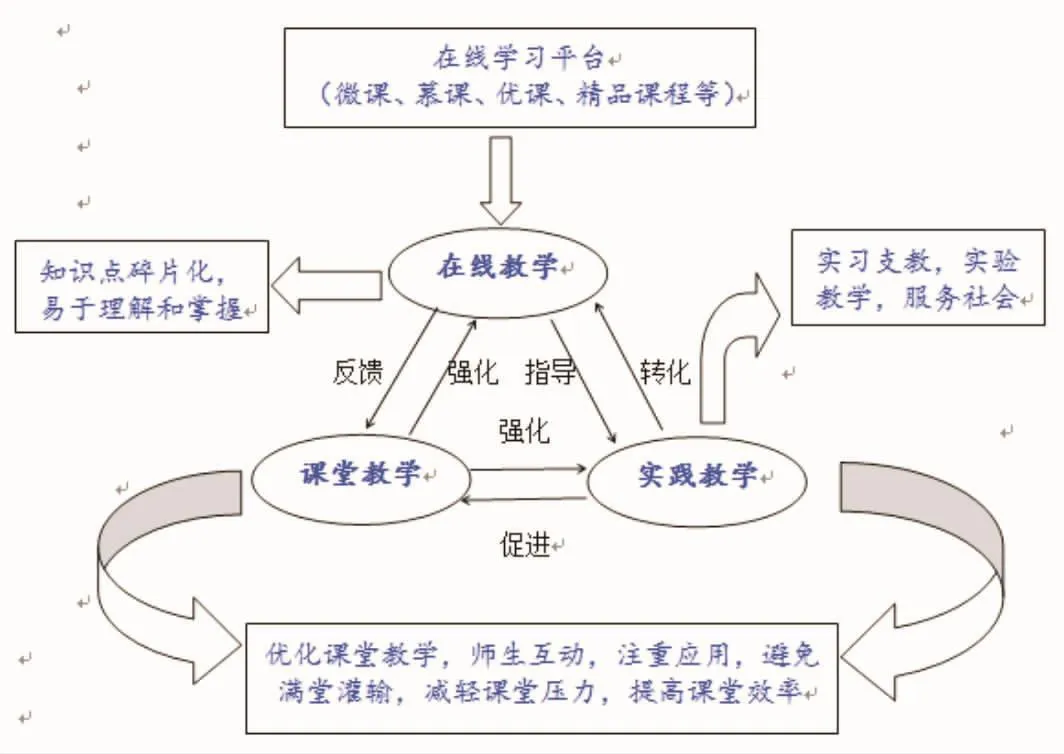
圖1 線上線下混合式教學研究方案

如圖1，研究方案總體思路：

（1）將重要的實踐教學知識點和教學內容轉化為微課和SPOC；

（2）加強課堂教學，側重知識點融匯貫通，強化練習應用，師生互動；

（3）根據SPOC反饋的情況，優化課堂教學和實踐教學；

（4）結合課堂教學和實踐教學，基于已有的微課和SPOC課程，適時開展MOOC建設，重點突出教學大綱中的重點和難點；

（5）將微課、SPOC、MOOC等在線課程教學情況反饋到課堂教學，進一步優化課堂教學，避免滿堂灌輸，減輕課堂壓力，提高課堂效率。

3 措施分析

（1）針對缺乏實踐創新的現象，在實踐教學中應注重理論聯系實際，積極挖掘課本知識的實踐應用。在針對貝葉斯（Bayes）公式的課堂教學中，作者引入了如下的實際問題：統計表明約80%的感冒由病毒引起，另有約20%的感冒由細菌引起。目前比較常用的判斷感冒類型的輔助手段是通過血常規檢查白細胞計數。醫學統計顯示，患細菌性感冒的人中70%白細胞計數增多，而病毒性感冒者白細胞計數增多的比例只有10%.如何判斷白細胞增多是由病毒性感冒還是細菌性感冒引起的呢？

令A＝｛患細菌性感冒｝，B＝｛白細胞計數增多｝，則由題意知

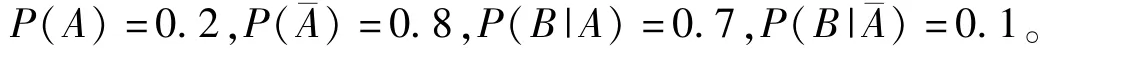
由貝葉斯（Bayes）公式，得

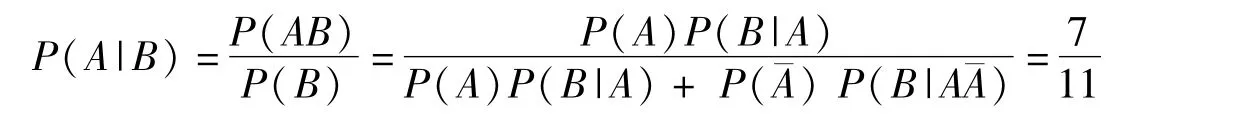
（2）很多同學不清楚引入隨機變量的目的：將隨機試驗的試驗結果數量化，通過分布函數作為橋梁，借助高等數學中函數、求和、積分等工具來研究復雜隨機事件的概率問題，完整地刻畫隨機變量的統計規律性。通過對比高等數學中單值函數f（x）的定義，可以清楚地闡述：

P（A）：滿足非負性、規范性、可列可加性的單值、實值的集合函數，

X（e）：定義在樣本空間S＝｛e｝上的單值、實值的集合函數，

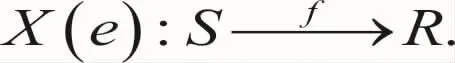
可見，P（A）、X（e）與高等數學中的單值實值函數f（x）本質上是一致的。

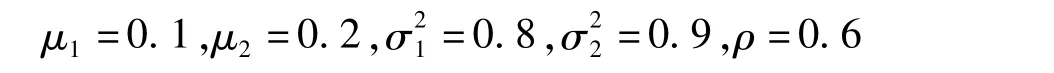
應用MATLAB軟件編寫程序，實現了一維正態、二維正態和條件概率密度函數圖像，如圖2-5所示。此時，

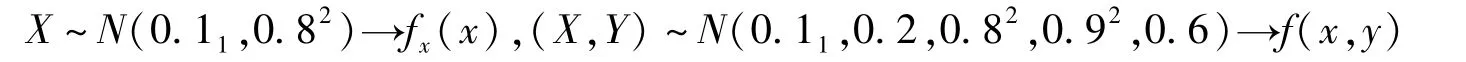
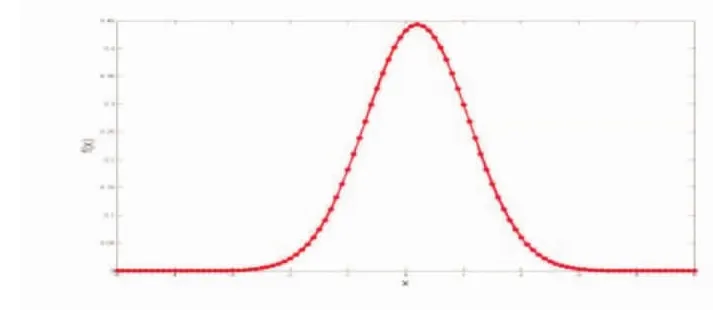
圖2 一維正態概率密度函數——鐘形曲線

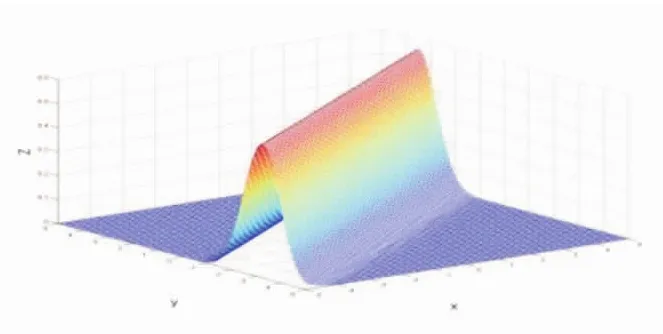
圖4ρ≠0時條件概率密度函數

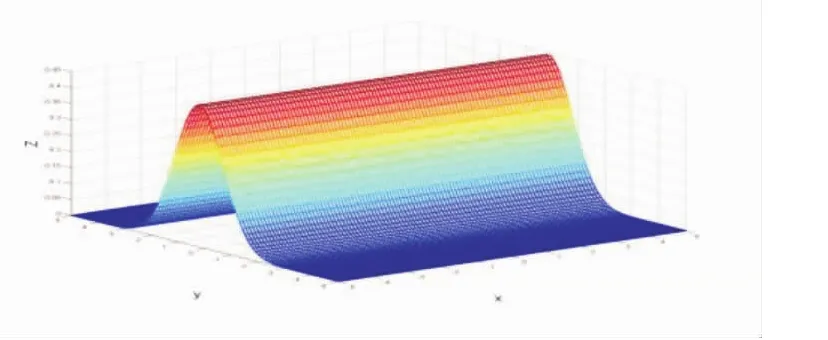
圖5ρ＝0時條件概率密度函數

在實踐教學中積極開展邊際密度函數、條件密度函數三維立體圖像的程序和軟件的研發，然后將這些實踐教學成果轉化為在線課程，展示出密度函數的三維立體剖面圖，學生會深刻理解多維密度函數和分布函數的概念及其重要應用價值，完成對聯合密度函數的二重積分，輕松計算如下復雜事件的概率：

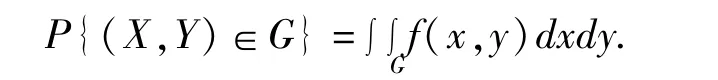
上述舉措不但可以促進課堂教學，而且可以逐步培養學生的實踐學習、自主學習和創新應用能力。

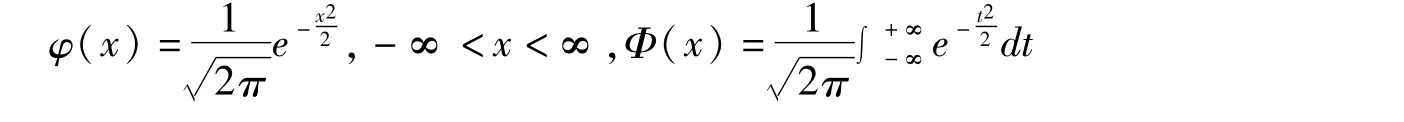
由正態分布的密度函數與分布函數的性質，結合圖6，易得Φ（+∞）＝1，

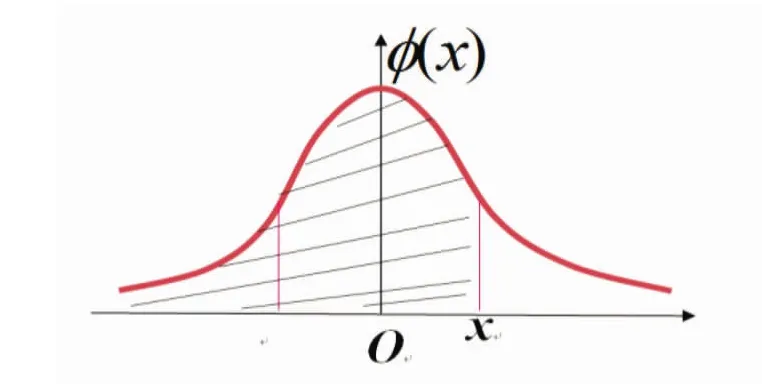
圖6 正態分布的密度函數與分布函數

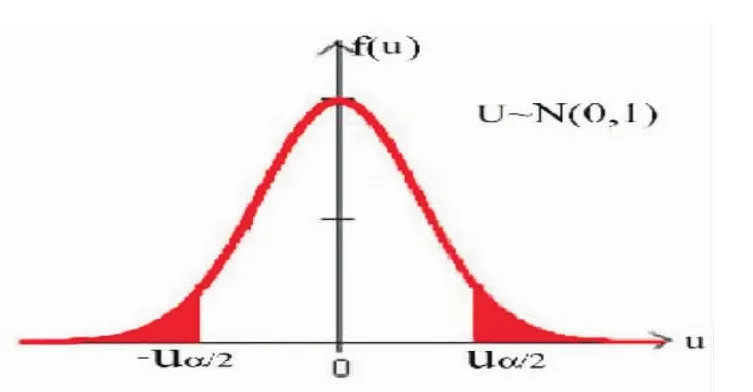
圖7 雙邊檢驗的拒絕域與接受域

從而避免了高等數學上用極坐標變換來得到上述積分的復雜計算。若計算∫，只要做變量代換，令t＝x-，則 dt＝dx，且有

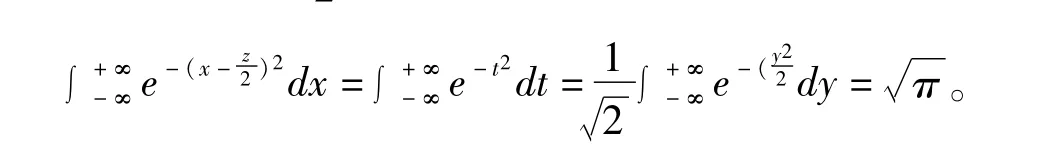
因此，只要根據標準正態分布中Φ（+∞）＝1的性質，上述積分問題迎刃而解。加強對標準正態分布密度函數φ（x）和分布函數Φ（x）的實踐教學，學習密度函數和分布函數的編程和仿真計算，具有明顯的實際意義。再將實踐教學成果轉化為在線課程，讓同學們隨時隨地方便地在線學習，必將促進課堂教學效果的提升。

（5）很多授課對象不理解實際推斷原理：小概率事件在一次實驗中不可能發生，而這正是顯著性假設檢驗的理論基礎，從而很難準確地給出假設檢驗的拒絕域和接受域。例如：設某廠生產的產品直徑服從正態分布N（26，5.22），現在抽取樣本容量為100的一個樣本，計算其樣本均值請問現在的生產是否正常？（設顯著性水平α＝0.05）.

由于總體分布的樣本方差已知，可以使用U檢驗法.根據題意，需要檢驗假設H0：μ＝26，H1：μ≠26，選用統計量，計算得

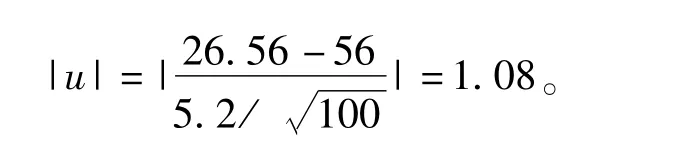
（6）在深刻理解事件概率、隨機變量、隨機過程等概念的基礎上，作者進行了正態分布、Brown運動（Wiener過程）、Markov過程等隨機過程的Matlab實現，完成了隨機系統的Monte carlo仿真與建模。我們探索了具有如圖8所示的3個模態的Markov跳變系統模態跳變程序的編寫。

不難看出，在實踐教學中通過對大量實際問題的仿真訓練，可以讓學生深刻理解重要知識點的本質和形成機理，而且在反復訓練中舉一反三，計算能力在實踐訓練中不斷被提升。再將這些實踐教學成果轉化為在線課程，將會極大地提高課堂教學水平和服務社會的能力。

圖8 Markov跳變系統模態

4 結束語

本文基于課堂教學中發現的若干棘手問題，詳細闡釋了《概率論與數理統計》線上線下混合式教學模式的研究意義、研究目標和研究方法，給出了具體、詳實的研究方案和執行措施。本文的中心舉措是將重要的實踐教學知識點和教學內容轉化為微課和SPOC，根據SPOC反饋的情況，優化課堂教學和實踐教學；結合課堂教學和實踐教學，基于已有的微課和SPOC課程，適時開展MOOC的建設；將微課、SPOC、MOOC等在線課程教學情況反饋到課堂教學，進一步優化課堂教學。本文將課堂教學、實踐教學和在線學習有機地融合為一體，凸顯了課堂教學成果、實踐教學成果轉化為在線課程的優勢及在線學習促進、優化課堂教學的能力。