車門結構多目標輕量化研究*

侯振方，胡海歐，張愛兵，李洪亮，霍俊焱

(1.寧波大學 機械工程與力學學院，浙江 寧波 315211；2.中國汽車技術研究中心有限公司，天津 300300)

0 引 言

作為汽車的重要組成部分，車門需要經常開啟與關閉。由于其位置的特殊性，在車輛發生側碰時，其對于駕駛員保護的重要性不言而喻。因此，車門的剛度與強度等關鍵性能就顯得極其重要；再者，降低整車的重量也是一種必然的趨勢。因此，在保證車身剛度、強度等性能不變差的前提下，對汽車的子系統進行輕量化研究具有重要的意義。

文獻[1]以車門垂向位移，一階彎曲頻率、一階扭轉頻率為約束，以車門質量為最小進行了單目標優化，最終在約束函數滿足條件的前提下，車門質量降低了0.72 kg；文獻[2]以汽車前端主要零部件厚度為優化變量，以擬合的Kriging模型近似替代了原有限元模型，以B柱加速度最大值最小為目標進行了碰撞優化設計，最終在滿足正目標的前提下，得到了一組最優的設計變量組合；文獻[3]將多目標響應問題的最優性與響應對可控因子波動的魯棒性問題聯系起來，同時考慮車門剛度以及碰撞等工況，對車門進行了基于穩健性的輕量化設計方法；文獻[4]利用網格變形技術創建了渦輪增壓器若干截面的形狀變量，通過擬合近似模型進行了多目標優化，最終得到了渦輪的體積與渦輪截面最大形變量之間的帕累托邊界；文獻[5]運用改進的遺傳算法對某型客車底架進行了多目標優化，輕量化效果非常好；文獻[6]模擬了電動客車4種極限工況，以各工況最大變形量以約束客車骨架質量為目標，最終骨架質量減輕了5.36%。但以上研究僅僅以板件的厚度或者形狀為單一變量進行優化設計，沒有同時考慮變量的尺寸與結構形狀可能對優化目標的影響。

本文基于車門多種工況，以板件厚度以及運用網格變形技術生成的形狀變量一同作為優化變量，同時考慮到車門一階固有頻率與車身扭轉頻率較為接近，以車門質量最小、一階頻率最大為目標，車門的窗框、垂向剛度為約束，嘗試運用混合設計變量對車門進行多目標輕量化設計。

1 車門有限元仿真與實驗分析

1.1 有限元模型分析

車門主要由厚度不同的鈑金件焊接而成，使用acm單元模擬點焊，螺栓通過剛性連接單元rbe2模擬，整個車門有限元模型共有47 685個單元，其中三角形單元2 033個，比例為4.4%，小于三角形單元占比。模型節點數為47 971，單元尺寸為8 mm×8 mm，車門原始總質量為20.89 kg，主要由21個厚度不同的板件組成，各個板件均采用shell單元進行網格劃分。

將建好的車門有限元模型施加各種工況并計算，可得出垂向剛度工況。作為車內與外界的通道，車門垂向剛度的好壞與其動態密封性能有直接關系。車門與車身安裝鉸鏈處的自由度全約束，并且在門鎖處約束第2個自由度(y向)，在門鎖孔的中心施加-Z(垂直向下)向大小為800 N的集中力，以加載集中力點的法向變形絕對值為評價指標。

其工況設置如圖1所示。

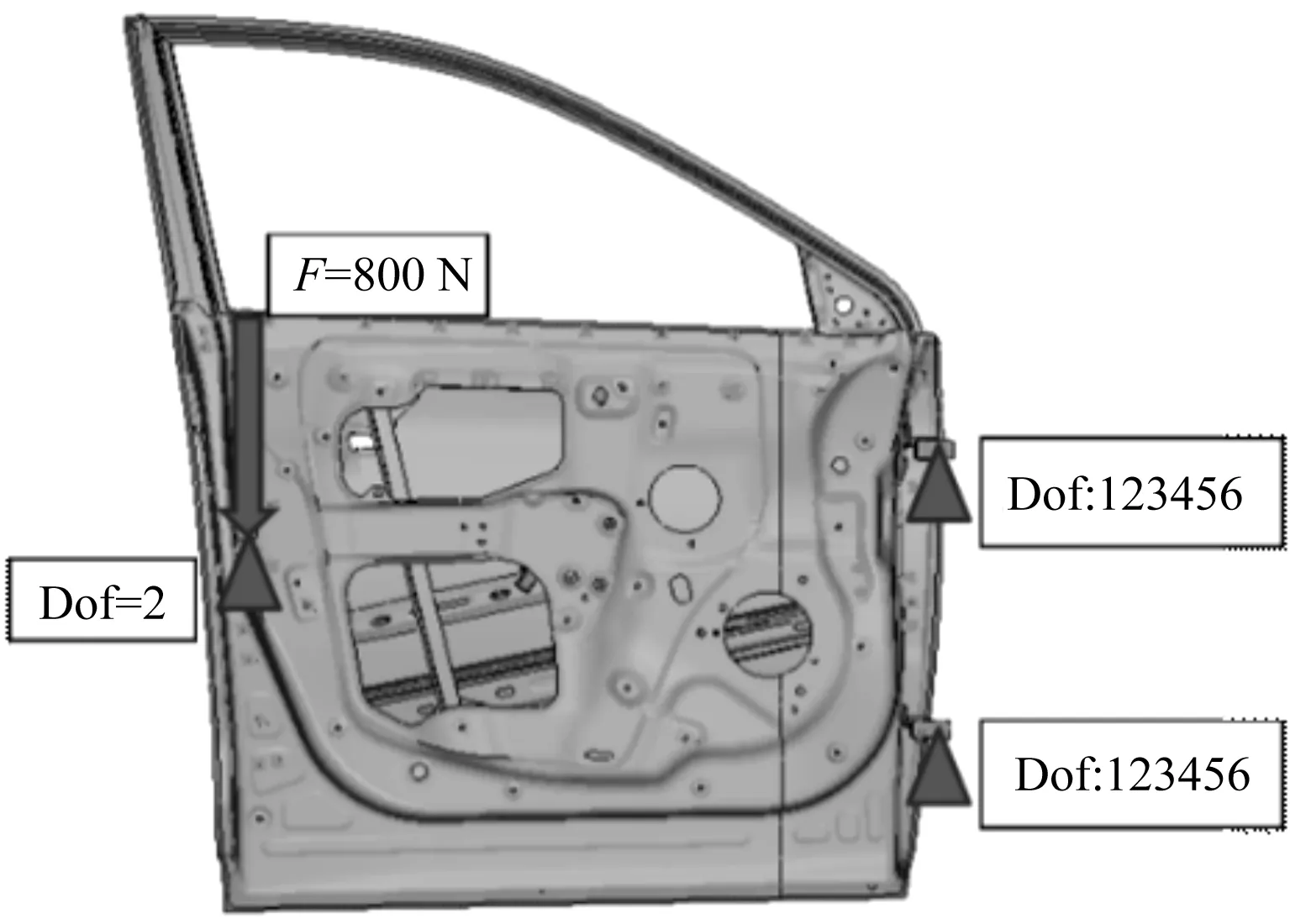
圖1 垂向剛度工況

窗框剛度工況：窗框剛度大小影響車門與車身之間的距離，因為局部結構的特殊性，窗框局部抵抗Y(垂直車門外板方向)方向變形的能力可以表征窗框剛度的大小，窗框部位的結構剛度如果過低，同樣影響其動態密封性能。

本文主要考察窗框角位置的局部剛度性能與車門鉸鏈處的自由度全約束，并且在門鎖處約束第4個自由度(繞x轉動)，在窗框局部處垂直面內施加F=200 N的集中力，以加載點法向變形量為評價標準。

具體工況設置如圖2所示。

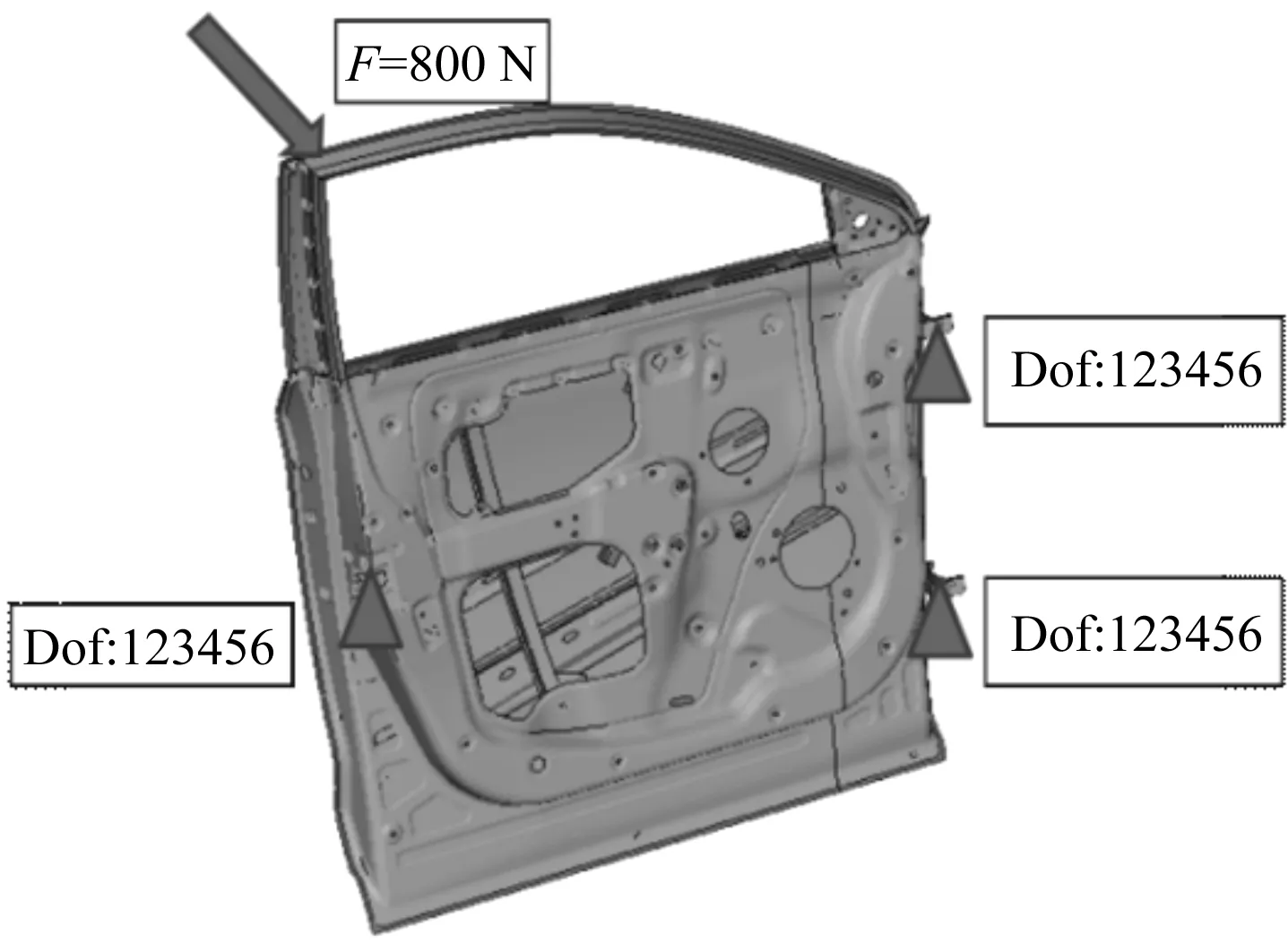
圖2 車門窗框工況

圖2中，分別用f、K1、K2、M表示一階頻率、垂向剛度、窗框剛度、質量。計算得出f、K1、K2、M的初始值分別為26.50 Hz、143.4 N/mm、43.5 N/mm、20.89 kg。

1.2 實驗及結果分析

筆者對該車門進行動態試驗(模態)測試，驗證有限元模型及其計算結果的可靠性，仿真模型計算工況與實驗保持一致。

車門的剛度實驗與模態試驗結果如表1所示。

表1 仿真與試驗結果對比

由表1可知：仿真分析中車門質量、垂向剛度、窗框剛度、一階模態與實驗結果的誤差均在5%以內，仿真與試驗結果誤差較小。因此，用有限元模型進行后續的分析計算是可行的。

2 定義形狀變量

目前常用的網格變形方式有4類：(1)morph volum；(2)map to geometry；(3)morph domains&handles；(4)freehand morphing。

第(1)種網格被包圍在3D塊里面，3D塊為變形體，用其邊界改變3D塊的形狀即可間接控制網格形狀；第(2)種為幾何映射，該方法對于模型的局部變形有很好的效果；第(3)種則更適用于模型的整體變形，該方法可通過控制全局或者局部手柄參數化地控制網格變形，可創建一些例如角度，圓弧等復雜的變形；第(4)種為網格自由變形方式，無需創建3D塊或者變形域等。

本文利用以上網格變形方式創建形狀變量，將車門板件厚度以及所創建的形狀變量作為設計變量。厚度變量有外板、腰線外加強板、外板支撐板、左內板、右內板、窗框三角板等。對網格或者節點進行移動、旋轉，可以改變截面的形狀，創建形狀變量；可對網格節點進行任意平移與旋轉獲得新的網格形狀。初始網格節點位置與變形后網格節點位置之間的位移矢量為形狀變量。

創建的4個形狀變量如圖3所示。

圖3 形狀變量示意圖1-右玻璃升降器截面；2-門把手區域；3-外板支撐板截面；4-防撞梁截面

3 基于混合變量的多目標優化

3.1 優化步驟

首先筆者進行優化目標以及約束的選定，然后進行DOE設計，生成空間樣本點，通過靈敏度分析篩選并去除對響應不敏感的一些變量，計算后提取目標與約束的值，最后以生成樣本點的變量和響應值作為輸入，構建近似模型，并確定優化算法，得出優化結果。

優化流程如圖4所示。

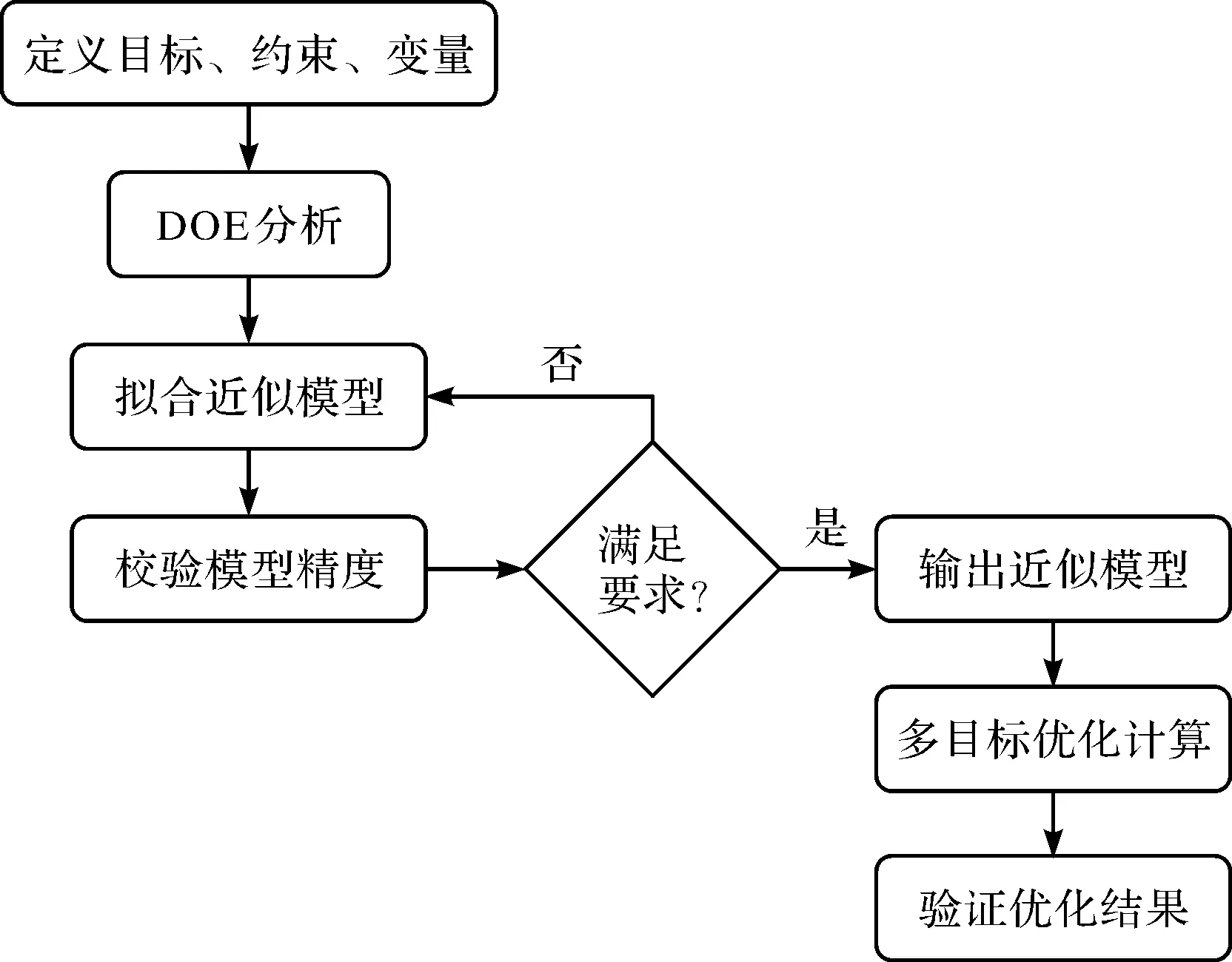
圖4 優化流程圖

3.2 Hammesley試驗設計

3.1節中生成樣本點數據的原因在于需要構建近似模型。所構建近似模型的精確度與樣本點在空間中的分布特征有很大的關系，樣本點選取的越多，分布越均勻，擬合近似模型的精度越高。本文利用Hammersley采樣法進行DOE，該方法可通過偽隨機數值發生器在超立方體中進行均勻抽樣。對比拉丁超立方抽樣方法，Hammersley采樣法能夠在K維超立方體中實現很好的均勻分布，而拉丁超立方只能在一維問題上有很好的均勻性[7]。

兩種采樣法在樣本點相同時的分布對比如圖5所示。

圖5 采樣分布對比1-拉丁超立方抽樣；2-Hammersley抽樣

由圖5可知：在樣本點相同時，Hammersley采樣法較拉丁超立方有更好的均勻性。樣本點確定的情況下，均勻性越好，近似模型精度就越高，因此選擇均勻性較好的Hammersley采樣進行實驗設計。

二維空間中的Hammersley點(xi,yi)可由下式產生：

xi=i/N

(1)

(2)

式中：0≤xi,yi≤1,i={0,1,…,N-1}；N—采樣點的總數目；k=log2N—不小于log2N的最小整數；[i/2j]—不大于i/2j的最大整數。

上式中共采用73組有效樣本點，將樣本點數據依次代入模型中，求得各工況的目標及約束值，得到的試驗設計矩陣如表2所示。

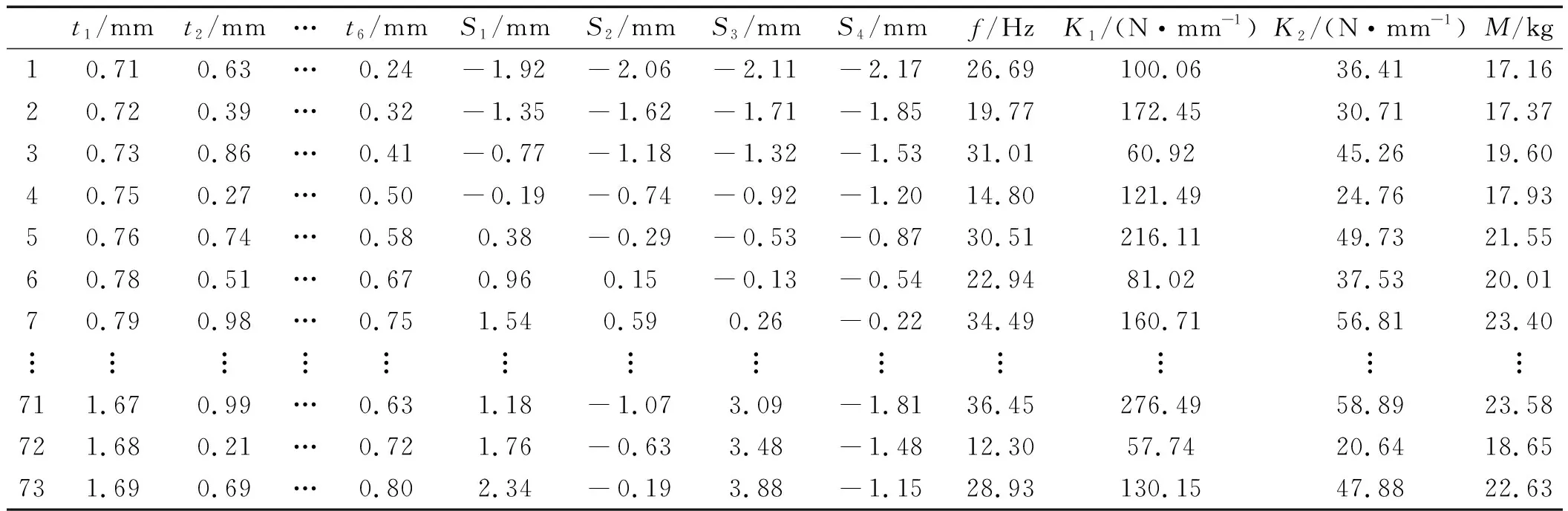
表2 基于Hamersley采樣的試驗矩陣

3.3 靈敏度分析

假設車門性能參數與設計變量函數關系式為Fn(t)，其中，n—性能參數的個數，t—設計變量；假如車門有3個需要優化的性能a、p、q，其表達式分別為Fa,Fp,Fq，定義為第i個設計變量；Fa,Fp與Fq和ti的相關性相反。假設定義：性能Fq的值最小，Fa、Fp為約束且有上限值，則ti對Fa的絕對靈敏度為：

(3)

同理，可得出Fp,Fq的ΔSp,ΔSq的值；ΔSaq為ti對Fa和Fq的相對靈敏度，定義為：

(4)

當|ΔSaq|<1時，對Fa的靈敏度小于對Fq的靈敏度；|ΔSaq|>1時，則反之；當|ΔSaq|=1時，ti對Fa的靈敏度等于對Fq的靈敏度，ti對Fp,Fq的相對靈敏度(同理可得ti對Fp,Fq的影響規律)為：

(5)

設計變量包括選取板件的厚度變量以及形狀變量，厚度變量分別用t1～t10表示，形狀變量分別用S1～S4表示，經以上靈敏度分析找出設計變量對每個響應的貢獻大小。

由設計變量對各響應的靈敏度分析結果得：對車門質量貢獻較大的有t6外板、t2左內板、t3右內板、t5腰線外加強板；對一階頻率貢獻較大的有t2左內板、t6外板、t3右內板、S2門把手區域；對垂向剛度貢獻較大的有t1窗框三角板、S1右玻璃升降器、S3外板支撐板、t6外板；對窗框剛度貢獻大的有t2左內板、t1窗框三角板、t6外板、t3右內板。

經分析，去除3個貢獻量小的厚度變量，共保留10個優化變量，其中，6個厚度變量為：t1窗框三角板、t2左內板、t3右內板、t4外板支撐板、t5腰線外加強板、t6外板；4個形狀變量為：S1右玻璃升降器截面、S2門把手區域、S3外板支撐板截面、S4防撞梁截面。

3.4 近似模型的擬合

由離散樣本組成的輸入與輸出信息可擬合近似數學模型。構建近似模型的好處在于可預測樣本點外輸入的響應，且與原有限元模型相比，近似模型計算速度要快很多。目前，實際中常用的近似數學模型有響應面模型、Kriging(克里格)模型以及RBF模型等。

Kriging模型是以設計變量的變異性與相關性為基礎，在設計變量空間內對其進行無偏、最佳估計[8]。由于該模型具有統計學特性的特點，噪聲信息對Kriging模型一般不會造成影響。該模型在其他建模方面也有較高的可信度[9-11]。Kriging模型以變異函數理論為基礎，可以不用建立像響應面法那樣明確的數學表達式。

從精確度以及計算效率考慮，本文利用克里格模型替代原有限元模型，以輸入變量和響應值為對應關系的Kriging模型可表示為：

Y(x)=f(x)+δ(x)

(6)

式中:Y(x)—擬合的Kriging模型；f(x)—樣本空間內的全局近似模型；δ(x)—局部偏差。

該偏差需要滿足的統計特性如下：

E(δ(x))=0

(7)

Var(δ(x))=σ2

(8)

Cov(δ(xi),δ(xj))=σ2RT(R(xi,xj))

(9)

式中：RT—沿對角線對稱的相關矩陣；R(xi,xj)—采樣點xi和xj之間的相關函數。

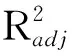
(10)

(11)

(12)

評價模型擬合精度的指標如表3所示。

表3 各工況Kriging近似模型的評價指標

由表3可知：用來評價所構建近似模型精度的決定系數以及調整決定系數值均接近1，MSE的值非常小。由此可見，可以用克里格模型替代原模型進行車門結構的輕量化設計求解。

3.5 多目標優化求解

本文以車門一階頻率最大和車門質量最小為目標，垂向剛度與窗框剛度為約束，具體定義如下：

(13)

式中：f—一階頻率；M—質量；K1—垂向剛度；K2—窗框剛度；t—厚度變量；s—形狀變量；tL—厚度上限；tU—厚度下限；SL—形狀變量上限；SU—形狀變量下限。

筆者以前面章節擬合的Kriging模型為基礎，運用多目標遺傳算法搜尋得出最優解集。優化時，因為所定義的目標會存在沖突的可能，最優解集中的某個解可能只在某個目標上是好的。這些在改進任何目標函數的同時，必然會削弱至少一個其他目標函數的解稱為非支配解或pareto解[13-15]。

筆者獲得pareto解集后,從最優解集中選擇3組最優解進行結果驗證，修改原始模型中板件厚度以及形狀變量的值，然后計算，結果與選取的最優結果對比，誤差均低于6%。

優化獲得的pareto前沿如圖6所示。

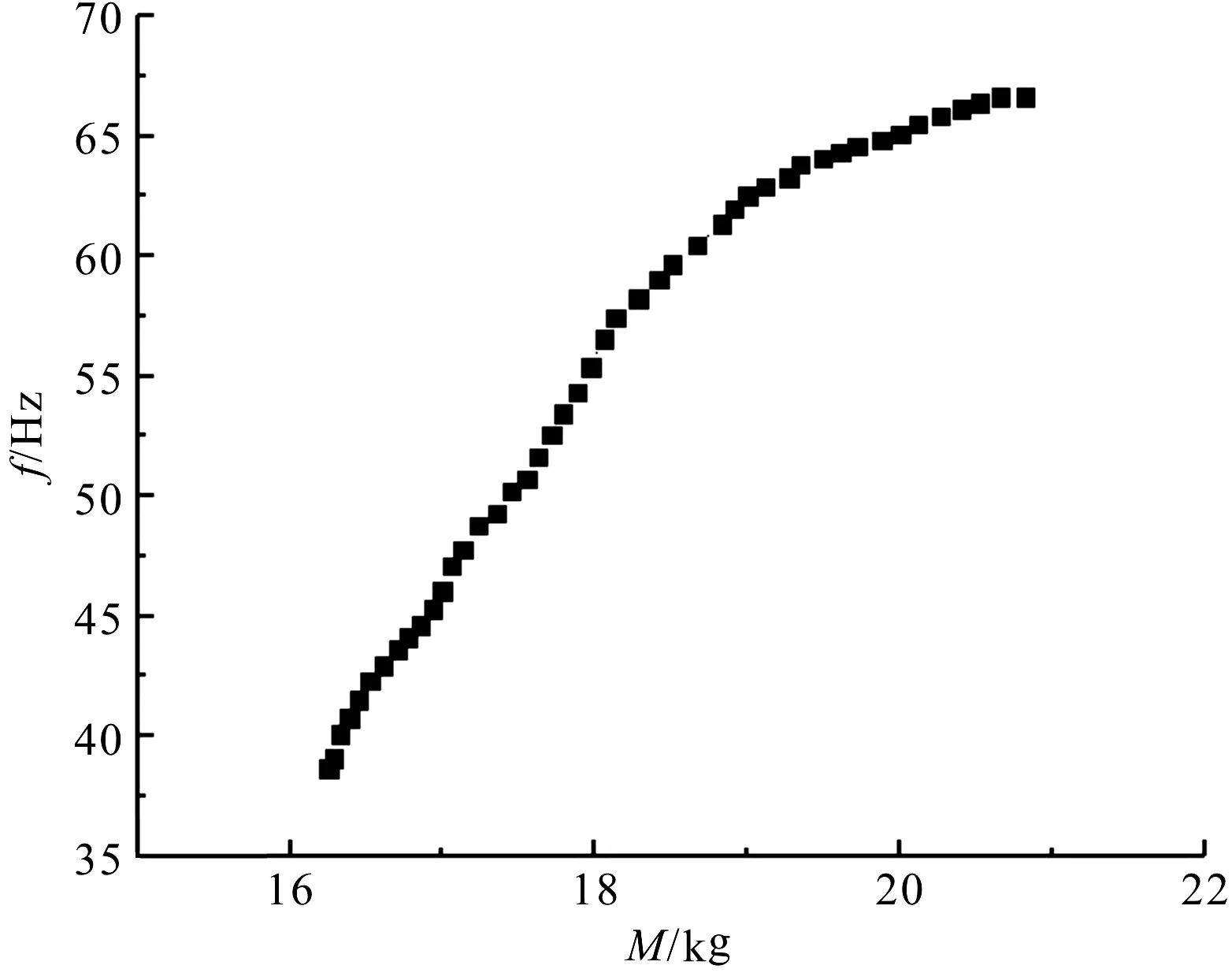
圖6 pareto最優前沿

由圖6可知：在車門窗框以及垂向剛度約束條件下，一階頻率最高可達67 Hz，車門質量最低為16 kg，輕量化效果較為明顯，同時一階頻率又能有較大的提升，從而有效避免了車門一階固有頻率與車身一階扭轉頻率耦合的可能性，因此得到的pareto優化解集較為理想。

綜合考慮選擇誤差最小的第3組為目標解，具體如表4所示。

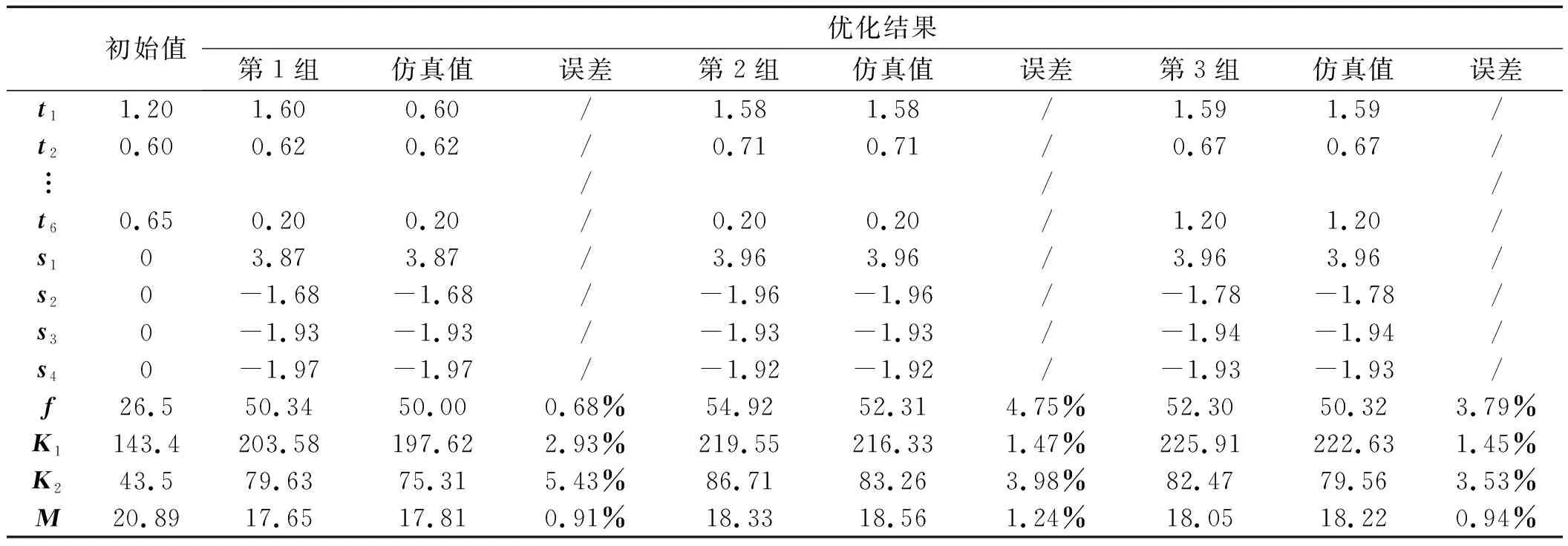
表4 優化結果及驗證

4 結束語

基于車門多種工況，筆者將厚度變量與運用網格變形技術生成的形狀變量一同作為設計變量，對車門進行多目標輕量化設計；

經過Hammersley采樣、試驗設計、靈敏度分析，擬合得到高精度的近似數學模型，結合NSGA算法，提高了優化迭代的效率，可以科學、高效地指導車門結構的優化過程；

同時考慮車門垂向剛度、窗框剛度以及一階模態等工況，對車門進行了多目標輕量化設計，得到了多目標優化的帕累托前沿解集。

研究結果表明：在車門垂向、窗框剛度達標的前提下，其質量降低2.84 kg(減重13%)，一階頻率提高25.8 Hz。

參考文獻(References):

[1] 朱紅軍,胡澤豪,李落星,等.基于Hyperstudy的車門結構多目標優化方法研究[J].制造業自動化，2015，37(24)：77-81.

[2] 王國春,成艾國,胡朝輝,等.基于Kriging模型的汽車前部結構的耐撞性優化[J].汽車工程,2011,33(3)：208-212.

[3] 王 棟,王麗娟,陳宗渝,等.穩健性和輕量化在車門結構優化設計中的應用[J].機械科學與技術，2019，38(4)：626-633.

[4] 劉孟祥,胡遼平,謝 輝.基于形狀變量和全局響應面法的增壓器渦輪多目標優化[J].內燃機程，2013，34(4)：71-76.

[5] 高云凱,段少東.基于NSGA-Ⅱ算法的客車底架的離散拓撲優化[J].同濟大學學報：自然科學版，2017，45(11)：1664-1669.

[6] 高 晉,艾田付,楊秀建,等.某電動客車車身骨架的輕量化[J].江蘇大學學報：自然科學版，2017,38(5):522-528.

[7] 周會峰,王光耀,李碧浩,等.多目標優化設計方法在車身輕量化設計中的應用[J].機械設計與研究，2014，30(4)：11-155.

[8] 朱茂桃,錢 洋,顧婭欣,等.基于Kriging模型的車門剛度和模態優化[J].汽車工程,2013,35(11):1047-1050.

[9] SONG S I，PARK G J. Multidisciplinary optimization of an automotive door with a tailored blank[J] .Automobile Enginering,2006 ,220(2),151-163.

[10] GU X, SUN G, LI G, et al. A comparative study onmulti-objective reliable and robust optimization forcrashworthiness design of vehicle structure[J]. Structuraland Multidisciplinary Optimization, 2013,48(3): 669-684.

[11] YOON T H, KIM H, HEO C, et al. An experiment and FEsimulation for the development of a SPFC1180 AHSS one-bodydoor impact beam about a car side collision[J].International Journal of Precision Engineering andManufacturing, 2016, 17(1): 81-89.

[12] 方柘林,王麗娟,陳宗渝,等.基于車門結構的多目標優化設計方法研究[J].機械設計,2014,31(8):60-64.

[13] 呂仲明,徐盛林，肉孜·阿木提.基于FLUENT的燒肉爐的優化設計及試驗分析[J].包裝與食品機械,2018(1):28-32.

[14] 曹巨江,楊奔奔,劉言松,等.高速取紙機構主凸輪廓線設計及其優化[J].包裝與食品機械,2019(4):29-33.

[15] 韓善靈,呂興棟,盧 翔,等.基于Hyperworks的電動汽車前艙蓋多目標形狀優化[J].現代制造工程，2018(5)：73-78.