Kr原子與CS分子相互作用勢及束縛態的理論研究

段 瑞, 錢 靜, 潘孝鳳, 朱 超, 李寬國, 鳳爾銀, 黃武英

(安徽師范大學物理與電子信息學院, 蕪湖 241000 )

1 引 言

隨著高分辨光譜技術的發展, 在毫米和紅外波長觀測分子輻射成為研究天體物質物理和化學條件的有力工具. 一氧化碳(CO)和一硫化碳(CS)分子均是星際云層中較為豐富的氣體, 它們在天體物理和天體化學中扮演著很重要的角色. 因此CO和CS分子與空氣中稀有氣體(Rg)組成的范德瓦爾斯體系引起了大家的廣泛關注. Rg (Rg = He, Ne, Ar, Kr)-CO復合物已經在實驗上和理論上[1-6]有了較為廣泛地研究, 而同族氣體CS分子和Rg原子間的弱相互作用(以下稱Rg-CS體系)近些年也逐漸開展起來.

2007年Lique等人利用振轉耦合無限階突變(VCC-IOS)方法計算了He-CS體系基態及振轉激發態能量, 給出該體系的極值位置在R=7.25a0,θ=105.0°, 其勢能值為-21.76 cm-1[7]. 同年, 他們對該體系的碰撞特性進行了深入地研究[8]. 2014年Chisato等人用傅里葉轉換微波光譜儀測定出Ar-CS 體系純轉動躍遷光譜, 并利用從頭算方法得到該體系的勢能面, 發現體系的全局極小值位于R=7.49a0,θ=109.3°, 其勢能值為-149.1 cm-1[9].

雖然He-CS和Ar-CS體系相互作用已有相關報道, 但是目前為止還未發現與Kr-CS體系光譜相關的實驗與理論報道. 為了得到Kr-CS體系較為精確的勢能面和微波譜數據, 為實驗提供可靠的理論依據, 本文采用CCSD(T)方法以及aug-cc-pVQZ基組(C、S原子)和aug-cc-pV5Z-pp (Kr原子) , 計算得到該體系的從頭算勢能面, 并通過數值求解Schr?dinger方程, 計算了體系的束縛態能級, 從而得到該體系的微波譜躍遷頻率.

2 計算方法

2.1 體系離散相互作用勢的計算及勢能面擬合

本文采用單雙迭代(包含非迭代三重激發)耦合簇理論CCSD(T)方法[10], 對C與S原子采用擴展相關一致基組aug-cc-pVQZ基組[11], 對Kr原子采用加入相對論效應的aug-cc-pV5Z-pp基組. 為了加速收斂, 在Kr原子與CS分子質心連線的中點處加入3s3p2d2f1g的鍵函數[12]. 在相互作用勢的計算中固定CS為平衡構型:re= 2.90039a0[13]. 在“凍結核”近似下采用Jacobi坐標(R,θ)來描述體系的幾何構型, 其中R為Kr原子到CS分子質心的距離,θ為R與CS分子軸線之間的夾角,θ=0°對應Kr-S-C構型.

在超分子近似下, 體系相互作用能V(R,θ)可以表示為體系總能量與兩個單體能量之差, 即:

V(R,θ)=EKr-CS-EKr-ECS

(1)

計算中采用Boys和Bernardi的均衡法(Full Counterpoise)對基組重疊誤差(BSSE)進行校正[14], 即:

V(R,θ)=EKr-CS[χKr+χCS]-

EKr[χKr+χCS]-ECS[χKr+χCS]

(2)

其中,χ表示基組. 本文在6.5a0≤R≤25a0, 0°≤θ≤180°區間內共計算了507個幾何構型的離散相互作用勢. 所有的從頭算均在molpro 2006程序包[15]中完成.

用Bukowski[16]等人的解析勢函數將Kr-CS體系的相互作用勢表示為長程相互作用與短程相互作用之和. 本文用分步法進行勢能函數擬合[17], 得到勢能解析函數的50個參數. 通過該方法解析擬合得到體系相互作用勢方均根差和最大絕對誤差分別為0.020 cm-1和0.099 cm-1.

2.2 Kr-CS體系束縛態的計算

在分子坐標系下, 將z軸固定在R上, 用Jocobi坐標表示體系的振轉Hamiltonian為[18, 19]:

(3)

(4)

(5)

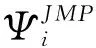
(6)

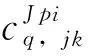
Hqjk,q′j′k′=δqq′δjj′δkk′[Eq+bCSj(j+1)+

∑〈χq|Vλ(R)-V(R,θe)|χq′〉

(7)

3 結果和討論

勢能面可以反映范德瓦爾斯體系分子間相互作用勢的很多信息[20]. 圖1為Kr-CS體系勢能面的等高圖. 由圖可見, 該體系在R=7.76a0處存在一個近T型(θ= 111.4°)的全域極小值, 其值為-178.54 cm-1. 線性構型Kr-S-C能量( -153.79 cm-1在R=8.30a0,θ= 0°) 比Kr-C-S能量低了近25 cm-1(-128.89 cm-1在R=9.60a0,θ= 180°) . Kr原子從S端接近分子時, 相互作用能大于從C端接近.整個勢能面呈現較強的各向異性. 本課題組之前研究的Kr-CS2體系[19]的勢能面為T型構型, 是因為CS2分子是對稱的線性三原子構型, 該構型的極值位置均位于90°, 而Kr原子與質量更大的CS2分子的相互作用明顯強于與CS分子的相互作用, 這就導致Kr-CS2體系勢能極值( -396.194 cm-1) 遠大于Kr-CS體系. 從表1可以看出, Kr-CS體系與He/Ar-CS體系勢能面特征類似, 都是近T型結構, 但是相比He、Ar原子, Kr原子和CS分子間相互作用更強, 其勢阱位置和阱深比He/Ar-CS體系[8, 9]要更遠及更深些, 這主要是因為這三個體系中Kr原子具有最大的極化率. Rg原子和CS分子相互作用特征和與同族CO分子相互作用特征[2]類似.

表1 Rg-CS體系勢能面的極小值位置(R(a0),θ(°) )及相應能量(V(cm-1) )

Table 1 The location (R(a0) ,θ(°) ) and the corresponding energy (V(cm-1) ) of the minimum for the Rg-CS complex

SystemBasis setRθVRefHe-CSpVQZ+332217.25105.0-21.768Ar-CSpV5Z7.49109.3-149.109Kr-CSpV5Z+332217.76111.4-178.54this work

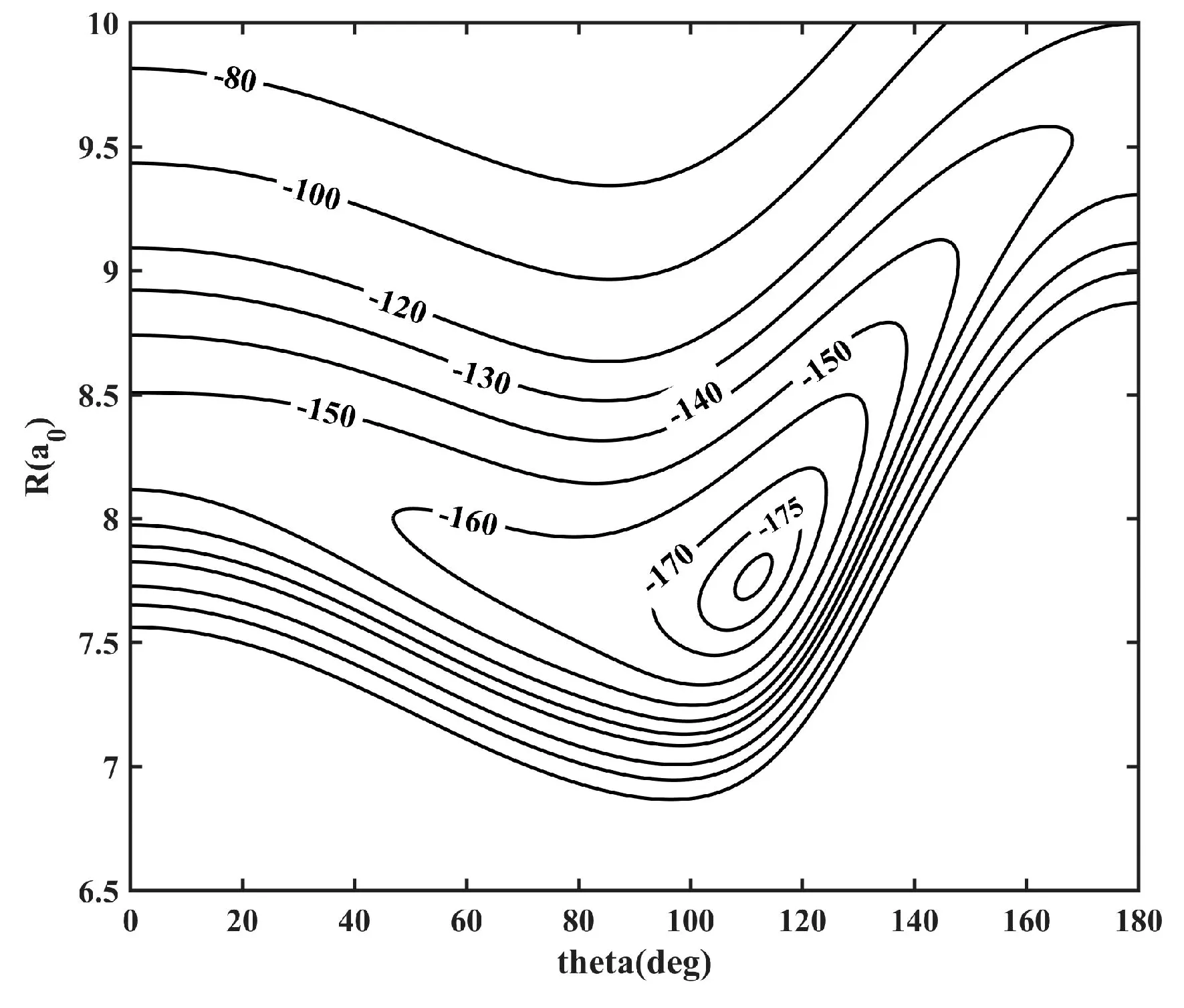
圖1 Kr-CS體系勢能面等高圖(cm-1)Fig. 1 Contours of the potential energy surface of Kr-CS system (cm-1 )

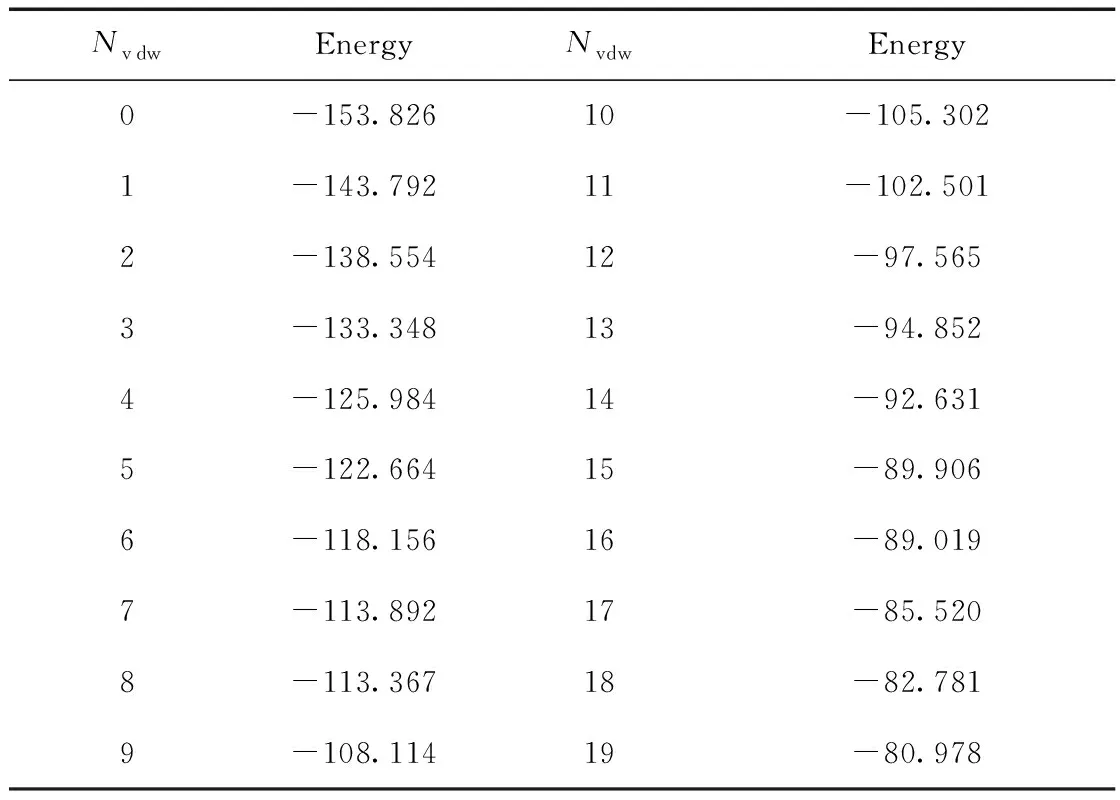
表2 Kr-CS體系前20個低振動激發態(J= 0)的能級(cm-1)

Table 2 The first 20 vibration energy levels (J= 0) of the Kr-CS complex (cm-1)

NvdwEnergyNvdwEnergy0-153.82610-105.3021-143.79211-102.5012-138.55412-97.5653-133.34813-94.8524-125.98414-92.6315-122.66415-89.9066-118.15616-89.0197-113.89217-85.5208-113.36718-82.7819-108.11419-80.978

在求解Kr-CS體系的薛定諤方程時, Legendre多項式的展開項λmax= 15, 基組參數jmax= 30,qmax= 40. 在6.5a0到25a0區間均勻取300個格點求解體系的伸縮振動方程(5) , 得到該體系J≤ 15的振轉能級和波函數. 表2給出了J= 0時,Kr-CS體系前20個低振動激發態的能級, 從表中可以看出體系的基態能級為-153.826 cm-1, 則該體系的零點能為24.714 cm-1. 該零點能與Kr-CO體系[2]零點能( 24.054 cm-1) 很接近，但是比Kr-CS2體系[19]的零點能( 36.360 cm-1) 要小, 主要是因為Kr-CS2體系間有較強的相互作用. 對于Kr-CS的振轉能級還可以用JKaKc來標識, 其中J是體系的總角動量,Ka和Kc分別代表在轉動慣量主軸a和c上的投影[17]. 對于不對稱陀螺,Ka即代表轉動慣量在Z軸上的投影,Kc由p×(-1)J來決定, 其中p為波函數的宇稱. 表3給出了標定的部分轉動能級, 由表中可以看出, 該體系的能級有簡并, 比如221和220能級, 其能量均為-150.054 cm-1. 依照所求的純轉動能級, 根據選擇定則, 就可以得到體系的微波譜躍遷頻率. 表4即給出了Kr-CS體系微波譜躍遷頻率(a型躍遷R支) , 其選擇定則為ΔJ=1,ΔKa=0,ΔKc=±1.

為了更直觀地反應束縛態的分布情況，我們還畫出了Kr-CS體系J= 0的前四個振動能級的波函數等高圖, 如圖2所示. 圖(a)對應基態能級, 從圖中可以看出該態主要落在全局勢阱中. 圖(b)為第一激發態能級, 其能量為-143.792 cm-1, 從波函數節點可以看出該激發態是彎曲振動, 由此可得彎曲振動基頻為10.034 cm-1. 圖(c)為第二激發態能級, 其值為-138.555 cm-1, 該能級是彎曲振動和伸展振動的混合, 但是從圖中可以看出, 主要還是對應兩個彎曲振動量子數.第三激發態能級為-133.348 cm-1, 該激發態主要是兩個彎曲振動激發混合著一個伸展振動激發. 而較高能級的波函數均為彎曲振動和伸展振動的混合. 該波函數特征與Kr-CO的波函數特征[2]很相似, 這說明Kr原子與CS分子的相互作用可類比于Kr-CO體系.

表3 Kr-CS 體系純轉能級值( cm-1)

Table 3 The calculation pure rotational energy levels of the Kr-CS complex (cm-1)

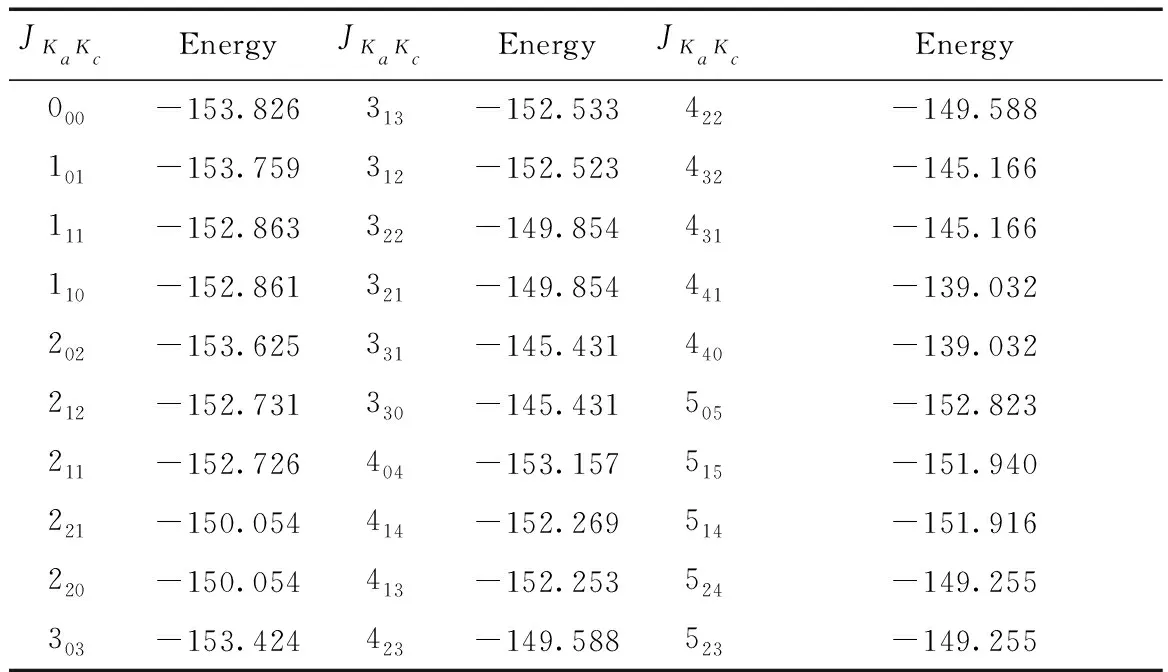
JKaKcEnergyJKaKcEnergyJKaKcEnergy000-153.826313-152.533422-149.588101-153.759312-152.523432-145.166111-152.863322-149.854431-145.166110-152.861321-149.854441-139.032202-153.625331-145.431440-139.032212-152.731330-145.431505-152.823211-152.726404-153.157515-151.940221-150.054414-152.269514-151.916220-150.054413-152.253524-149.255303-153.424423-149.588523-149.255

表4 Kr-CS的微波譜躍遷頻率 (cm-1)

Table 4 The calculated microwave transition frequencies (in cm-1)of Kr-CS complex

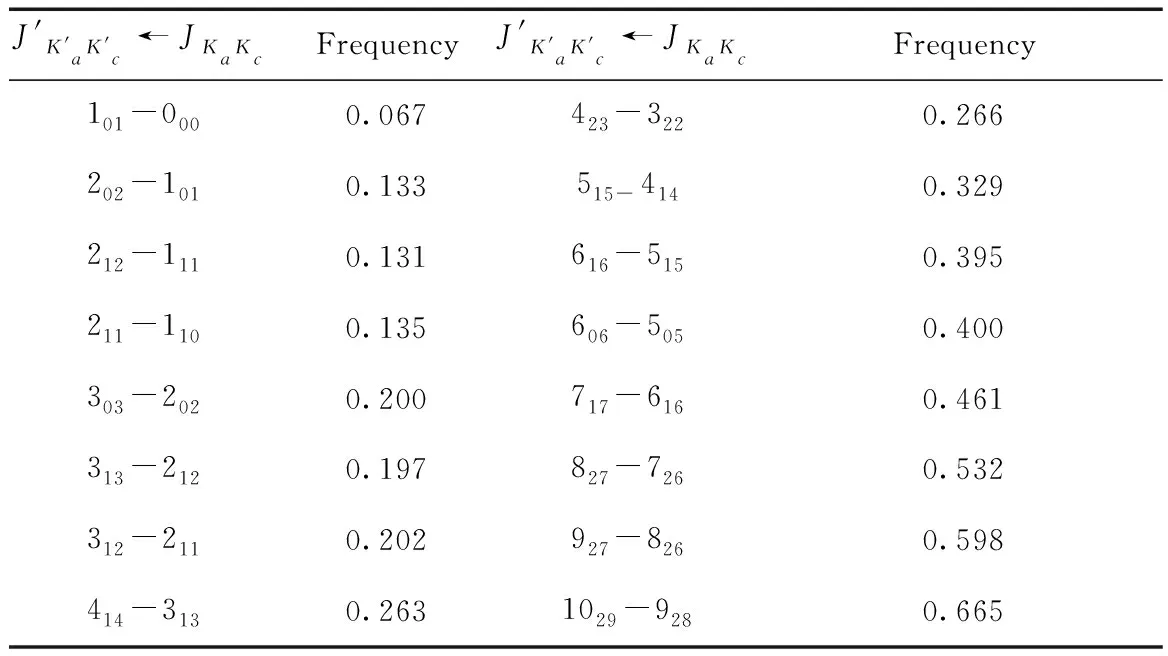
J'K'aK'c←JKaKcFrequencyJ'K'aK'c←JKaKcFrequency101-0000.067423-3220.266202-1010.133515-4140.329212-1110.131616-5150.395211-1100.135606-5050.400303-2020.200717-6160.461313-2120.197827-7260.532312-2110.202927-8260.598414-3130.2631029-9280.665

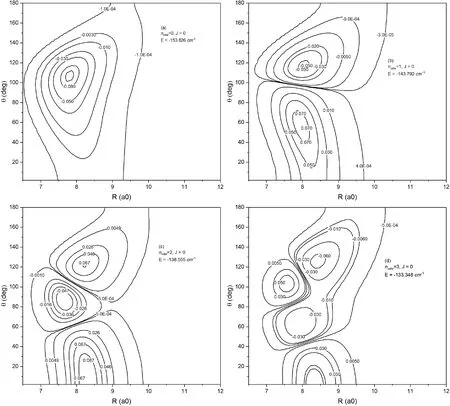
圖 2 Kr-CS體系前四個振動能級 (J = 0) 的波函數等高圖Fig. 2 Contours of the wave functions for the first four vibration levels (J = 0) of Kr-CS complex

4 結 論

本文在CCSD(T)理論基礎上, 對范德瓦爾斯體系Kr-CS的507個構型下的離散相互作用勢進行了計算, 通過解析擬合得到的勢能面為近T型結構. 線性構型Kr-S-C能量比Kr-C-S能量低了近25 cm-1. 存在全局極小值在R= 7.76a0,θ= 111.4°處, 其勢能值為-178.54 cm-1.R、θ及V值均如預期效果較He/Ar-CS體系增大. 在該勢能面基礎上數值求解了體系的薛定諤方程, 計算并得到體系的J≤ 15的束縛態能級, 并預測了體系a型躍遷R支微波譜躍遷頻率. 從波函數特征上可以看到, CO分子和CS分子與Kr原子相互作用具有相似性. 這些結果將對實驗工作具有理論指導作用.