關于單元體系Cu的玻璃轉變過程中動力學不均勻性的研究

幸曉鳳， 孫永麗, 王智聰

(太原理工大學 物理與光電工程學院， 太原 030024)

1 引 言

非晶合金由于具有優異的力學、物理和化學性能，成為備受歡迎的新型合金材料[1-3]. 而不均勻性是非晶態體系[4-7]的固有性質，這些不均勻性與材料的諸多性能密切相關. 因此研究動力學不均勻性有助于理解物質的各種性能. 在非晶態研究中，可以建立理想的模型體系，能直觀地反映各種性能，并在Cu-Zr[8-10]、Cu-Zr-Al[11,12]等合金領域取得不菲成就.

利用分子動力學模擬技術研究了單元體系Cu玻璃轉變過程中動力學不均勻性，因單元體系Cu結構簡單，無需考慮多種元素之間的作用力. 并用非高斯參數α2(t)揭示動力學不均勻性的存在，且溫度越接近玻璃轉變溫度Tg，其動力學不均勻性越明顯. 目前相關研究[13-15]只定性的研究了非高斯參數α2(t)隨時間的變化趨勢，但定量關系未過多涉及. 故本文定量的研究了β弛豫中非高斯參數α2(t)隨時間，非高斯參數峰值αmax以及β弛豫時間τβ隨溫度的變化關系.

2 模擬條件及方法

將10976個Cu原子隨機排列成FCC晶格，并放置于14×14×14的立方體盒子中. 基于系統的總能量為EAM勢[16]下，采用等溫等壓(NPT)系綜，在周期性邊界條件下，壓強為0 Gpa，初始溫度為2000 K，時間步長為0.001 ps，運行一段時間確保體系達到平衡狀態，然后以1.0×1014K/s的冷卻速率降溫到300 K. 整個降溫過程采用梯度方式，每降溫100 K，運行一段時間確保體系達到平衡，并輸出相關參數.

3 模擬計算結果與分析

3.1 熔點Tm及玻璃轉變溫度Tg分析

加熱的過程中，體系的內能和體積與溫度滿足線性關系，但當溫度達到熔點Tm時，能量和體積曲線發生較大的跳躍. 圖1紅點表示單元體系Cu加熱過程中平均原子體積隨溫度的變化，發現在1800 K～1900 K之間出現突變點，即一級相變，確定了單元體系Cu的熔點Tm為1850 K. 圖中玻璃轉變溫度Tg與熔點Tm之間的區域，稱之為過冷液相區. 玻璃轉變溫度Tg是判斷非晶形成能力的重要參數之一[17]，在模擬過程中通常使用體積判別方法[18]來確定其大小. 圖1中黑點表示單元體系Cu冷卻過程中平均原子體積隨溫度的變化，可見其變化曲線是連續的，表明體系已經形成非晶結構，并得到單元體系Cu的玻璃轉變溫度Tg為900 K.

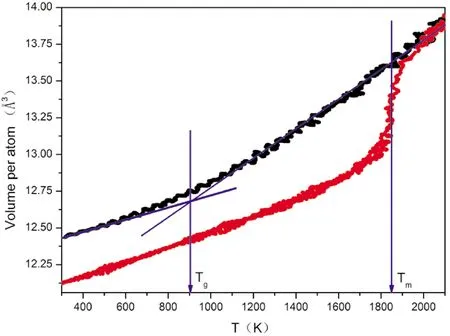
圖1 體積隨溫度的變化(紅：加熱過程；黑：冷卻過程)Fig. 1 The variation of volume with temperature (red: heating process; black: cooling process)

3.2 徑向分布函數RDF分析

徑向分布函數RDF是用來描述液態和非晶態的一種重要結構參數，它表示以任意一個原子為中心，半徑為r到r+dr兩個球殼之間發現另一個原子的概率[19]. 圖2表示單元體系Cu的徑向分布函數RDF隨溫度的變化，為使結果清晰可見，對不同溫度的曲線進行縱向平移. 淬火過程中，第一峰的高度隨溫度的降低而增加，寬度逐漸減小，表明原子結構的有序性隨著溫度的降低越來越強，原子之間的聯系越來越緊密. 同時發現900 K時，第二峰發生劈裂，而且第一次峰的高度要比第二次峰高. 低溫時第二峰的劈裂，表明單元體系Cu的過冷液態和玻璃態的形成，進一步確定了單元體系Cu的玻璃轉變溫度Tg為900 K.

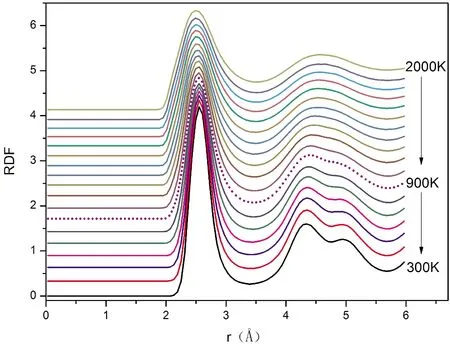
圖2 徑向分布函數RDF隨溫度的變化Fig. 2 Radial distribution function RDF curves at different temperatures

3.3 均方位移MSD分析

均方位移MSD描述了體系中原子在t時間內的平均位移的平方. 通過均方位移MSD隨時間的變化，來研究原子的遷移率. 圖3為不同溫度下單元體系Cu的均方位移MSD隨時間的變化. 高溫條件下，均方位移MSD表現出對時間的線性依賴，即為液體行為. 隨溫度的降低，均方位移MSD出現平臺區，且溫度越低，平臺區越明顯，單個粒子的遷移所受限制越大.

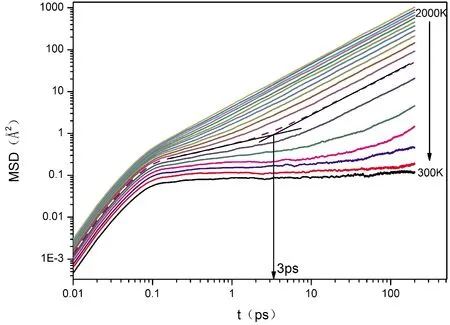
圖3 均方位移MSD隨溫度的變化Fig. 3 Mean-squared displacement MSD curves at different temperatures

在短時間內(小于0.1 ps)，均方位移MSD隨時間增加較快，此時原子做自由振動. 隨溫度的降低，均方位移MSD的數值略有下降. 但在長時間擴散區域(超過3 ps)，溫度高于900 K時，均方位移MSD增加比較快，此時原子做長程擴散運動. 而在中間區域(0.1 ps ～ 3 ps)，900 K的均方位移MSD斜率相比高溫變小，此時有些原子做簡諧振動，有些原子做擴散運動. 結果表明溫度越低，均方位移MSD斜率越小，粒子運動越慢，動力學不均勻性越強.

3.4 非高斯參數α2(t)

通過計算非高斯參數α2(t)測量原子分布與高斯漲落的偏差，進一步研究動力學不均勻性的變化. 一般，α2(t)=0說明原子做簡諧振動或隨機運動，其位移符合高斯分布；α2(t)>0，表明原子偏離了隨機運動的規律. 非高斯參數峰值αmax表示動力學不均勻程度，能反映粒子周圍局域環境的不同. 不同溫度下非高斯參數α2(t)隨時間的變化如圖4，可見時間小于0.1 ps，α2(t)=0表明原子運動在振動過程中滿足高斯分布. 當時間為0.1 ps ～τβ(非高斯參數α2(t)最大時，特征時間t=τβ，即τβ表示β弛豫時間)時，系統進入β弛豫，粒子運動服從非高斯分布. 從動力學角度看，系統進入原子位移分布范圍最廣的不均勻狀態.

如圖4，在β弛豫中不同溫度下非高斯參數α2(t)隨時間的的變化趨勢是一致的，原子運動的非高斯行為具有相同的規律. 因此，通過對不同溫度下的曲線擬合，發現非高斯參數α2(t)與時間t的關系滿足冪律函數[20](圖4中紅線):α2(t)=α0×(t-t0)γ，其中指前因子α0=0.29，β弛豫開始時刻t0=0.1，指數γ=0.49.

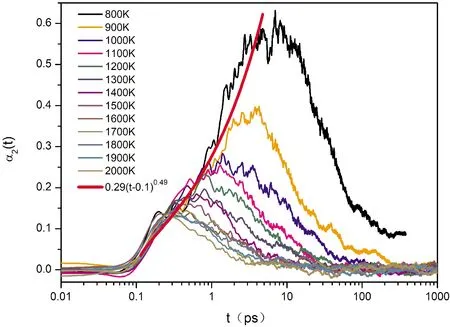
圖4 不同溫度下Cu的非高斯參數α2(t)及擬合曲線Fig. 4 Non-Gaussian parameter α2(t) and fitting curve of Cu at different temperatures

當時間大于β弛豫時間τβ時，系統進入α弛豫階段，非高斯參數α2(t)的值從最大值逐漸減小，最終趨于0. 900 K～2000 K的非高斯參數α2(t)最終達到0，表明原子擴散動態特性滿足高斯分布. 溫度為800 K時，非高斯參數α2(t)未達到0，說明體系的結構弛豫時間不充分. 另外，在α弛豫過程中，各溫度曲線的斜率存在顯著的差異，表明系統在不同溫度下的結構弛豫規律是不同的.

在圖5中藍點表示β弛豫時間τβ與溫度的關系，發現隨著溫度的降低，β弛豫時間τβ變長，可見體系溫度越低，達到動力學最不均勻狀態所需要的時間越長，而溫度比較高時(T>1200 K)，β弛豫時間τβ增加緩慢. 同時β弛豫時間τβ隨溫度T的變化遵循Arrhenius函數[21](圖5中藍線)：τβ=τ0exp(-E/KBT)，其中指前因子τ0=0.04 ps, 激活能E=0.36 eV，玻爾茲曼常數KB=1.38×10-23J/K. 為進一步闡明動力學不均勻性與溫度的關系，圖5黑點表示非高斯參數峰值αmax隨溫度的變化，發現在800 K～1000 K范圍內顯著增大，而當溫度高于1500 K時非高斯參數峰值αmax增加緩慢，通過對數據點的擬合，非高斯參數峰值αmax與溫度T滿足Arrhenius函數(圖5中黑線)：αmax=α0exp(-E/KBT)，其中指前因子α0=0.02 ，激活能E=0.18 eV. 結果表明單元體系Cu玻璃轉變過程中，溫度越接近玻璃轉變溫度Tg，其動力學不均勻性越強.

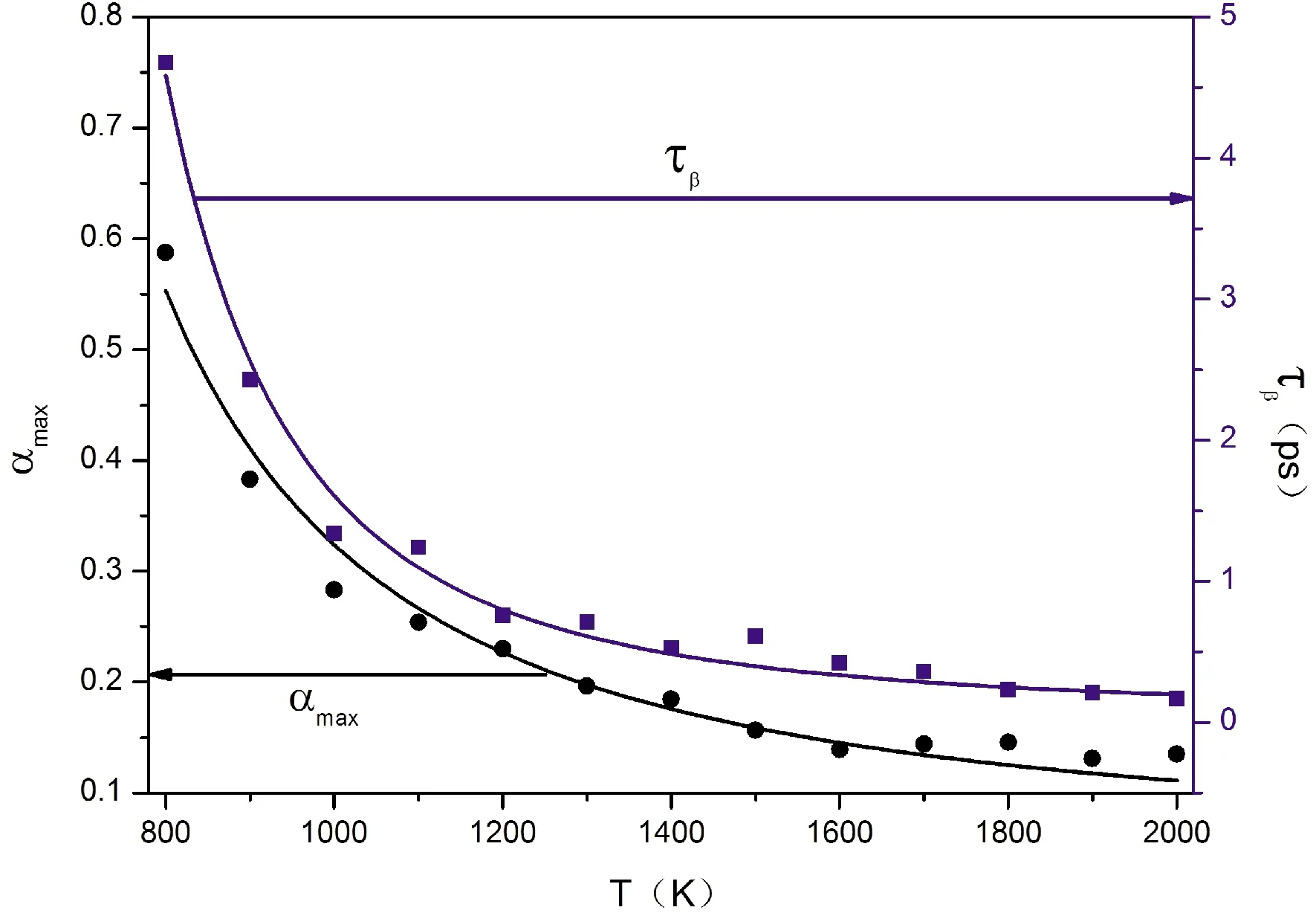
圖5 非高斯參數峰值αmax和β弛豫時間τβ隨溫度的變化Fig. 5 The peak values of the non-Gaussian parameter αmax and the β relaxation time τβ at different temperatures

4 總 結

本文基于分子動力學模擬技術，利用非高斯參數α2(t) 研究單元體系Cu玻璃轉變過程中動力學不均勻性的變化，得出以下結論：

(1)通過對單元體系Cu玻璃轉變過程中平均原子體積隨溫度的變化以及徑向分布函數RDF，最終確定單元體系Cu的玻璃轉變溫度為900 K. 并研究了不同溫度下原子均方位移MSD隨時間的變化規律，發現溫度會影響體系的動力學性質，體系溫度越低，均方位移MSD斜率較小，表現出動力學不均勻性越強.

(2)單元體系Cu玻璃轉變過程中，β弛豫階段非高斯參數α2(t)隨時間的變化符合冪律函數，而且隨著體系溫度的降低，非高斯參數峰值αmax逐漸增加，并向長時間區域移動，表明體系中存在動力學不均勻性，而且這種不均勻性程度隨著溫度的降低而逐漸增強. 同時發現非高斯參數峰值αmax及β弛豫時間τβ與溫度T的關系均符合Arrhenius函數.