非簡諧振動對SiC類石墨烯熱輸運性質的影響

周虹君, 鄭瑞倫, 王明亮

(1. 重慶新型儲能器件及應用工程研究中心， 重慶 402160; 2. 重慶文理學院電子電氣工程學院， 重慶 402160; 3. 重慶市第八中學校， 重慶 402160)

1 引 言

石墨烯的獨特性質引起人們對其它類似的二維六角結構的物質—類石墨烯物質極大的興趣，并且已有不少文獻對它們的制備和性能進行研究. 文獻[1-3]用密度泛函方法研究了SiC等AN-B8-N二元二維類石墨烯化合物的穩定性，證明了這些化合物可以存在. 文獻[4]利用哈里森提出的鍵聯軌道法，研究了AN-B8-N類石墨烯的彈性和介電性質，文獻[5]研究了SiC的π鍵對類石墨烯化合物的有效電荷、內聚能和力常數的貢獻，文獻[6]還研究了SiC類石墨烯的彈性，但這些研究并未探討它的熱容量和熱導率等這些具有重要理論和應用價值的熱輸運性質的變化規律，而且在研究中，認為原子靜止，未考慮到原子的振動，特別是原子的非簡諧振動，因而反映不出這些熱力學量隨溫度的變化規律. 為克服現有文獻的局限性，最近，文獻[7]考慮到原子的非簡諧振動，研究了SiC類石墨烯的熱膨脹系數和介電性能，但未研究熱容量和熱導率等熱輸運性質，而且計算它的原子相互作用能和原子振動的簡諧系數和非簡諧系數時，未考慮原子間的短程相互作用. 鑒于熱輸運性質在理論和應用上的重要性，本文將在考慮到原子作非簡諧振動和原子間存在短程相互作用情況下，對這一問題進行研究，并探討原子非簡諧振動對它們的影響.

2 物理模型和原子振動的簡諧系數和非簡諧系數

類石墨烯化合物是由A原子和B原子構成的二維六角格子平面系統(如圖1)，設A原子和B原各自總原子數為N，最近鄰原子間距離為d(稱點陣常數)，取任一原子為坐標系原點，平面為OXY平面，Z軸垂直向上，坐標系選取見圖1.

圖1 SiC類石墨烯系統俯面Fig. 1 SiC graphene-like system pitch

不考慮短程相互作用時，原子相互作用能φ為σ鍵和π鍵貢獻的和[5]：

φ0(d)=Ebσ+Ebπ

(1)

考慮短程相互作用時，SiC的原子相互作用能為：

(2)

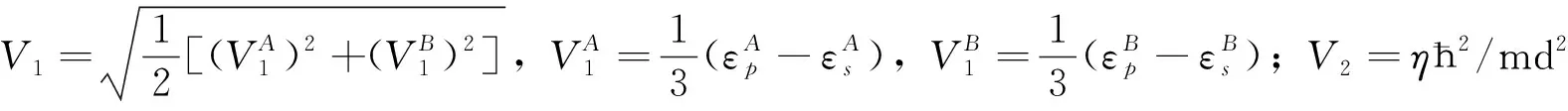
(3)

簡諧系數反映原子相互作用的強弱，而非簡諧系數是原子振動非簡諧效應的定量表示. 由(1)式求得不考慮短程作用時的簡諧系數ε0=(?2φ/?d2)0為：

(4)

進而求得第一非簡諧系數εl=(1/6)(?ε0/?d)0和第二非簡諧系數ε2=(1/4)(?ε1/?d)0為：

(5)

(6)

考慮到原子間的短程作用后，簡諧系數為：

ε0=ε0σ+ε0π

(7)

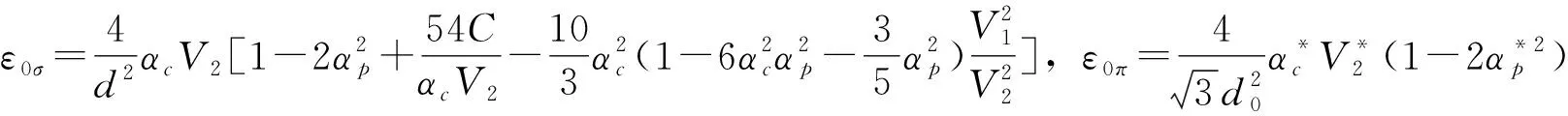
第一非簡諧系數ε1和第二非簡諧系數ε2分別為：

(8)

(9)

3 德拜溫度、熱容量、熱導率隨溫度的變化

德拜溫度是材料的特征溫度，是原子都以最大頻率振動時系統的溫度，許多熱學性質(如熱容量、熱導率、聲子運動自由程等)都與它有關. 簡諧近似下的德拜溫度θD0(即T=0 K時的德拜溫度)與簡諧系數ε0關系為[9]：

(10)

式中的?和kB分別是普朗克常數和玻爾茲曼常數，而M為SiC的折合原子質量，對SiC這類二元化合物，與C和Si元素原子質量的關系為：

(11)

考慮到原子振動的非簡諧效應后，利用振動頻率與溫度的如下關系[10]：

(12)

得到德拜溫度與簡諧系數和非簡諧系數的關系為：

(13)

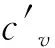
(14)

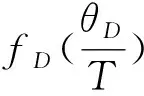
(15)

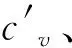
(16)

式中的聲子平均速度v可由下式求得：

(17)

這里的vl、vT分別為縱聲子和橫聲子相應的格波的波速.

在溫度不太高和不太低時的聲子平均自由程l與溫度T的關系為：

(18)

這里η是與物質有關的2-3之間的參數，l0是待定參量，它可由某一溫度下已知的熱導率的值來確定. 由(16)式可得到通常溫度下晶格熱導率K隨溫度的變化.

4 非簡諧振動對SiC類石墨烯德拜溫度、熱容量、熱導率的影響

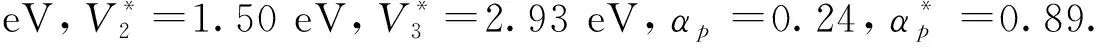
表1 SiC類石墨烯的德拜溫度θD隨溫度T的變化

其變化曲線見圖2，其中線1為簡諧近似時的德拜溫度；線2為考慮到第一非簡諧項后的德拜溫度；線3為考慮到第一、二非簡諧項的德拜溫度. 由圖2看出：簡諧近似下SiC類石墨烯的德拜溫度為常數θD0=117.0 K；考慮到非簡諧振動項后，SiC的德拜溫度隨著溫度的升高而在117 K-126 K之間線性增大； 非簡諧情況的德拜溫度與簡諧近似下的值的差也隨著溫度升高而增大，即溫度愈高，非簡諧效應對德拜溫度的影響愈顯著.

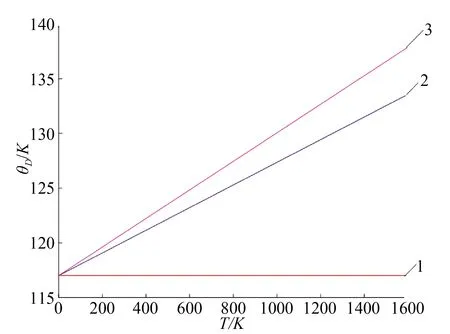
圖2 SiC類石墨烯的德拜溫度隨溫度的變化Fig 2 Variation of Debye Temperature of SiC graphene with Temperature

將求得的SiC的μ、θD(T)和氣體普適常數R=8.31 J·mol-1·K-1代入(14)、(15)式，可得SiC類石墨烯的晶格定容比熱隨溫度的變化數據見表2. 變化曲線如圖3，其中線1為簡諧近似時的定容比隨溫度變化曲線；線2為考慮到第一非簡諧項后的定容比隨溫度變化曲線；線3為考慮到第一、二非簡諧項的定容比隨溫度變化曲線. 表中的(1)、(2)、(3)分別是簡諧近似、只考慮到第一非簡諧項、同時考慮到第一、第二非簡諧項的定容比熱的結果.

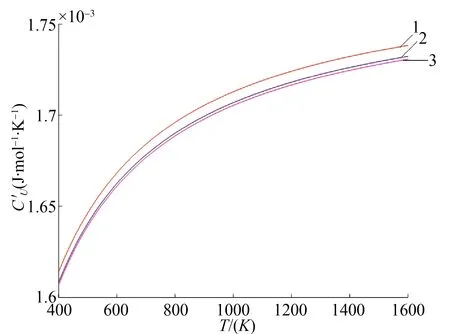
圖3 SiC類石墨烯的晶格定容比熱隨溫度的變化Fig. 3 Variation of lattice constant and volume specific heat of SiC graphene with temperature

由圖3可以看出：(1)SiC類石墨烯的晶格定容比熱隨著溫度的升高而增大, 其中溫度較低時變化較快，而溫度較高時變化較慢，高溫時趨于2R；它與SiC塊狀晶體的變化情況(見文獻[12])類似，但有區別(塊狀晶體高溫時趨于3R)；(2)相同溫度下，非簡諧情況的熱容量比簡諧近似的值稍小，即非簡諧效應使SiC類石墨烯的定容比熱減小，而且溫度愈高，其影響愈顯著.

由于SiC類石墨烯與石墨烯具有相似結構，因此SiC類石墨烯中縱聲子和橫聲子相應格波的波速應與石墨烯中的格波波速近似相同，它的聲子平均自由程l與溫度T的關系相似. 按文獻[13]，取vl=21.04×103m·s-1，vT=14.09×103m·s-1，由(17)式得到聲子平均速度v=16.9398 km·s-1. 文獻[14]給出石墨烯的l0=2.593×10-4m. 將l0、η=2、θD(T)等代入(18)式，求得l(T)，與(14)式一起代入(16)式，可得到SiC類石墨烯的熱導率隨溫度的變化見表3，變化曲線如圖4. 其中線1為簡諧近似時的熱導率隨溫度變化曲線；線2為考慮到第一非簡諧項后的熱導率隨溫度變化曲線；線3 為考慮到第一、二非簡諧項的熱導率隨溫度變化曲線. 其中表(1)、(2)、(3)分別是簡諧近似、只考慮到第一非簡諧項、同時考慮到第一、第二非簡諧項的熱導率結果.

表2 SiC定容比熱隨溫度的變化

表3 SiC的熱導率隨溫度的變化

圖4 SiC類石墨烯的熱導率隨溫度的變化Fig. 4 Variation of thermal conductivity of SiC graphene with temperature

由圖4可看出：(1)SiC類石墨烯的熱導率隨著溫度的升高而非線性減小，其中溫度較低時變化較快，而溫度較高時變化較慢，并隨著溫度的升高而趨于常量K=2.5 W·cm-1·K-1；(2)相同溫度下，非簡諧情況的熱導率比簡諧近似的值稍大，即非簡諧效應使SiC類石墨烯的熱導率增大，而且溫度愈高，其影響愈顯著. 例如：T=400 K時，兩者的差為ΔK=5.7×10-3W·cm-1·K-1，而T=700 K時，兩者的差為ΔK=5.8×10-3W·cm-1·K-1；(3)二維系統的SiC類石墨烯其熱導率隨溫度的變化與文獻[15][16]給出的三維塊狀SiC晶體的熱導率隨溫度升高而不斷減小的變化規律總體趨勢相同，只是數值有差異. SiC類石墨烯數值大于三維塊狀SiC晶體的熱導率(絕對零度時為0.396 W·cm-1·K-1).

5 結 論

本文對SiC類石墨烯德拜溫度、熱容量、熱導率等性質隨溫度的變化規律的研究表明：

(1)SiC類石墨烯的德拜溫度隨溫度升高而在117 K-126 K之間線性增大，定容比熱隨溫度升高而非線性增大，而熱導率隨溫度升高而非線性減小，其中溫度較低時變化較快，而溫度較高時變化較慢，并隨著溫度的升高而趨于常量，其具體變化分別由(13)、(14)和(16)表示；

(2)考慮到非簡諧振動后，SiC類石墨烯的德拜溫度、定容比熱和熱導率的值分別大于、小于和大于簡諧近似下的相應值，且溫度愈高，其差值愈大，即溫度愈高，非簡諧效應對SiC類石墨烯熱力學性質的影響愈顯著；

(3)作為二維系統的SiC類石墨烯的定容比熱和熱導率隨溫度的變化規律，與作為三維塊狀SiC晶體其隨溫度的變化規律，總體趨勢相同.