德拜模型和自洽場離子球模型屏蔽效應的比較

李向富， 李高清， 賈利平， 蔣 剛

(1. 隴東學院電氣工程學院， 慶陽 745000； 2. 四川大學原子與分子物理研究所， 成都 610065；3. 四川大學高能量密度物理及技術教育部重點實驗室， 成都 610065)

1 引 言

在等離子體中，離子處在自由電子和帶電離子所產生的勢場中，使得離子的諸多特性發生了不同程度的改變，如譜線移動、譜線展寬、譜線合并、能級交叉和電離勢衰落等. 通過對離子這些獨特性質的測量和計算可以確定等離子體的密度、溫度和電離度等狀態參量，為等離子體物理、溫稠密物質、沖擊實驗、天體物理、高能量密度物理以及核聚變能源等方面提供科學指導[1-11].

2 理論方法

對于包含N個束縛電子的離子，其狄拉克-庫侖哈密頓(Dirac-Coulomb Hamiltonian)可以表示為如下的形式：

(1)

上式中第一項表示單個束縛電子的能量之和，第二項表示束縛電子間的相互作用能. 單電子的HamiltonianHi定義為：

(2)

上式中的第一項和第二項是束縛電子的相對論動能項，最后一項VP(ri)是束縛電子感受到的等離子體屏蔽勢. 下面我們分別來介紹德拜模型和自洽場離子球模型所表述的等離子體屏蔽勢.

在德拜模型中，核電荷數為Z的離子處在原點處，其周圍的靜電勢表達式為：

(3)

上式中D是德拜屏蔽長度，其表達式為：

(4)

(4)式中ne和Te分別表示等離子體中的電子密度和電子溫度.

在自洽場離子球模型(SCFISM)中，假定核電荷數為Z的離子處在一個球形空腔中，該空腔中包含Z個電子，使得整個球形空腔呈電中性狀態，此球形空腔稱為離子球或者韋格納—塞茨(Winger-Seitz)球. 離子球半徑R0由下式確定：

(5)

上式中nf是平均自由電子密度，N是球內束縛電子個數. 將離子球外面的等離子體視為電中性背景，下面介紹如何求解自洽場離子球模型的屏蔽勢.

核電荷數為Z的離子、密度分別為nf(r)和nb(r)的自由電子和束縛電子所產生的總電勢滿足如下的泊松方程[16]：

▽2Vtot=-4π[Zδ(r)-nf(r)-nb(r)]

(6)

束縛電子的密度nb(r)可以用徑向波函數的大小分量P(r)和Q(r)求得，對于一個給定的束縛態，nb(r)可以用下式表示：

(7)

上式中的qi表示次殼層i上束縛電子的占據數，M表示次殼層的個數. 假定離子球中的自由電子遵循費米-狄拉克(Fermi-Dirac)分布，即自由電子密度的定義如下：

(8)

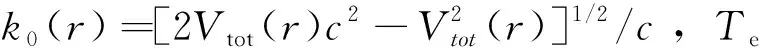
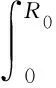
(9)

總電勢的邊界條件為：

Vtot(r≥R0)=0

(10)

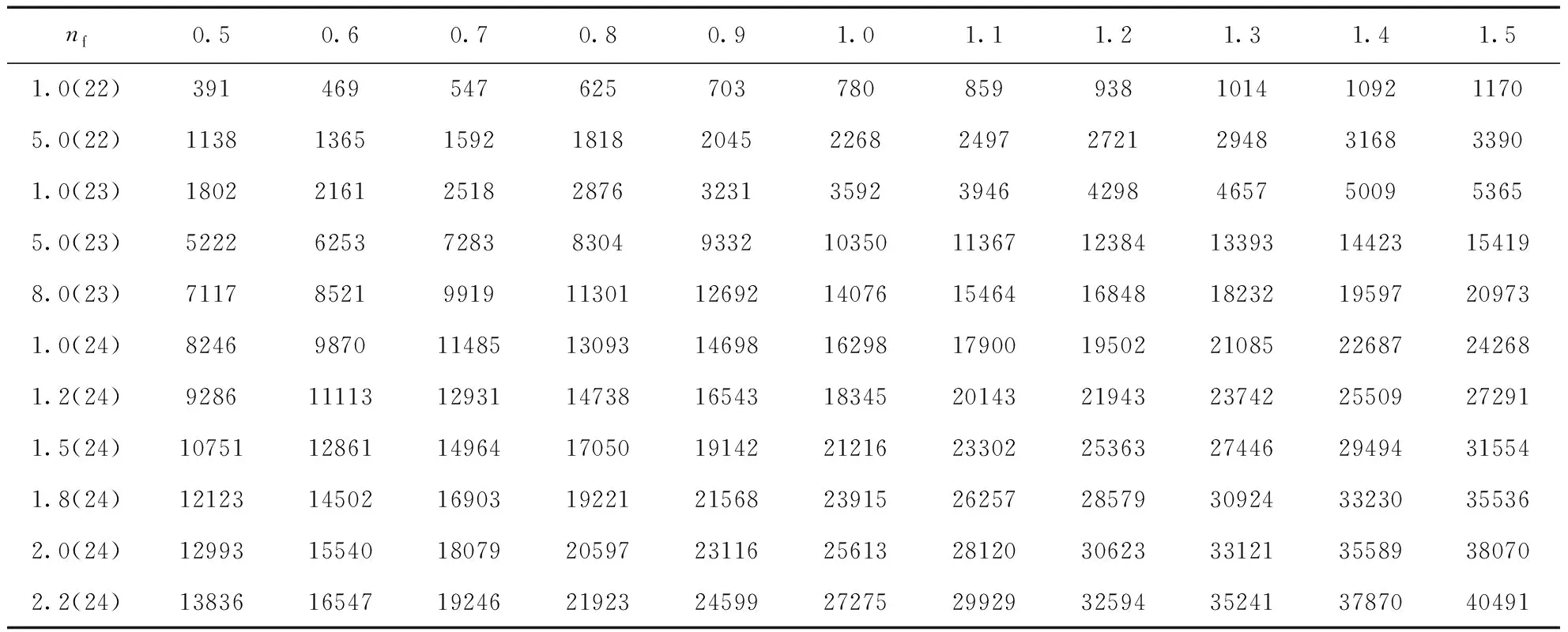
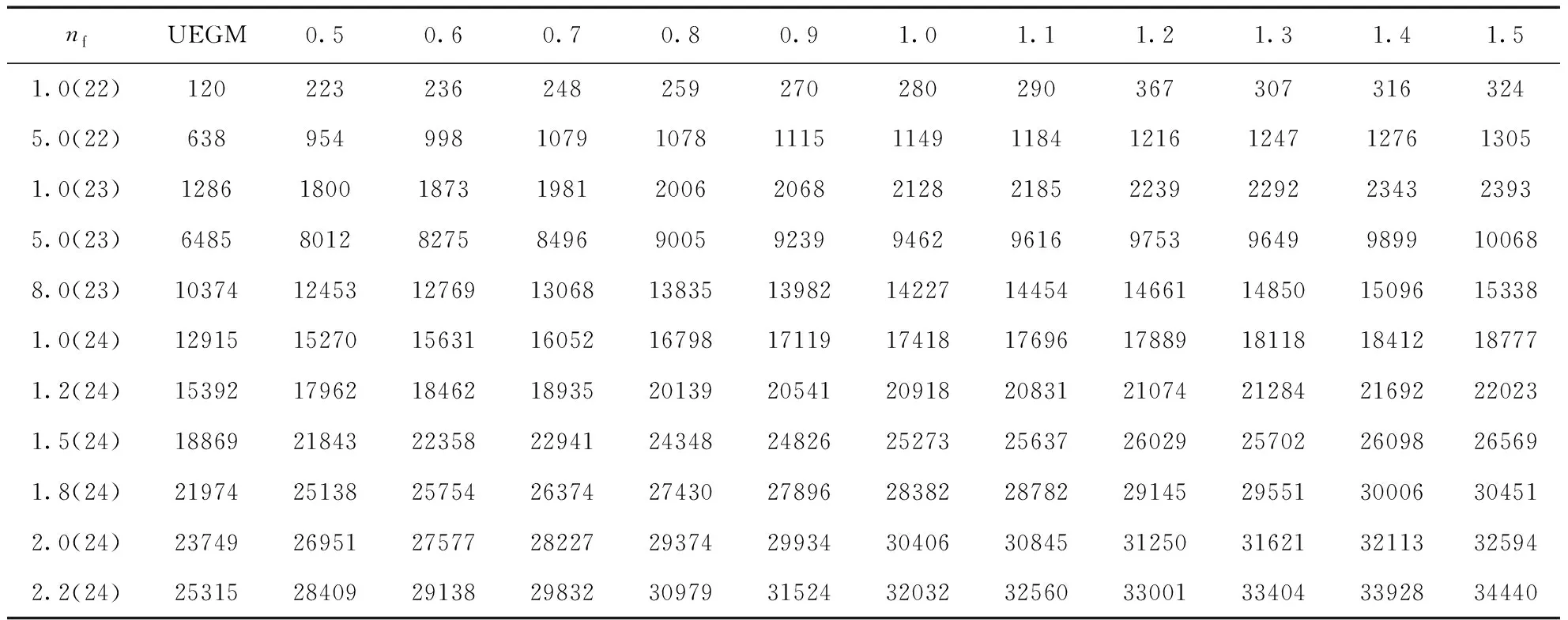
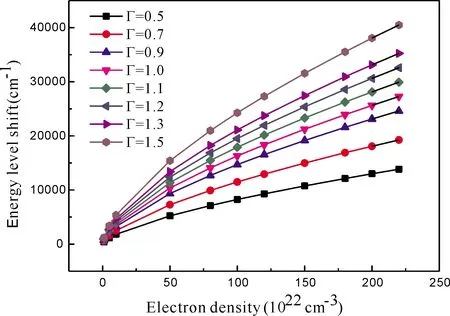
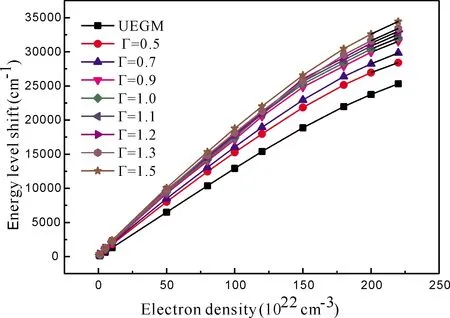
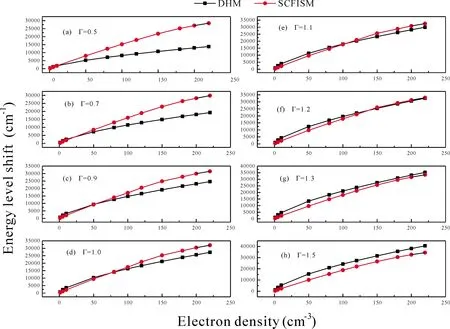
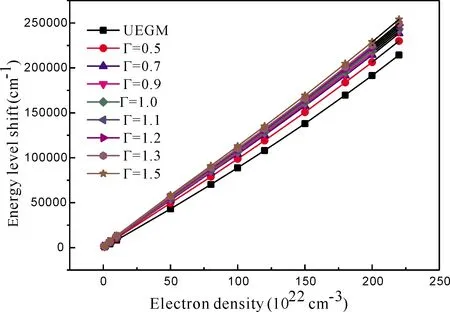
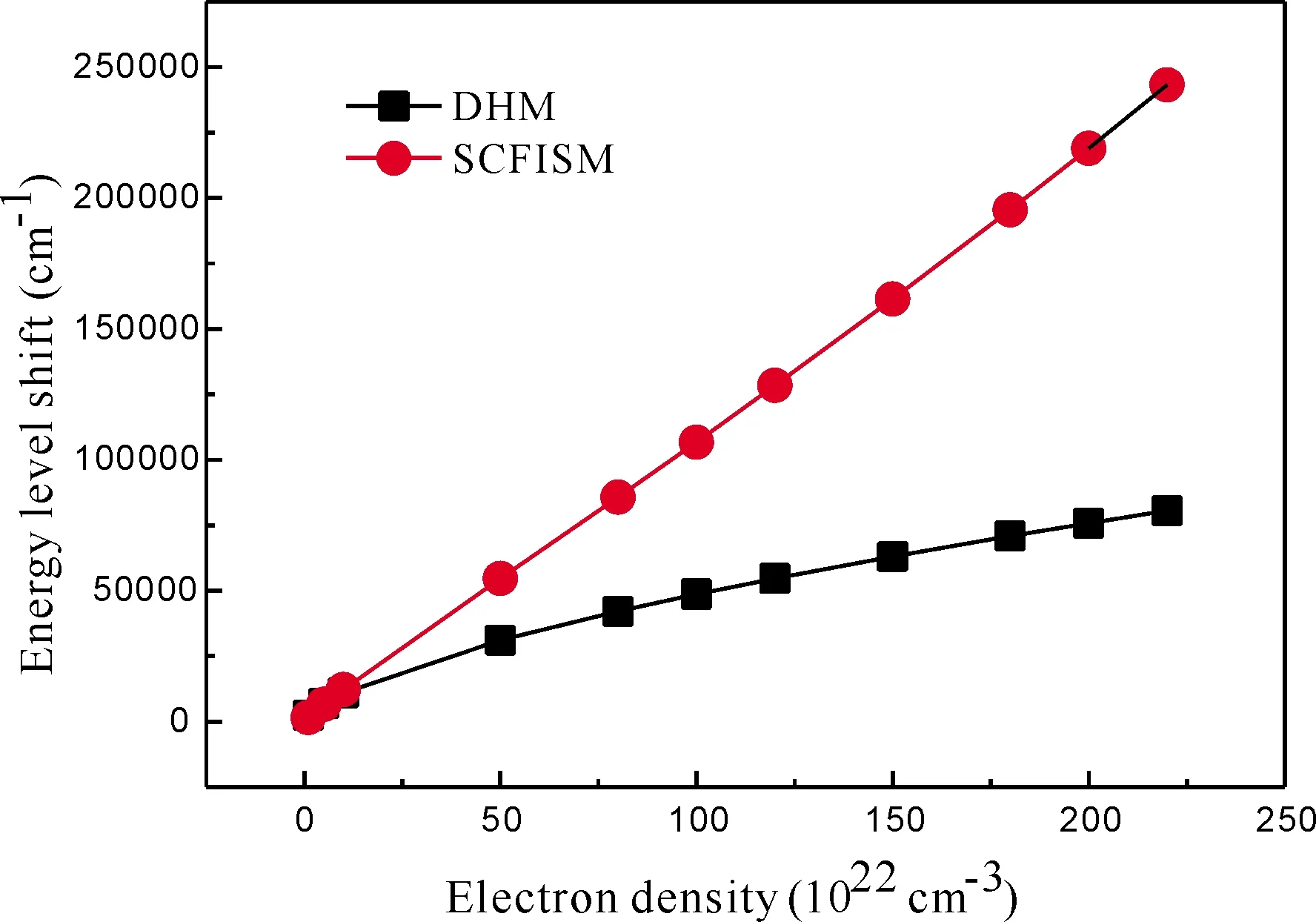
當r

Vtot(r)=Z/r+Vf(r)+Vb(r)

(11)

(11)式包括核、自由電子和束縛電子三者對總電勢的貢獻. 自由電子的電勢由下式計算：

(12)

同理，束縛電子的電勢與自由電子的電勢相似，其表達式如下：

(13)

等離子體屏蔽勢的定義如下：

Vp(r)=Z/r+Vf(r)

(14)

(14)式即是自洽場離子球模型中束縛電子所感受到的有效核勢.

如果電子的溫度較高，以致于自由電子的動能完全克服勢能時，方程(8)式表明此時自由電子的密度分布變得與空間位置無關，此時，有效核勢簡化為如下的均勻電子氣離子球型( UEGM)：

(15)

因為離子球外面的電勢為零，故束縛電子可以運動至離子球外面. 因此，本文中允許束縛電子隧穿至離子球外面，同時維持了整個離子球呈電中性狀態，詳細討論見我們最近的論文[17]. 我們改進后的自洽場離子球模型的徑向波函數邊界條件和德拜模型的一致，即束縛電子徑向波函數的大小分量P(r)和Q(r)滿足以下邊界條件和歸一化條件：

X(0)=0,X(∞)=0 (X=P或者Q)

(16)

(17)

本文采用多組態Dirac-Fock (MCDF)方法[18]描述相對論效應和束縛電子間的關聯效應. 以1s2、1s2p和1s3p為參考組態，分別將這些參考組態上的兩個束縛電子進行雙激發，按主量子數n逐層擴展，并計算原子結構數據，直至所計算的原子結構數據收斂為止. 對于類氦鋁離子，擴展至主量子數n=6即可收斂. 所有的計算工作均在我們改進后的全相對論原子結構計算程序GRASP2K[19, 20]上完成.

3 結果與討論

3.1 不同耦合強度所對應的電子密度和溫度

表1和圖1分別所示的是耦合強度0.5≤Γ≤1.5所對應的類氦鋁離子的電子溫度隨電子密度的變化數據和曲線. 從圖1中可以看出：在整個電子密度區間，電子溫度隨著耦合強度的增大而減小，這是由耦合強度與電子溫度呈反比所導致的. 當耦合強度為某一定值時，電子溫度隨著電子密度的增加而緩慢升高；這是因為耦合強度等于離子間的庫侖勢能與動能的比值，隨著電子密度的增加，離子間的庫侖勢能則不斷增大，故相應的離子動能必然增大，則電子溫度不斷升高.

圖1 不同耦合強度所對應的電子溫度隨電子密度的變化. Fig.1 The variations of electron temperature versus electron density corresponding to different coupling strengths.

3.2 1s2p (1P1)原子態的能級移動

表2和表3分別所示的是用德拜模型和自洽場離子球模型所計算的不同耦合強度下類氦鋁離子1s2p (1P1)原子態的能級移動量，相應的變化曲線見圖2和圖3. 從圖2和圖3中均可以看出：能級移動量隨著耦合強度的增大而增大；這是因為隨著耦合強度的增大，等離子體的屏蔽效應逐漸增強所致. 從圖2和圖3中還可以看出：當耦合強度為一定值時，能級移動量隨著電子密度的增加而增大；這是因為當耦合強度為一定值時，隨著電子密度的增加，電子溫度也逐漸升高，但是等離子體的屏蔽效應主要取決于電子密度，電子溫度的影響相對較小，故能級移動量隨著電子密度的升高而增大. 從圖3中可以看出：基于自洽場離子球模型所計算的能級移動量隨著耦合強度的減小而逐漸接近于均勻電子氣離子球模型的結果，這是因為隨著耦合強度的減小，對應的電子溫度逐漸升高，電子的空間分布越來越均勻，自洽場離子球模型的有效核勢逐漸趨于均勻電子氣離子球模型的有效核勢，從而引起的能級移動量也逐漸趨于均勻電子氣離子球模型的能級移動量.

表1 不同耦合強度所對應的電子密度nf(cm-3)和電子溫度Te(eV)，數字0.5、0.6……1.4、1.5分別表示耦合強度的大小，R0表示離子球半徑( a.u.).

Table 1 The electron densitiesnf(cm-3) and electron temperaturesTe(eV) corresponding to different coupling strengths, and the figures 0.5, 0.6 … 1.4, 1.5 represent the values of the coupling strengths, andR0represents the ion sphere radius (a.u.).

R0nf0.50.60.70.80.911.11.21.31.41.512.10121.0(22)5444533883403022722472262091941817.07685.0(22)9307756645815164654223873573323105.61691.0(23)11729768377326515855324884504183903.28485.0(23)2004167014311253111310029118357717156682.80898.0(23)23441953167414651302117210659769018377812.60841.0(24)252421031803157714021262114710519719018412.45461.2(24)2682223519161676149013411219111710319588942.27871.5(24)28892408206418061605144513131204111110329632.14321.8(24)307225602190192017071536139612801181109710242.06962.0(24)318126512272198817671591144613251223113610602.00472.2(24)32842737234620531825164214931368126311731095

表2 用德拜模型所計算的不同耦合強度下類氦鋁離子1s2p (1P1)原子態的能級移動量(cm-1).

Table 2 The energy level shifts (cm-1) under different coupling strengths of 1s2p (1P1) atomic states for the He-like Al ions are calculated by the Debye model.

nf0.50.60.70.80.91.01.11.21.31.41.51.0(22)3914695476257037808599381014109211705.0(22)113813651592181820452268249727212948316833901.0(23)180221612518287632313592394642984657500953655.0(23)522262537283830493321035011367123841339314423154198.0(23)71178521991911301126921407615464168481823219597209731.0(24)824698701148513093146981629817900195022108522687242681.2(24)9286111131293114738165431834520143219432374225509272911.5(24)10751128611496417050191422121623302253632744629494315541.8(24)12123145021690319221215682391526257285793092433230355362.0(24)12993155401807920597231162561328120306233312135589380702.2(24)1383616547192462192324599272752992932594352413787040491

圖4對不同耦合強度下基于德拜模型和自洽場離子球模型所計算的類氦鋁離子1s2p(1P1)原子態的能級移動量進行了比較. 從圖中可以看出：當電子密度小于1.0×1023cm-3時，不同耦合強度下德拜模型和自洽場離子球模型所計算的能級移動量幾乎是相同的. 但當電子密度大于1.0×1023cm-3時，隨著耦合強度的增大，用德拜模型所計算的能級移動量由小于自洽場離子球模型所計算的能級移動量，逐漸轉變為大于自洽場離子球模型所計算的能量移動量；當耦合強度Γ=1.1、1.2時，兩個模型所計算的能級移動量符合得很好；當耦合強度Γ>1.2時，德拜模型所計算的能級移動量大于自洽場離子球模型的能級移動量，但二者的差值相對較小. 總之，對于1s2p(1P1)原子態，當耦合強度的值在1.0附近時，德拜模型和自洽場離子球模型所描述的等離子體屏蔽程度是相當的，二者都是適用的.

表3 用自洽場離子球模型所計算的不同耦合強度下類氦鋁離子1s2p(1P1)原子態的能級移動量(cm-1)，UEGM表示用均勻電子氣離子球模型所計算的能級移動量.

Table 3 The energy level shifts (cm-1) under different coupling strengths of 1s2p (1P1) atomic states for the He-like Al ions are calculated by the self-consistent-field-ion-sphere-model, and UEGM represents the energy level shifts calculated by the uniform-electron-gas-ion-sphere-model.

nfUEGM0.50.60.70.80.91.01.11.21.31.41.51.0(22)1202232362482592702802903673073163245.0(22)6389549981079107811151149118412161247127613051.0(23)1286180018731981200620682128218522392292234323935.0(23)64858012827584969005923994629616975396499899100688.0(23)1037412453127691306813835139821422714454146611485015096153381.0(24)1291515270156311605216798171191741817696178891811818412187771.2(24)1539217962184621893520139205412091820831210742128421692220231.5(24)1886921843223582294124348248262527325637260292570226098265691.8(24)2197425138257542637427430278962838228782291452955130006304512.0(24)2374926951275772822729374299343040630845312503162132113325942.2(24)253152840929138298323097931524320323256033001334043392834440

圖2 基于德拜模型所計算的類氦鋁離子1s2p(1P1)原子態的能級移動量隨電子密度和耦合強度的變化. Fig.2 The energy level shifts calculated by the Debye model of 1s2p(1P1) atomic states for the He-like Al ions change with the electron densities and coupling strengths.

圖3 基于自洽場離子球模型所計算的類氦鋁離子1s2p(1P1)原子態的能級移動量隨電子密度和耦合強度的變化. Fig.3 The energy level shifts calculated by the self-consistent-field-ion-sphere-model of 1s2p(1P1) atomic states for the He-like Al ions change with the electron densities and coupling strengths.

圖4 基于德拜模型和自洽場離子球模型所計算的類氦鋁離子1s2p(1P1)原子態的能級移動量的比較Fig.4 Comparison of the energy level shifts calculated by the Debye model of 1s2p(1P1) atomic states for the He-like Al ions with those by the self-consistent-field-ion-sphere-model.

3.3 1s3p(1P1)原子態的能級移動

表4和表5分別所示的是用德拜模型和自洽場離子球模型所計算的不同耦合強度下類氦鋁離子1s3p (1P1)原子態的能級移動量，相應的變化曲線見圖5和圖6. 從圖5和圖6中均可以看出：對于1s3p (1P1)原子態，其能級移動量隨耦合強度的變化趨勢與1s2p (1P1)原子態的相似，即也隨著耦合強度的增大而增大，當耦合強度為一定值時，能級移動量隨著電子密度的增加而增大；基于自洽場離子球模型所計算的能級移動量隨著耦合強度的減小而逐漸接近于均勻電子氣離子球模型的結果.

當耦合強度為1.0時，圖7對采用德拜模型和自洽場離子球模型所計算的類氦鋁離子1s3p(1P1)原子態的能級移動量隨電子密度的變化趨勢做了比較. 從圖中可以看出：當電子密度小于1.0×1023cm-3時，德拜模型和自洽場離子球模型所計算的能級移動量互相符合得很好；但當電子密度大于1.0×1023cm-3時，德拜模型所計算的能級移動量始終小于自洽場離子球模型所計算的能級移動量，且隨著電子密度的升高，二者的差值逐漸增大. 另外，當耦合強度在Γ=0.5～1.5(Γ≠1.0)區間時，德拜模型和自洽場離子球模型所計算的能級移動量隨電子密度的變化趨勢與Γ=1.0的完全相似，故不再贅述. 總之，對于1s3p(1P1)原子態，當耦合強度的值在1.0附近且電子密度小于1.0×1023cm-3時，德拜模型和自洽場離子球模型所描述的等離子體屏蔽強度是相當的；但當電子密度大于1.0×1023cm-3時，德拜模型所描述的等離子體屏蔽強度偏低，須用自洽場離子球模型描述等離子體的屏蔽效應.

表4 用德拜模型所計算的不同耦合強度下類氦鋁離子1s3p (1P1)原子態的能級移動量(cm-1).

Table 4 The energy level shifts (cm-1) under different coupling strengths of 1s3p (1P1) atomic states for the He-like Al ions are calculated by the Debye model.

nf0.50.60.70.80.91.01.11.21.31.41.51.0(22)120714471688192521652402264228853117335635945.0(22)3498418948815569626069367631831089959660103331.0(23)552166137693877898501094012008130691414815208162755.0(23)15846189352201425054281133113134143371494012743161460898.0(23)21517257012985433925380374211446198502575433658326623381.0(24)24882297113449539218439454864553340580246266567329719261.2(24)27977333933876344063493655464259895651417039875526806891.5(24)32322385584475250850569726302569096750808113587057929961.8(24)363784339250444572036404970877776718438991183978251044502.0(24)3894646444538886121868553758058306190291975101046031117182.2(24)4143349398573006508272862806188828995970103604111145118647

表5 用自洽場離子球模型所計算的不同耦合強度下類氦鋁離子1s3p(1P1)原子態的能級移動量(cm-1)，UEGM表示用均勻電子氣離子球模型所計算的能級移動量.

Table 5 The energy level shifts (cm-1) under different coupling strengths of 1s3p (1P1) atomic states for the He-like Al ions are calculated by the self-consistent-field-ion-sphere-model, and UEGM represents the energy level shifts calculated by the uniform-electron-gas-model.

nfUEGM0.50.60.70.80.91.01.11.21.31.41.51.0(22)789128413481407146415181568161817341710175417975.0(22)4162560558146052620063816551671968787033718073241.0(23)839810690110331139611668119631225212526127901304913297135415.0(23)4312749610506695165452807537485464855462562385685257720584738.0(23)7027178958803508168283728845368571186842879318897390044911001.0(24)88907988261004261020331039121053391067091080341092481104541117181130181.2(24)1081521191771210641228691252201268591284381296631310561323821338631352541.5(24)1380971507691528831550031577281596401614711631951648981660451676901693901.8(24)1698061838721862901886701913451934361955051974511993112011892030602048902.0(24)1915922064852090472115612144652167732189392210422230732250182270322290132.2(24)214414230012232807235493238509240928243263245562247742249830251993254099

圖6 基于自洽場離子球模型所計算的類氦鋁離子1s3p(1P1)原子態的能級移動量隨電子密度和耦合強度的變化. Fig.6 The energy level shifts calculated by the self-consistent-field-ion-sphere-model of 1s3p(1P1) atomic states for the He-like Al ions change with the electron densities and coupling strengths.

圖7 當耦合強度為1.0時，采用德拜模型和自洽場離子球模型所計算的類氦鋁離子1s3p(1P1)原子態的能級移動量的比較. Fig.7 Comparison of the energy level shifts calculated by the Debye model of 1s3p(1P1) atomic states for the He-like Al ions with those by the self-consistent-field-ion-sphere-model, when the coupling strength is equal to 1.0.

4 結 論

本文分別采用德拜模型和自洽場離子球模型計算了類氦鋁離子1snp [n=2-3] (1P1)原子態的能級移動量隨電子密度的變化規律，并對二者所計算的能級移動量進行了比較. 結果表明：能級移動量隨著耦合強度的增大而增大；當耦合強度為一定值時，能級移動量隨著電子密度的升高而增大；基于自洽場離子球模型所計算的能級移動量隨著耦合強度的減小而逐漸接近于均勻電子氣離子球模型的結果. 當電子密度小于1.0×1023cm-3時，不同耦合強度下自洽場離子球模型和德拜模型所計算的能級移動量幾乎是相同的. 對于1s2p (1P1)原子態而言，當電子密度大于1.0×1023cm-3時，隨著耦合強度的增大，用德拜模型所計算的能級移動量由小于自洽場離子球模型所計算的能級移動量，逐漸轉變為大于自洽場離子球模型所計算的能量移動量；當耦合強度Γ=1.1、1.2時，這兩個模型所計算的能級移動量符合得很好；當耦合強度Γ>1.2時，德拜模型所計算的能級移動量大于離子球模型的能級移動量，但二者的差值相對較小. 對于1s3p (1P1)原子態而言，當電子密度大于1.0×1023cm-3時，德拜模型所計算的能級移動量始終小于自洽場離子球模型所計算的能級移動量，且隨著電子密度的升高，二者的差值逐漸增大.

總之，對于等離子體中的類氦鋁離子的1s2p(1P1)原子態，當耦合強度的值在1.0附近時，德拜模型和自洽場離子球模型所描述的等離子體屏蔽程度是相當的，二者都是適用的. 對于1s3p(1P1)原子態，當耦合強度的值在1.0附近且電子密度小于1.0×1023cm-3時，德拜模型和自洽場離子球模型所描述的等離子體屏蔽強度是相近的；但當電子密度大于1.0×1023cm-3時，德拜模型所描述的等離子體屏蔽強度偏低；因此，對于1s3p(1P1)原子態，須用自洽場離子球模型描述等離子體的屏蔽效應.