基于市場需求的共享單車優化調度研究

□文/趙 婷 廖成林

（重慶大學經濟與工商管理學院 重慶）

［提要］ 共享單車的出現切實解決了“最后一公里”的難題，因此建立優化調度模型以提升共享單車的服務效率，保證共享單車的最大使用率具有重要意義。本文以用戶需求為前提，以共享單車調度產生的費用以及未被調度產生的損失的最小為目標函數建立優化調度模型。運用改進的遺傳算法對包含25個共享單車需求站點的算例進行求解，分析計算后得出該區域共享單車的優化調度方案和最小調度成本，表明該模型在共享單車調度問題上具有一定的可行性。

引言

共享單車作為共享經濟時代下最典型的產物，并作為中國新世紀“新四大發明”之一走向世界，它切實解決了“最后一公里”的問題，為人們的出行提供了很大的便利。

相比于傳統的公共自行車，無樁停放，即停即用是共享單車最大的特點，因此各個區域共享單車的數量是一個動態平衡的狀態，但是受到用車需求的潮汐變化過程，在高校、居民樓以及寫字樓等區域的位置共享單車并不能保證自平衡狀態，因此根據各個區域的潮汐用車需求對共享單車進行周期化的優化調度，對保證共享單車最大的使用限度，保證最大化利益具有重要的作用。

共享單車的調度可以看作為調度車輛的路徑問題（Vehicle Routing Problem，VRP），而共享單車的調度又可以分為動態調度和靜態調度。汪慎文等人考慮了共享單車的初始數量和共享單車數量的變化率，建立了共享單車的動態調度模型。趙敬洋等人運用分時段調度思路把自行車系統的調度時間劃分成多個連續的調度周期，從而將動態調度問題靜態化。Lin J等人研究單車調度時建立了一個非線性的整數規劃模型。ContardoC則以調度站點對自行車的需求最小為目標函數建立了優化調度模型，用于對各個調度站點的自行車輛進行調配。ChemlaD在研究自行車調度時將其簡化為單配送車輛的調度，并以總調度距離最小為目標函數建立模型，對實現共享單車的復雜調度問題實用性較低。楊珈惠等人研究共享單車的調度時可以允許調度車輛的局部重復路徑，當前研究主要以最少運輸費用為調度模型的目標函數，Benchimol M等人假設調度恰好滿足所有站點的需求，并以最小的調度費用為目標函數建立靜態調度模型進行求解。目前對于自行車的優化調度模型已經有相當一部分成果，但是少有同時考慮當調度車輛過多或者過少帶來的損失費用。因此，本文提出了一種基于用戶需要的共享單車調度模型，該模型以共享單車調度產生的費用以及未被使用產生的損失費用最小值為目標函數建立優化調度模型，能夠很好地滿足目前共享單車調度方案的需求。

一、共享單車需求模型

為了得到某區域共享單車的投放量，需要根據該區域對共享單車的需求進行分析，本文基于該地區的人口數量及人口結構為基礎，通過分析不同層次人口對于車輛的使用頻次，從而得到該年齡層的用車率。根據共享單車的需要，對某局部區域的人口結構和職業可以做劃分，如表1所示。（表1）

根據表1中年齡和職業劃分的五種結構，假定在某個調度區域中第i個年齡段的人數為Ri，該年齡層單日使用共享單車的概率為ui，則可以得到該區域共享單車的需求量為：

針對某個包含j個調度區域的地區，則該地區共享單車的需求量可以表示為：

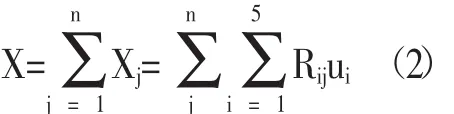
其中，Cj表示第j個區域中共享單車的需求量；Rij表示第j個調度區域內第i個年齡段人口的數量。

二、共享單車優化調度模型

共享單車的調度受其運營方式的影響，使得其調度過程是一個復雜的動態過程。通常，在對共享單車進行調度分析時，我們把它的調度過程簡化成靜態過程。本文在建立優化調度模型時，考慮調度的目標函數為如下兩個部分：（1）考慮調度過程中由于調度運輸產生的費用；（2）某個待調度區域共享單車過少或者過剩時由于未被使用帶來相應的損失費用。假設待調度區域只包含一個調度中心（用坐標（0，0）表示調度中心），從該調度中心出發，m輛調度車輛對n個調度區域進行調度時，則調度費用可以表示為式（3）所示：

表1 某區域人群職業與年齡結構劃分一覽表

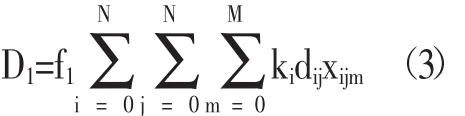
其中，f1表示1km的運輸成本（單位：元/km）；dij表示從調度點i到調度點j的距離（單位：km）；

同時，需要保證從調度中心出發的調度車輛，經過調度之后最終需要回到調度中心，且進入某調度站點的車輛調度完成后，必須從該調度站點出發進入下一個調度站點或者直接回到調度中心，因此可以表示為：

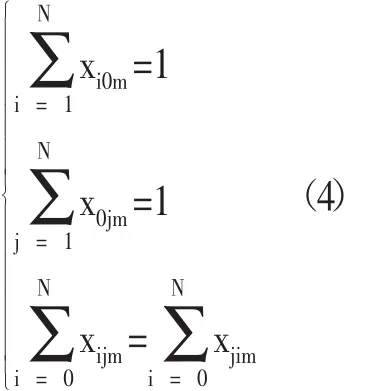
為了簡化調度問題，設定每個共享單車調度站點的調度任務最多只由一輛車負責，如果被調度只允許被調度一次，則有：

其中，yim表示，第i個調度站點是否有第m輛車完成。

此外，當某個區域的共享單車超過其實際需求時，會導致該地區共享單車空置浪費；當某區域數量較少時，則無法滿足該區域用戶的需求時，又會導致損失。因此，考慮當第i個站點未被調度時，由于未調度所產生的損失費用可以表示為：

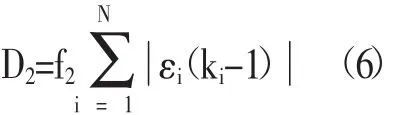
其中，f2表示一輛單車每天產生的平均收益（單位：元）。

當某個站點被調度之后，但仍未完全達到調度站點的需求，假設調度過程中對第i個站調度單車數量為φi，則也會產生一部分損失費用，可以表示為：

其中，εi表示第i個調度站點自行車的需求量，當εi＞0時表示該站點需要車輛，當εi＞0時表示該站點車輛過多，需要調走；φi表示第i個站點的實際調度量。

根據上述分析，本文針對共享單車的優化調度模型提出如下假設：

（1）假設該區域共享單車總數保持不變；

（2）假設共享單車的調度為靜態調度，每天的調度均在夜間進行；

（3）假設在一個小范圍內的共享單車需求量可以通過一個調度站點滿足；

（4）調度過程中人力成本與車輛運輸成本統一結算為運輸成本；

（5）忽略由于共享單車丟失和破損帶來的損失。

基于上述假設，本文以共享單車調度產生的成本費用與未被調度時產生的損失費用的和的最小值為目標函數，建立共享單車優化調度模型：

通過建立的上述模型，我們可以得到某地區單個調度中心情況下的共享單車優化調度策略，并保證最優的成本和最低的損失費用。

三、算例分析

（一）初始化調度信息。本文首先在某區域中的二維坐標隨機生成共享單車用戶的位置信息以及對應的需求數量，并將該區域均衡的分為25個調度區域，根據用戶的需求信息以及調度區域的位置信息，并運用重心法求出每個調度區域的調度站點，保證每次調度車輛將共享單車調度在該位置可以滿足調度需求。最后，初始化各個調度站點的需求數量如表2所示。（表2）

其中，表2中需求量的正負表示了該調度站點是否需要調度共享單車，正值表示該站點需求為正值，需要由其他站點調配過來，而負值則表示需要由該點向其他地方調配。

（二）調度參數設置

1、調度站點的距離。在已知各個調度站點的坐標的前提下，為了簡化問題，本文選取兩個調度站點的歐式距離作為兩個站點之間的調度距離。

2、共享單車的調度和損失費用。共享單車的調度費用作為本文調度模型的目標函數，共享單車的運輸費用和損失費用都將極大影響調度方案和策略，針對現有共享單車的收費標準加上用車情況，本文對調度費用作如下假設：針對該區域，共享單車的調度運輸費用為12元/km，而當共享單車不滿足用戶需求或者是超過用戶需求，所帶來的損失費用為8元/輛·天。

3、調度車輛信息。本文假定上述劃分的25個調度站點（分別命名為1-26號），均由該區域的調度中心負責調度，該調度中心包含三輛調度車，每輛車最大裝載量為40輛共享單車。

（三）調度方案計算。目前，運用遺傳算法求解物流配送車輛路徑問題（VRP）問題的研究具有較多成果，運用遺傳算法對該優化的調度模型進行求解，求解步驟如下：

1、參數初始化：初始化樣本個數N，最大迭代次數n，交叉概率pi和變異概率pm。

2、種群初始化及編碼：本文將調度站點隨機連接遍歷的路徑作為初始化種群，并通過自然編碼的方式對該初始化種群進去編碼為 E（1，2，3，…，m）。

3、適應度函數：計算本次迭代種群的最優適應值。

4、迭代：判斷是否到達最大迭代次數n，如果到達則退出循環并輸出最優的適應值，否則進入（5）。

5、交叉和變異：選擇（4）中個體適應度值小的作為優良的染色體，并按照設置的交叉變異概率進行交叉變異操作，產生新的種群并轉入（3）繼續計算適應值。

6、迭代終止：到達最大迭代次數，選擇最小的適應值作為最優的調度費用，并輸出對應的調度路線。

設定遺傳算法迭代的參數如下：以模型的目標函數作為迭代的適應度函數，初始化樣本為2，000個，交叉概率設為0.9，變異概率設為0.12，終止迭代次數為600代。

本文分別計算派出1、2、3輛車的情況進行調度方案計算，并且保證所派出的調度車輛都需要有調度任務，通過MATLAB編程進行計算，得到三種調度情況的最優調度路線和最小的調度費用如表3所示。（表3）

從表 3 可以看出，1 輛車調度時，站點 7、12、19、22、24 未被調度，而其他站點被調度且滿足站點的車輛需求，最優的調度費用約為551.19元；當我們使用2輛調度時，其費用為477.14元，其中 4、7、10、12、19、21、26這 7 個站點未被調度，當使用3輛車進行調度且保證都有調度任務時，其調度費用反而增加，最優調度費用為600.78元。分析發現，相比于1輛車和3輛車，派出2輛車時其服務的站點較少，但是節省了調度運輸費用，保證了綜合成本最小。

表2 共享單車各個調度站點的位置坐標和投放自行車數量一覽表

表3 共享單車最優調度路徑一覽表

四、結論

本文結合共享單車無樁停放的特點，深入分析了影響共享單車調度的因素，運用旅行商問題的相關研究結果，根據當前區域對共享單車的需求情況，建立了以調度運輸費用和共享單車未被調度所造成的損失最小為目標函數的優化調度模型。通過改進的遺傳算法對該模型進行求解，對包含25個調度站點的區域進行計算，得到在不同數量調度車輛的情況下的調度方案和調度費用，得到了最優調度方案。通過模型可以得出，本文提出的考慮共享單車損失費用的調度模型完善了傳統調度模型的不足，在很好地解決了共享單車調度的同時，保證了共享單車企業的利益更大化，對共享單車的優化調度方案具有一定的參考價值。