利用擴展的簡單方程法求解時空分數階偏微分方程

趙云梅，楊云杰

（1.紅河學院數學學院，云南蒙自 661199; 2.昆明學院數學系,昆明 650214）

1 引言

由于分數階導數是非局部算子，對它進行刻畫時依賴于初始時刻的歷史狀態，因此分數階模型比整數階模型在描述某些現象和反映物體的某些性質時更精確，物理意義更清晰，表述更簡潔，它已經成為復雜力學與物理工程數學建模的重要工具之一，已被廣泛地應用到粘彈性阻尼器、流體力學[1]、生物醫學工程、圖像處理[2]、信號處理和系統識別、振動與控制[3]、地震分析[4]等領域。目前分數階微分方程已成為數學、物理、醫學和經濟等領域的研究熱點。

分數階非線性偏微分方程并不是整數階非線性偏微分方程的平行推廣，許多整數階微積分的性質在分數階微積分中不一定成立，若是要獲得分數階微分方程的精確解就變得很困難。盡管求解分數階偏微分方程的精確解較為困難，但是分數階微積分是由整數階微積分引出的，在求其精確解時，可以針對不同方程的特征，探索并構造相應的求解方法是可以實現的。目前國內外學者提出和發展了一些求解方法，如：分數階子方程法[5-6]、分數階Riccati展開法[7]、分數階(G'/G)-展開法[8-10]、變量分離法[11]、簡單方程法[12]、分數階Jacobi橢圓方程法[13]和分數階首次積分法[14]等。

簡單方程法和擴展的簡單方程法[15]是求解整數階微分方程非常有效的一種方法，廣大學者運用該方法獲得了許多整數階微分方程的精確解。本研究利用分數階復變換和擴展的簡單方程相結合，提出一種求解分數階微分方程精確解的新方法，該方法直觀、簡單有效。

2 預備知識

整合分數階導數：

設的階導數的定義為：

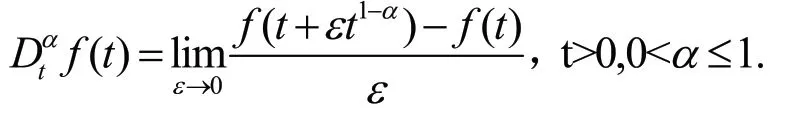
具有如下性質：

設在時可微，則有

3 方法簡述

考慮如下分數階微分方程：

其中是待求函數關于自變量和的分數階導數，是關于函數及其偏導數的多項式。

為求解方程①的精確解，引入一個復變換：

其中為待定常數，把②代入①式得：

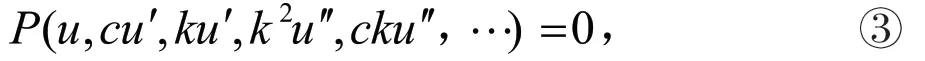
假設式③的解可以表示為如下形式：

其中為待定常數，且，正整數通過平衡③式中的最高階導數項和非線性項來確定，滿足：

其中為常數，由文獻[15]知方程⑤的解為：

把④代入③式，利用⑤和⑦，③的左邊就可以化為關于的多項式，令它們的各次冪系數為零，便得到一組關于待定常數的代數方程組，求解該方程組得到相關常數，最后代入④式，便求出方程①的精確解。

4 應用

下面考慮一個脈沖時空分數階非線性微分方程[16]

2018年,文獻[17]用擴展的函數法和廣義的Kudryashov方法探討該方程，得到了一些精確解，下面將用上述方法求解該方程。

把復變換②代入⑧可得：

平衡⑩中最高階導數項和非線性項得，可得即

其中為待定常數，把?代入⑩式結合⑤和⑦，⑩的左邊就可以化為一個關于和的多項式，令它們的各次冪系數為零，便得到一組關于和的代數方程組，利用Maple求解該方程組得如下解：

（1）

把?、? 代入?，可得方程⑧的精確解：

5 部分精確解的波形圖

圖1 的二維波形圖

圖2 的二維波形圖

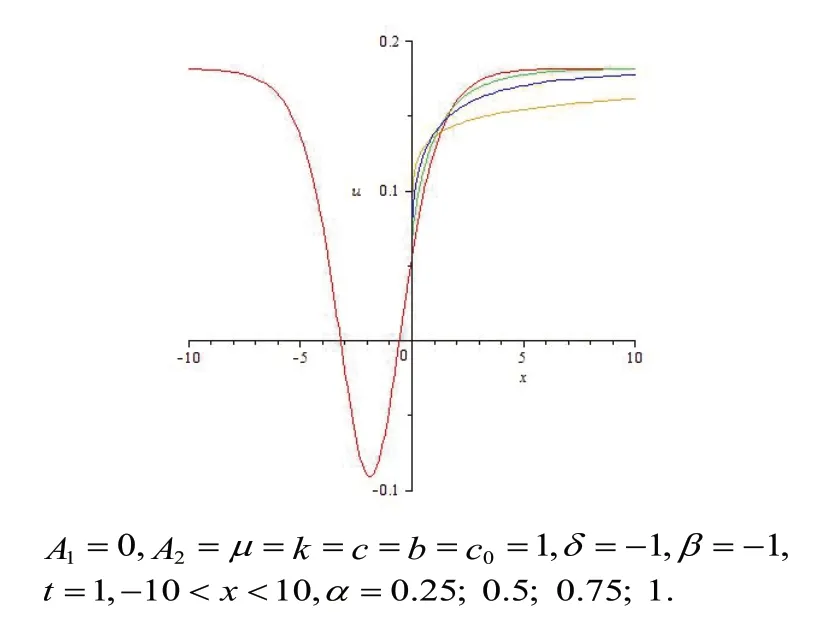
圖3 的二維波形圖

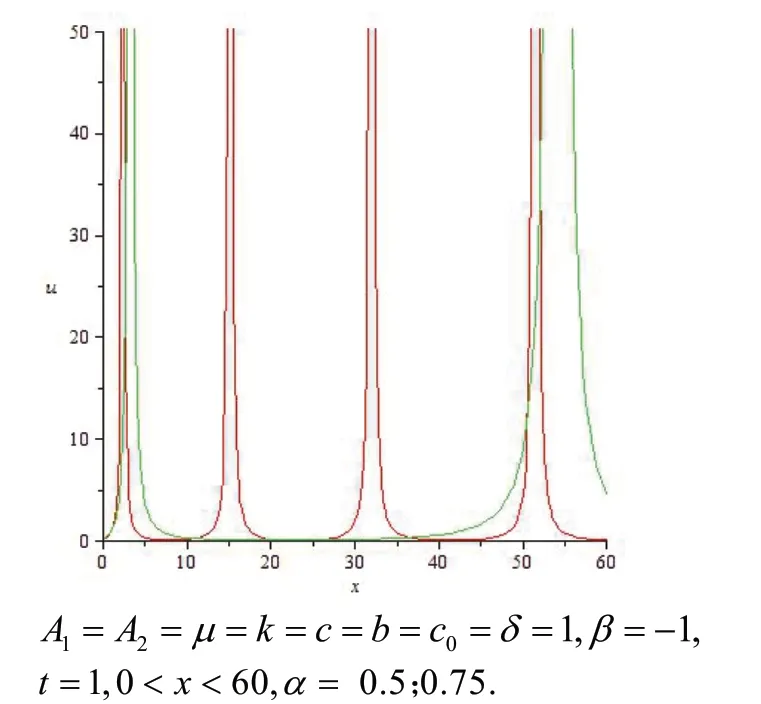
圖4 的二維波形圖

6 結論

本文把分數階復變換和擴展的簡單方程法相結合，提出了一種求解時空分數階非線性微分方程精確解的新方法，為了展示該方法的實效性，運用該方法求解了一個脈沖時空分數階非線性微分方程，獲得了該方程的許多用雙曲函數、三角函數和有理函數等表示的精確行波解，并運用數學軟件Maple繪出部分精確解在不同參數、取不同值的二維波形圖，這對我們進一步理解復雜的非線性物理現象和分數階微分方程的原理具有一定的幫助。本文中提出的方法在求解時空分數階微分方程精確解時具有簡潔、直觀、有效的特點，也可以推廣到求時間分數階、空間分數階微分方程的精確解。