淺談指向深度學習的數學概念教學

丁靜

摘要：在數學概念教學中，教師采取適當的教學策略，重視數學概念的引入方法，注重概念的形成過程，加強概念的遷移應用，可以促進學生深度學習，有效地提高學生的綜合素養和思維品質。

關鍵詞：數學概念教學;深度學習

中圖分類號：G633.6 文獻標識碼：A文章編號：1992-7711（2020）23-035

數學概念是反映數學對象的本質屬性和特征的思維形式。如果學生沒有學好數學概念，那么對數學公式、定理和方法就不可能理解，就不能順利開展數學學習，最終也不能促進學生數學思維的發展，達到深度學習。那么，如何在數學概念教學中開展深度學習，培養學生的核心素養呢？

一、巧引入，趣化概念教學的序章

概念引入是概念教學的第一步，也是概念形成的基礎。概念教學中要引導學生經歷從具體的實例抽象出數學概念的過程。在引入中創設各種情境，給予學生學習體驗。沉浸體驗式學習是深度學習的重要學習方式。下面介紹幾種引入數學概念的方法：

1.創設問題情境引入新概念

我們可以創設具有趣味性，探索性的問題情境，激發學生概念學習的興趣，使學生在對問題的分析中，歸納和抽象出概念的本質特征。

例如：在講解等可能性概念時。由于概念比較長，為幫助學生理解，我們可以引入這樣的問題情境。江蘇省乒乓球比賽在市體育館舉行，我校每班發到一張入場券，現在我班有兩名同學小盧和小錢為此名額爭得面紅耳赤，你能為他們支招嗎？從現實出發，因為當時上這節課的時候市體育館正在舉行江蘇省乒乓球比賽，所以問題一出來，就吸引學生，學生積極投入出主意，有的說拋硬幣，拋圖釘，抽簽，擲骰子，通過不同的主意幫助學生歸納出事件發生等可能的概念。

2.創設虛擬情境引入新概念

運用人工智能、三維動畫、模擬仿真等技術，構建一個集聲音、畫面、場景、人物（角色）等要素于一體的體驗式虛擬學習空間。

例如講解勾股定理時，可以利用多媒體為學生展示勾股樹，引導學生在觀看動畫過程中發現數學的美，增強了學習數學的欲望。

3.從實際生活中引入新概念

引入數學概念要根據概念類型，以具體的典型材料和實例為基礎，創設情境，幫助學生完成由感知材料到理性認識的過渡。

例如：在講解三角形概念時，我們可以列舉生活中含有三角形的實物，大到宏偉的建筑物，高樓大廈，飛機機翼，小到分子結構，使學生經歷從現實世界中抽象出幾何模型的過程。

4.用類比的方法引入新概念

類比不僅是思維的一種重要形式，也是引入新概念的一種重要方法。對于相關的概念要進行類比、分析，弄清內在聯系，歸納出概念的本質特征。

例如：由電影票上都標有“第x排第y座”的字樣，得出“用一對有序實數確定點的位置”，由“溫度計”引導學生認識“數軸”，用“分數”類比“分式”等概念的教學，都可以通過類比引入。

5.介紹數學史引入新概念

知識只有通過情感體驗融入學習者的心理結構，內化為學習者的心理結構，再內化為學習者的情感、態度和價值觀，才能實現其最大價值概念的形成。

例如在“平面直角坐標系”教學中，教師可與學生分享著名數學家笛卡爾的故事：笛卡爾在夢中觀察一只蜘蛛結網，然后由其結網的距離、運動軌跡等規律發明了平面直角坐標系。學生在此過程中會因故事的有趣而產生對平面直角坐標系這個知識點的濃烈興趣，繼而會迫切地想知道由蜘蛛結網啟發而生成的數學知識是何種形式。這樣教師便有效地激發了學生對數學概念的學習興趣。

以上介紹了5種引入概念的方法，當然還有其他的方法，比如利用學具，操作體驗等方法，不管是何種方法，我們都要創設情境讓學生體驗。體驗是深度學習的本質使然。深度學習需要情境體驗。在概念教學中要創設各種情境，引導學生求知的欲望。

二、重過程，強化概念的形成過程

1.把概念的生成過程問題化

問題是數學活動的心臟。問題探究式學習是深度學習的重要學習方式。將數學概念的形成過程、形式化的數學概念及一些相關的材料轉化為富有生活意義的問題，形成問題情境，從而把學生帶入問題中。在問題探究中“學數學、做數學、用數學”，使概念學習變為學生的內在需求。

例如：在引出圓的集合的定義時，可以設計問題1.生活中離不開圓，你能解釋為什么車輪做成圓形的呢？后續再設計追問，歸納得出圓上各點到定點的距離都等于定長這個結論;再設計問題2.同學們在玩投圈游戲時，如何站游戲才公平？幫助學生體會：到定點的距離都等于定長的點都在同一個圓上這個結論。通過這兩個問題的探究和分析，將學生的生活經驗轉化為數學認知，學生在充分理解的基礎上形成圓的集合定義就非常自然了。

2.把握概念的內涵和外延

概念的內涵就是反映在概念中的對象的本質屬性，它說明概念反映的事物是什么樣的。概念的外延是指具有概念所反映的本質屬性的對象，它說明概念所反映的是哪些事物。它反映的是概念的量的方面。

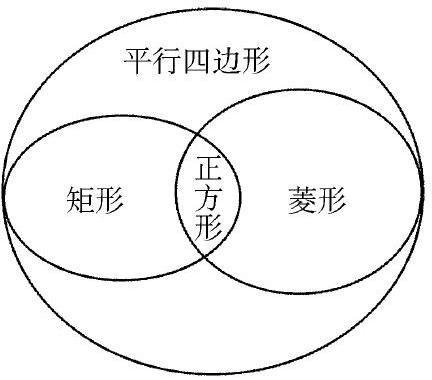
例如：“平行四邊形”的內涵是“兩組對邊分別平行”，它揭示了“平行四邊形”與“四邊形”的隸屬關系，以及它們之間的區別性。其中的關鍵詞“兩組對邊分別平行”，既可以作為平行四邊形的判定方法，又可以是平行四邊形的一個性質;“平行四邊形”的外延是指矩形、菱形、正方形的全體，我們還可以通過表格的形式幫助學生理解概念的內涵和外延，幫助形成一個完整的概念認知地過，既符合學生的認知需要，又體現了概念形成的特點。

3.抓住概念間的聯系和區別

數學概念不是孤立的，而是存在著橫向與縱向的關系。在教學時我們可以把有關的概念串聯起來，充分揭示它們之間的內在規律，啟發學生進行系統歸納，明確概念的聯系和區別。

（1）類比聯想并列相關的概念。例如：二次根式的加減就是合并同類二次根式，它可以與初一的整式加減中的合并同類項類比，使合并同類根式與合并同類項的新舊意義迅速得到同化。在類比中找特點，在聯想中求共性，把數學知識系統化。

（2）對比區別容易混淆的概念。例如：學完“冪的運算”可以把初一下學期的冪的乘除乘方運算和上學期的加減運算放在一起找出他們的區別和聯系。通過對比加深對概念的理解，避免混淆，從而提高學生認知概念的清晰度。

（3）圖表體現從屬關系的概念。以圖表的形式表現出來，便于學生將概念系統化、條理化，有利于記憶和理解。例如：平行四邊形，菱形，矩形，正方形用這張圖表示他們的從屬關系一目了然，進一步加深了對他們之間的聯系和區別的理解。

三、重延展，活化概念的遷移應用

遷移應用是深度學習的重要特征，把新學的知識與已知的概念、原理聯系起來，促進新知識的學習與新技能的形成。布魯姆的教學目標認知維度中把應用、分析、評價、創造歸為遷移，屬于深度學習范疇，深度學習課堂重視知識的遷移。

1.遷移應用，促進問題的有效解決

從深度學習的內涵來看，非常重視學習的遷移應用，要引導學生深入理解概念，通過變式將所學知識運用在新情境中解決問題，達到遷移的目的。

例如：在學習反比例函數k的幾何意義時可設計

問題1.如圖，點A在雙曲線y=6/x上運動，過點A向兩坐標軸作垂線段得矩形ABOC，試判斷矩形ABOC面積的變化情況，并說明理由。

變式1.若點A在第三象限的雙曲線圖像上運動，上述結論成立嗎？

變式2.若修改反比例函數的表達式，上述結論還能成立嗎？

變式3.在問題1中，若連接AO，則△AOB的面積是______________ ，△AOC的面積是 _____________。

變式4.對于y=k/x（k≠0），則△AOB的面積是_____________ ，△AOC的面積是 _____________。

通過精心設計典型性的問題和變式，讓學生通過多層次、多角度的練習，來達到正確理解概念、鞏固概念的目的。深度學習需要學生置身于具體的情境之中提出問題，并通過對比、分析、比較、概括和歸納，以及調研、實驗、問題求解以及創造等學習活動，對于問題作出自己的判斷，從而尋找出解決問題的有效方法。

2.遷移應用，建立新舊知識間的聯系

從深度學習的內涵來看，非常重視學習的遷移應用，要引導學生深入理解概念，通過“數學活動”將所學知識運用在新情境中解決問題，達到遷移的目的。以學生的認知為基礎，充分挖掘概念的內涵，以學生的認知為基礎，不斷豐富概念內涵，在理解概念的基礎上學會遷移與運用。

例如學生結束了一次函數整章的學習后，對函數的認識往往停留在運用規律性結論解決具體問題的層面上，缺乏方法的提煉與能力的提升，可以通過活動幫助學生掌握研究函數問題的一般方法。可設計

活動1.回憶函數y=2x圖像及其性質的探究過程，向學生提問函數的性質在表格和解析式中是否有體現？

活動2.教師分別以圖像、解析式、表格三種不同形式展示三個函數，請學生分別從函數的三種不同表示方法分析函數的性質。

活動3.探究函數y=x+1/x的性質。

活動4.探究函數y=2x3-x的性質。

學生應用函數性質初步探究的一般方法進行合作探究，遷移鞏固所學方法，提升合作交流能力，獲得成功的體驗，達到深度學習。

3.遷移應用，促進學習過程的建構反思

進行反思性的建構是深度學習的重要特征。數學知識之間是存在內在聯系的，提高學生在數學學習中的知識聯結能力是實現深度學習的體現。在教學中，我們可以引導學生反思所學，在數學原理、定義以及法則之間組織起有效的認識結構，從而形成知識網絡，在此過程中實現深度學習。

我們還可以引導學生通過思維導圖的方式梳理各概念之間的聯系和區別，在此反思建構過程中學生對于數學知識的理解得到再認識和再升華，從而形成不同的類別、形態以及性質的知識結構。實現學生對于數學概念認知的擴展和延伸。

走向深度學習是課改的必然要求，也是課改深度的重要標志。在數學概念教學中，我們應采取適當的教學策略，促進學生數學學科知識的認知深度和思維深度，培養學生解決問題的能力、批判性思維能力、自主學習能力、創造性思維能力以及信息素養和協作能力，從而有效地提高學生的綜合素養和思維品質。

（作者單位：太倉市第二中學，江蘇 太倉215400）