在概念復習中提升數學核心素養*

安徽省界首第一中學 (236500) 趙天璽 朱慶斌

一、問題提出

有種很有道理的說法：“平時教學是栽活一棵樹，復習過程是育好一片林.”可見復習課是課堂教學中的重要一環.目前高三數學復習在某一章節或某一單元內容的第一個課時，教師通常會把所有的相關知識進行“梳理”.概念復習主要是放在“知識梳理”這一塊，通常是把概念設計成填空題，讓學生填寫關鍵詞.按照這種教學流程，教師僅把數學概念復習當作概念的簡單再現，況且由于時間倉促，有些數學概念還沒來得及記住就過去了，更談不上對概念的再理解，這樣的概念復習效果可想而知.怎樣做好概念復習，提升學生的核心素養，本文將通過兩道模考題的講評案例，給出筆者的教學思考.

二、教學案例

案例1 已知實數x，y滿足約束條件

師：模考中這道題做錯的同學比較多，現在請做錯的同學說說考試的時候你是怎樣思考的？

生1：一開始看到這道題，以為是個線性規劃題，畫出了可行域，可目標函數不是線性的，不知道如何下手，最后還是沒有做出來.

圖1

師：不對的原因還是你沒有真正理解概念的本質和內涵.現在我們一起梳理一下“斜率”這個概念，什么是直線的斜率？

眾生：斜率是衡量一條直線傾斜程度的量.它通常用傾斜角的正切值，或兩點的縱坐標之差與橫坐標之差的比來表示.

師：那么什么是直線的傾斜角？它的變化范圍是什么？傾斜角取何值時，斜率不存在？

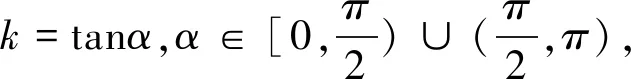
圖2

生4：不是.

師：不錯，我們只能說它有兩個增區間，而在兩個區間的并集上不是單調遞增的，這一點是同學們容易產生錯誤的地方.題目要求點(x,y)和點(1,-2)連線l斜率的取值范圍，是不是應該先把l傾斜角的變化范圍找出來？

圖3

眾生：是的.

師：我們來一起找，如圖3，當點(x,y)位于點C(2,0)時，此時傾斜角是銳角α1，且tanα1=2，點(x,y)向左運動時l的傾斜角變大，點(x,y)位于點B(-1,0)時l的傾斜角α2最大，是鈍角，且tanα2=-1，所以l傾斜角α∈[α1,α2].要求l斜率的取值范圍下一步該怎么做？

師：不錯，現在請生2重新做一遍這個題目.

圖4

綜上y∈(-∞,-1]∪[2,+∞).

師：很好.現在明白考試時做錯的原因了吧？

生2：明白了，我把斜率在區間[α1,α2]上當作單調遞減的了.

師：看來同學們對數學概念特別是像“斜率”這樣的數學核心概念本質和內涵的理解有待進一步地加深.

(1)求曲線C1的普通方程，曲線C2的直角坐標方程;

(2)設直線l：y=x與曲線C2交于M、N兩點，過F(-1,0)作與直線l垂直的直線交C1于P、Q兩點，求四邊形MPNQ面積.

圖5

師：先別急，你怎么知道四邊形MPNQ是個菱形？它的對角線互相垂直平分嗎？

生2：H點不是QP的中點，四邊形MPNQ不是菱形.

師：還有其他求弦長的方法嗎？

生3：求直線與圓相交于的AB時，|AB|=

師：很好，還有其他的方法嗎？

生4：還可以用直線的參數方程來求，具體公式想不起來了.

師：好吧.看來同學們對弦長的求法，掌握的并不全面.弦長實質就是兩點間的距離，現在我們有必要把平面解析幾何中“兩點間的距離”及其相關概念深入梳理一下.

師生一起畫出概念知識導圖(圖6)，按照導圖依次梳理有關概念、公式及方法.

圖6

師：現在請同學們在直角坐標系下，用不同的方法求弦|MN|.

生6：(法二)利用直線與圓相交的弦長公式

師：很好，現在說說極坐標系下怎樣求弦|MN|.

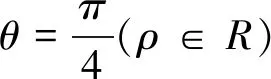
師：上面的四種方法，是否都能用于求弦|PQ|.

眾生：法二不行，因為曲線C1不是圓.

師：是的，請同學們用其他三種方法求弦|PQ|.

其他的學生紛紛表示遇到相同的問題.

師：這樣真的不容易得出結果.怎樣才能不必求出θ1、θ2，就可以求出弦|PQ|.

生10：由公式(5)只要θ2-θ1=0或π，極點在直線PQ上即可.

師：原題目中的極坐標系極點在原點，不在直線PQ上.怎樣建立極坐標系才有利于問題的解決？

眾生：這樣建立的極坐標系來求|PQ|比用公式(3)、(4)簡單多了！

師：簡單是建立在以“兩點間的距離”為核心的概念知識體系全面掌握之上！最后易得SMPNQ=

三、教學思考

1.概念復習要立足于對概念本質的深度理解

2.概念復習要致力于建立相關概念間的內在聯系

學生數學能力不強的主要根源在于沒有掌握數學基本概念及其聯系方式，概念復習要加強概念聯系性的教學，從概念的聯系中尋找解決問題的新思路——解題的靈活性并不來自于“題型+技巧”，而是來自于概念聯系通道的順暢.

案例2中，學生求直線與曲線相交的弦長時，方法單一，思路不暢，運算出錯，其根本原因是概念不清，概念聯系通道不順暢，概念知識體系不完備.其實弦長概念的本質就是兩點間的距離，筆者帶領學生構建知識導圖，復習了由這個概念生產或導出的相關概念，掌握了求弦長的各種方法，構建了以“兩點間的距離”為核心的概念知識體系.高三概念復習要考慮前后概念之間的聯系，打破章節界限,根據概念發生發展的脈絡，不斷重建、重構，充實和完善，溝通相關概念之間的聯系，建立相關概念完備的知識體系.

四、結束語

概念復習是概念教學不可或缺的重要環節，是高三復習的重要內容.概念復習要貫徹于高三復習的各個環節，可以在知識回顧、例題講解、試卷評講中穿插進行.隨著概念復習的推進，學生就會對概念理解越來越本質，對概念知識體系掌握越來越系統，從而促進學生對數學本質的把握，提升學生的核心素養.