2019年全國Ⅲ卷理科15題的多解及推廣*

廣東華南師范大學數(shù)學科學學院 (510631) 蔣紅珠四川內江師范學院數(shù)學與信息科學學院 (641100) 劉成龍四川師范大學數(shù)學科學學院 (610068) 紀定春

一、問題再現(xiàn)

二、問題解決

問題解決常常被看作是能動的、不斷發(fā)展的過程，是數(shù)學思維不斷數(shù)學化的過程，是一個探索、發(fā)現(xiàn)、創(chuàng)新的過程．[1]從不同角度解決問題，有助于學生多角度認識問題，發(fā)展求異思維．

點評：分析1對應的是最簡單的方法，也是最容易想到的辦法，分析2對應的方法有助于深入思考問題．

三、問題推廣

張景中院士指出：“推廣是數(shù)學研究中極其重要的手段之一，數(shù)學自身的發(fā)展在很大程度上依賴于推廣．數(shù)學家總是在已有知識的基礎上，向未知的領域擴展，從實際的概念及問題推廣出各式各樣的新概念、新問題．”[2]

分析1:將問題推廣到一般方程．

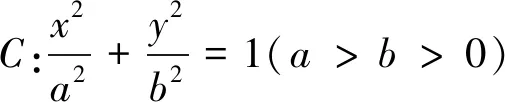
分析2:如果點M為橢圓C上一點且在第二、三、四象限，問題的結果又會怎樣變化呢？

(3)基坑開挖過程中，樁間土體流坍。現(xiàn)場踏勘情況表明，隧道下部地層為中砂，在基坑開挖中有樁間土體流失現(xiàn)象發(fā)生，致使隧道側面及基底地層損失和漏空，進一步影響了隧道結構的受力狀態(tài)。

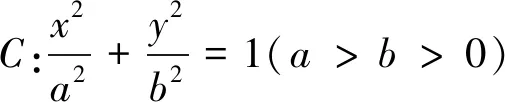
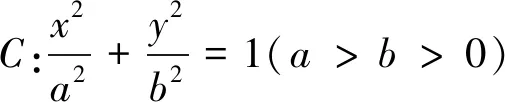
分析3:如果長軸在y軸上，結果又會怎樣變化呢？

分析4:問題的背景為雙曲線，結果又將如何變化呢？

|F1F2|=|MF2|為等腰三角形，則M的縱坐標為

點評：立足成立條件、結構及解決方法將原問題進行推廣，對培養(yǎng)學生發(fā)現(xiàn)問題、提出問題、分析問題和解決問題有積極意義．