一道平幾題的變式與類比

浙江省嵊州中學 (312400) 葉國芳

圖1

題目如圖1,ΔABC的內切圓的圓心為O，BC邊的切點為D，DE為內切圓的直徑，連AE并延長，交BC于F，則BF=DC.

文獻[1]中給出了8種詳盡的解法，其中有平幾法、三角法、解析法等等.本文旨在研究它的變式與類比，將其推廣到圓錐曲線中，并用解析法給予證明，與大家分享.

變式(第十屆中國香港數(shù)學奧林匹克)設F是ΔABC邊BC上一點，且滿足AB+BF=AC+CF，線段AF與ΔABC的內切圓交于點E,Y，且E距點A更近一些，ΔABC的內切圓與邊BC切于點D.證明：(1)DY⊥AF;(2)EF=2OA′，其中O為ΔABC的內心，A′為邊BC的中點.

此變式與原題的條件和結論剛好互換，由原題的結論BF=DC易得BD=CF，于是有AB+BF=AC+CF.其本質是點F為∠A內的旁切圓與邊BC的切點，且點A是∠A內的旁切圓和內切圓的位似中心，E和F是對應點，故過點E的切線與BC平行，從而DE為圓O的直徑，故DY⊥AF.對于第二問，有條件易得BF=DC，而A′為邊BC的中點，故A′為FD的中點，因此EF=2OA′.文獻[2]給出了詳細的解答，此處不再贅述.

類比1 已知有心圓錐曲線W的中心為O，ΔABC的三邊AB、AC、BC所在直線與曲線W都相切，切點分別為P、Q、D，直線DO與曲線W交于點E，直線AE交BC于F，則BF=DC.

證明：設圓錐曲線W的方程為mx2+ny2=1(mn≠0)，A(x0,y0)，P(x1,y1)，Q(x2,y2)，D(s,t)，則E(-s,-t).

由題意，可得切線AB：mx1x+ny1y=1①;切線AC：mx2x+ny2y=1②;切線BC：msx+nty=1③.

又直線AF的方程為(y0+t)(x-x0)-(x0+s)(y-y0)=0,即(y0+t)x-(x0+s)y=tx0-sy0④.

又由①②得PQ的方程為mx0x+ny0y=1.

由題意可知要證|BF|=|DC|，即證|BD|=

化簡⑤式分子(x1+x2)t2-st(y1+y2)-t(x1y2+x2y1)+2sy1y2=(x1+x2)t2-st·

=|DC|.

當m=n>0時，曲線W為圓(如圖1)；當m>0,n>0，且m≠n時，曲線W為橢圓(如圖2)；當mn<0時，曲線W為雙曲線(如圖3)；

圖2 圖3

當把有心圓錐曲線對應為無心圓錐曲線(拋物線)時，直線AF變?yōu)榕cX軸平行的直線，于是可得下面的類比：

類比2 設拋物線W的方程為y2=2px(p>0)，ΔABC的三邊AB、AC、BC所在直線與曲線W都相切，切點分別為P、Q、D，直線AF∥X軸，交BC于F，則|BF|=|DC|.

圖4

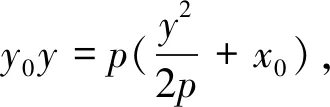
由題意可知:要證|BD|=|CF|，即證xD-xB=xC-xF，即證xD+xF=xC+xB.