轉速大波動下滾動軸承智能故障診斷方法研究

王金瑞 李舜酩 錢巍巍 安增輝 張偉

摘要：機械中普遍存在的轉速大波動工況是影響機械設備故障診斷的關鍵性難題，現有方法在計算效率及診斷誤差等方面存在缺陷。深度學習理論能夠利用深度神經網絡實現數據的自動特征提取和分類。結合深度學習的優勢，提出了一種專門用于處理轉速大波動工況下的智能故障診斷方法。該方法首先根據機械轉速信息提取頻域樣本;然后利用頻域樣本訓練批標準化的深度神經網絡，用批標準化技術中的平移和縮放參數能來處理轉速大波動下頻域信號的頻移和幅變特性，并減輕深度網絡內部協變量轉移問題，加快網絡收斂;最后采用兩組特殊設計的轉速大波動工況下的滾動軸承試驗來驗證提出方法的性能。研究結果表明，該方法可克服轉速大波動的影響，從而實現不同軸承故障的準確識別，并獲得比其他方法更高的準確率。

關鍵詞：故障診斷;滾動軸承;深度學習;轉速大波動;批標準化

中圖分類號：TH165⁺.3;TH133.33文獻標志碼：A 文章編號：1004-4523（2020）02-0391-09

DOI：10.16385/j.cnki.issn.1004-4523.2020.02.020

引言

隨著現代制造業和信息技術的發展，交通、能源、航天等領域的機械設備如高速列車、航空發動機、燃氣輪機等都在朝著復雜化、高速化和智能化發展，因此可靠的健康監測系統也日趨重要。而轉速大波動情況下的健康監測技術尚未成熟，考慮轉速大波動工況的普遍存在：一是由于機械設備啟停產生的大范圍的轉速變化，二是在受載荷、工況的影響下出現的轉速劇烈波動。由此導致信號征兆與故障模式問的映射關系變得異常復雜，給機械設備的健康監測帶來了極大的挑戰。

轉速大波動下機械設備動態信號處理及故障診斷方法的研究開始于2010年，形成的技術路線主要以階次跟蹤及其衍生方法為主。然而在技術可操作性和設備附加成本兩方面都對其發展帶來了阻礙，而且無法達到轉速劇烈和隨機波動下信號分析的精度要求。同時，眾多學者嘗試采用許多相關的非平穩信號分析方法如WVD與cohen類時頻分析、小波變換、故障特征稀疏表示等技術方法。這些方法在設備監測與診斷領域獲得了廣泛應用，但是它們各有自身特點或缺陷，只適合分析某些特定性質的信號。機械設備的動態信號在轉速大波動下具有調幅、調頻、調相等非平穩特征，并且這些特征在時頻域存在強烈耦合。采用以往的時頻分析方法難以有效地解決轉速大波動信號在時頻面內高分辨顯示的問題。一些改進方法或各種方法之問的結合為時頻分析方法表示能力的提升帶來了希望，如基于STFT或小波變換的同步壓縮技術，時頻融合方法以及自適應時頻濾波等技術方法。但它們依然未能完善地解決任意目標高精度的時頻表示，同時也無法實現轉速大波動工況下機械故障的智能診斷。

由于計算機網絡技術的迅猛發展和“大數據”時代的到來，深度學習理論作為一種大數據處理工具，其研究與應用已經取得突破性進展。深度學習已經在圖像、語音識別等領域的大數據分析上取得了長足進步。同時在機械智能故障診斷領域也吸引了廣泛關注：雷亞國等采用對頻域信號加噪的方法設計了五層去噪自動編碼器（DAE），并成功的應用到了多齒輪傳動旋轉部件的故障診斷中。賈峰等建立了五層疊加自動編碼器（SAE）將信號的頻譜特征作為輸入，并對不同負載和轉速下的旋轉軸承故障進行了診斷，診斷準確率幾乎達到100%。趙銳等提出了基于長短時記憶算法（LSTM）的機械健康監測方法，并應用到了機械工具磨損監測中，通過對比發現深度LSTM模型優于淺層模型。Janssens等利用二維CNN對4種不同的旋轉機械故障類型進行了識別，該模型包含一個卷積層和一個連接層，Softmax作為頂部的分類層。

鑒于深度學習強大的表征能力，本文嘗試將深度學習理論運用到轉速大波動下軸承的智能診斷模型的設計中，以實現軸承的智能監測與診斷。同時考慮到轉速大波動下振動頻域信號產生的頻移及幅變特性，使得深度網絡在訓練期問的內部協變量轉移問題加劇，網絡訓練更加困難。考慮在每一網絡激活層中加入一種深度神經網絡優化技術——批標準化算法，其特設的平移和縮放參數可以完美地解決轉速大波動下的頻移及幅變問題;同時通過歸一化每層的輸人來減少內部協變量轉移，并大大地加快深度神經網絡的收斂。本文首先根據機械的轉速信息提取故障樣本的頻域信號，然后將其輸入到批標準化的深度神經網絡中進行訓練，最后采用Softmax回歸作為分類器實現轉速大波動下的智能故障診斷。隨即以兩種特殊設計的轉速大波動軸承故障試驗為例驗證了提出方法的有效性。

1批標準化的深度神經網絡

選用疊加自動編碼器經逐層訓練構成深度神經網絡，Softmax回歸判別結構作為分類層，將批標準化技術應用到網絡的每一激活層中，建立具有診斷監測能力的深度神經網絡模型。

1.1疊加自動編碼器

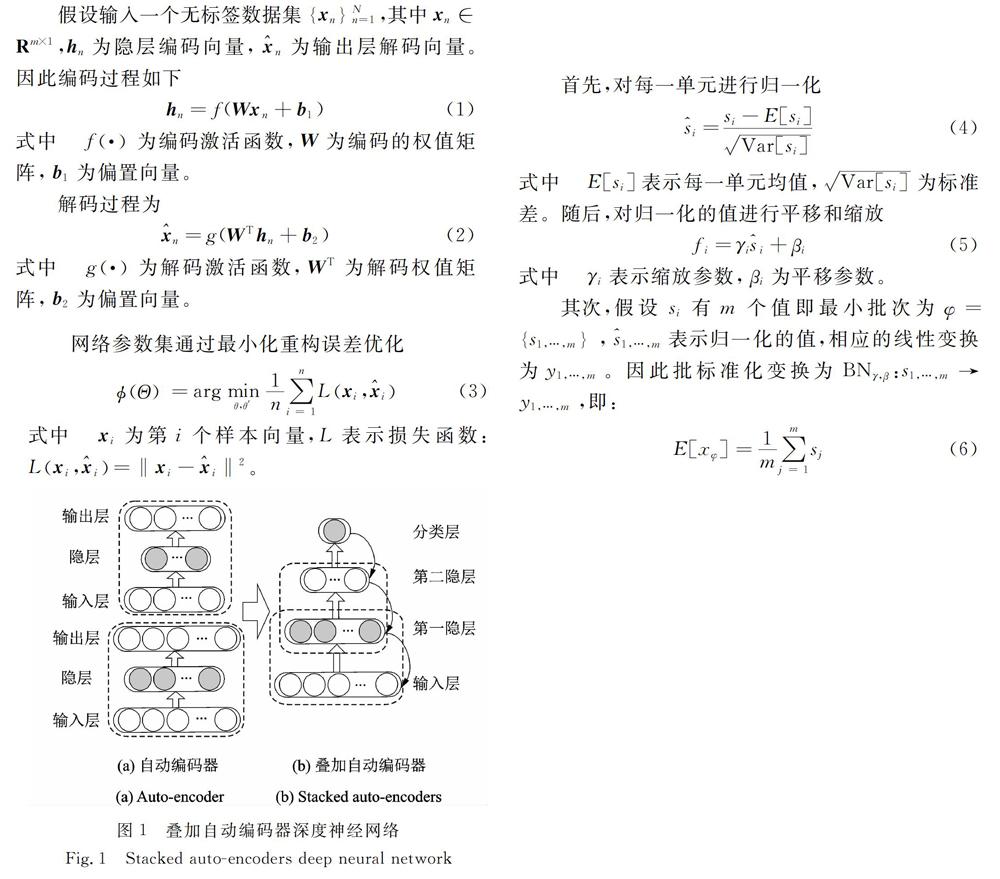
疊加自動編碼器的基本組成單元為自動編碼器結構。一個自動編碼器為對稱的三層神經網絡：輸入層、隱藏層和輸出層，結構如圖1（a）所示。其學習過程為非監督學習方式，包含編碼和解碼過程：編碼用于將輸人信號映射成隱層表達，解碼是對隱層表達的重構。

將自動編碼器逐層疊加，即第一隱層為第二層輸入，由此構成深度網絡結構，如圖1（b）所示。構成的深度神經網絡采用非監督學習方式實現逐層訓練，Softmax回歸分類器與標簽數據相結合，經BP算法實現網絡權值更新和參數微調。

1.2批標準化

批標準化可以用一種優雅的方式重參數化幾乎所有的深度神經網絡，其過程可以應用于每一個激活層而無需參數調節。它可以通過一個獨立的方式來標準化矩陣的每一行使其具有零均值和單位方差。假設一個k維輸人向量s=（s1…sk），為提升訓練及減少內協變量轉移問題，批標準化技術采用兩個必要的簡化步驟：

3試驗驗證

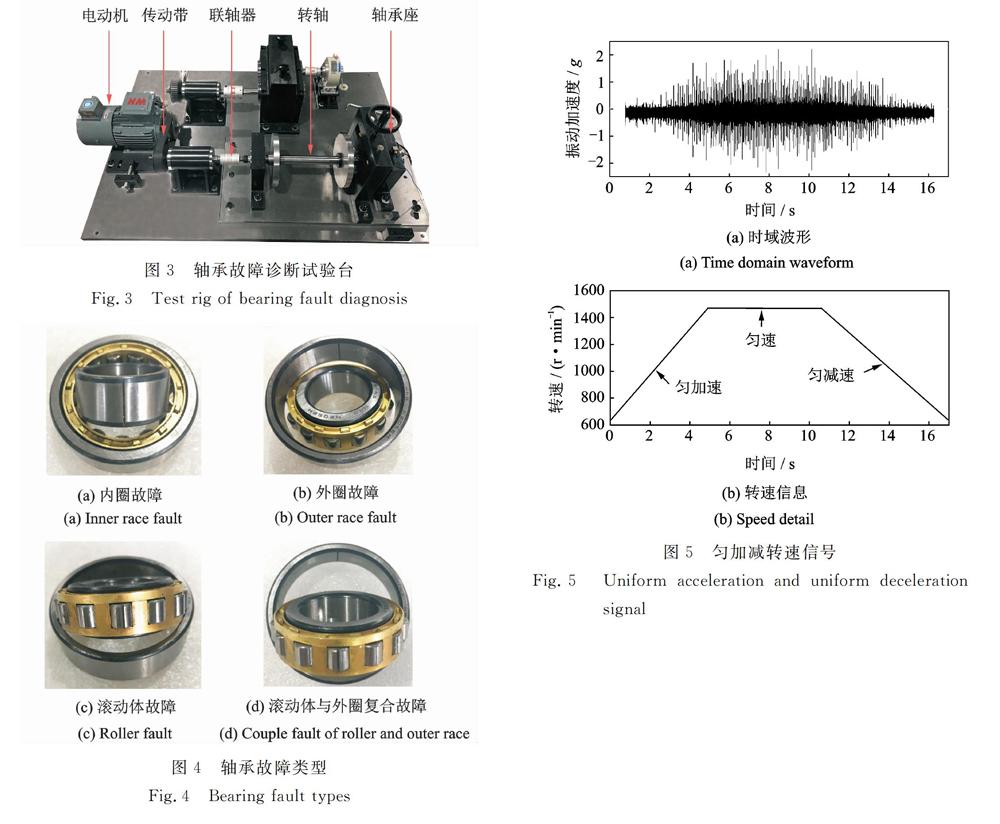
本文以軸承為研究對象，根據提出方法，采用兩種特殊設計的軸承轉速大波動試驗來驗證提出方法的有效性。軸承故障診斷試驗臺如圖3所示，驅動電機額定功率為0.75kW，軸承型號為QPZZ-II型NU205EM圓柱滾子軸承。故障設置為在軸承表面用線切割技術切出的方形凹槽，凹槽寬0.5mm、深0.5mm。共模擬設置了軸承的5種健康狀況：正常、內圈故障、外圈故障、滾動體故障、滾動體與外圈復合故障。故障軸承如圖4所示，在軸承座上表面安裝振動加速度傳感器，設置采樣頻率為25.6kHz。

3.1勻加減轉速大波動軸承試驗

設置軸承轉速從640r/min勻加速升到1500r/min，再從1500r/min勻減速到640r/min。以內圈故障軸承為例，時域波形如圖5（a）所示，經LMS數據采集設備提取轉速信息如圖5（b）所示。根據最低轉速及采樣頻率，取每個樣本2400個數據點，經FFT變換得1200個傅里葉系數。每種故障類型取200個樣本，共1000個樣本。之所以選用頻譜是由于時域樣本有時移特性，即在同一故障的不同樣本中，故障特征點的位置很難保證一致，由此給特征提取帶來較大困難;其次在深度神經網絡中，輸入分類器的每一個信號的長度都會影響準確率。因此為了包含足夠的信息并獲得較好的結果，就需要信號尺寸足夠大，然而過大的尺寸必然會導致網絡結構的復雜化及訓練時問加長。而頻譜信息不僅可以從測試信號中通過FFT輕松獲取軸承健康狀況更豐富的信息，而且更加規則化的特征分布克服了時域信號的時移特性;同時頻譜長度比時域信號尺寸縮短一半，減少了網絡的計算成本。

參照文獻[11]，本文網絡結構設置共5層，每層神經元個數分別為1200，600，200，100和5。試驗中隨機選取40%的樣本進行訓練，其余樣本用于測試。為減少隨機因素的影響，試驗重復進行15次。每層迭代次數為20次，學習率為10^-4，批尺寸為10。

診斷結果如圖6所示，可以看出15次試驗的訓練準確率均為100%，平均測試準確率為98.8%。因此足以說明提出的方法能夠排除轉速大波動的干擾，準確識別軸承的5種不同的健康狀況。為了對比提出方法的準確性，采用如下3種方法進行對比：

（1）對比方法1：采用時域信號作為輸入，網絡結構為2400-1200-600-200-100-5，其余參數設置與提出方法相同;

（2）對比方法2：未加批標準化算法的深度神經網絡，參數設置與文獻[12]相同。

（3）對比方法3：多隱層反向傳播神經網絡BPNN，結構與本方法相同。

同樣進行15次試驗，得到平均訓練和測試準確率如表1所示。可以看出提出方法在測試準確率上都遠遠高于其他方法，對比方法1的訓練準確率雖同樣達到了100%，但其測試準確率只有27.13%，這充分說明了時域信號的頻移和幅度特性對測試樣本產生的不利影響，雖然訓練準確率很高，但是在測試魯棒性上遠遠低于頻域信號。對比方法2和3無論在訓練還是測試準確率上都低于本方法，由此體現出批標準化算法在處理頻移和幅變特性數據上的優越性。圖7為3種方法的訓練誤差曲線，通過對比可以發現，提出方法不僅能夠在20次迭代步數中更快地收斂到0，而且在迭代初始階段便在一個很低的訓練誤差0.2下進行。對比方法1的初始訓練誤差為0.39，對比方法2和3無論在初始誤差及第20步誤差上均無法與提出方法相媲美。

為驗證提出方法的特征提取能力，利用t-SNE[20]技術將學習到的高維特征映射成三維特征向量進行可視化，結果如圖8（a）所示。可以看出除兩個復合故障的樣本與內圈故障混合，一個內圈故障樣本與滾珠故障混合外，其余不同類型的軸承樣本都很好地區分出來，相同類型的樣本都聚集在了一起。圖8（b），（c）所示為對比方法1和2的降維結果（方法3效果太差，在此不予展示），可以看出不同健康狀況的軸承樣本散點互相交錯，完全沒有呈現出聚集模式，說明這兩種方法相比于提出方法對勻加減轉速大波動下的故障特征提取能力上明顯不足。

為進一步說明批標準化技術中yi和βi參數的作用，隨機選取了3個不同轉速（700，1000，1300r/min）下的內圈故障樣本進行說明，如圖9所示。從圖9（d），（e）可以看出3種轉速下樣本的低頻部分發生頻移和幅變現象明顯，高頻部分幅變現象明顯。將其輸入到批標準化的神經網絡中后，得到各層的特征變化如圖10所示，可以看出隨著層數的增加，網絡學習到的特征逐漸趨向統一。圖11為未加批標準化得到的第三隱層特征向量圖，可以看出3個特征向量趨勢混亂，無法用于樣本分類。由此可以得出批標準化技術通過yi和βi逐層對樣本特征進行平移和縮放，使得最終提取的特征歸于同一趨勢，以此解決了轉速大波動下信號的頻移及幅變特性帶來的診斷困難問題。

3.2無規律轉速大波動軸承試驗

設置軸承轉速在800r/min到1500r/min之問無規律波動，同樣以內圈故障軸承為例，其轉速信息如圖12所示，持續采樣時問為32s。每種故障類型取360個樣本，總共1800個樣本。建立的深度神經網絡結構及參數設置不變。

采用10%的樣本進行訓練，其余樣本進行測試，得到15次訓練及測試準確率如圖13所示。可以看出提出方法在更少的訓練樣本百分比的情況下獲得了99.88%的平均測試準確率，比勻加減轉速大波動試驗的測試準確率更高。考慮其原因可能是由于該試驗的轉速波動較多，同等轉速信號樣本會多次重復采集，且轉速變化范圍較小。由此使得測試相對難度較小，且神經網絡結構維度也較小，網絡訓練起來相對容易，因此獲得準確率更高。同時根據如圖14所示訓練誤差及圖15所示特征降維散點圖可以看出，提出方法在處理無規律轉速大波動下的軸承故障診斷上同樣具有快速收斂和準確分類的優越性能。

3.3交叉驗證試驗

為進一步驗證提出方法的有效性，對上述兩節試驗進行兩組交叉驗證，具體如下：

（1）驗證試驗1：以勻加減速波動試驗數據為訓練數據，以無規律轉速波動試驗數據為測試數據進行試驗;

（2）驗證試驗2：以無規律轉速波動試驗數據為訓練數據，以勻加減速波動試驗數據為測試數據進行試驗。

同樣進行15次試驗，訓練準確率在上述兩節中均已展示，現得到測試準確率如圖16所示。兩組驗證試驗的平均準確率分別為99.91%和98.02%，可以看出以勻加減速波動試驗數據為訓練數據，以無規律轉速波動試驗數據為測試數據得到的準確率更高。究其原因應為驗證試驗2中信號的轉速波動范圍較小，即缺少600-800r/min的訓練數據，因此在應對驗證試驗1的低轉速樣本時準確率自然降低。由于訓練過程與上兩節試驗一致，故訓練誤差曲線也無差別，在此不予展示。

兩種驗證試驗的特征降維散點圖如圖17，18所示，驗證試驗1的所有故障類型都完美地區分開來，驗證試驗2中復合故障與滾珠故障有輕微重疊現象，且有兩個復合故障樣本錯誤分人了內圈故障中，這也與其得到的相對較低的準確率相匹配。因此，通過驗證對比可以得出，提出方法在交叉驗證試驗中仍然能獲得較高的準確率，實現了故障類型的正確分類和識別。

4結論

（1）提出的批標準化深度神經網絡方法能夠克服機械轉速大波動的干擾，實現不同健康狀況軸承的準確診斷。兩組特殊設計的轉速大波動軸承試驗完美地驗證了提出方法的有效性。

（2）頻域信號不僅能克服時域信號的頻移和幅度問題，且數據量比時域信號減少一半，在提供更有效信息的同時減少網絡計算成本。試驗結果也表明頻域信號能夠獲得比時域信號更高的測試診斷準確率。

（3）批標準化技術在克服轉速大波動下振動信號的頻移和幅變問題的同時，還能加快網絡收斂。對比未加批標準化的深度神經網絡，結果顯示批標準化的深度神經網絡能夠更加快速準確地實現轉速大波動下的軸承故障診斷。