基于勢博弈的擁堵收費雙層定價模型

劉鵬煌 （上海大學 管理學院，上海200444）

LIU Penghuang (School of Management, Shanghai University, Shanghai 200444, China)

0 引 言

隨著城鎮化進程不斷加快和汽車工業快速發展，我國許多城市面臨嚴重的交通擁堵問題，緩解交通擁堵刻不容緩。交通擁堵的原因主要有道路基礎設施不足，私家車數量急劇增加和出行者出行決策低效。道路基礎設施不足和私家車數量急劇增加都是剛性約束，在未來一段時間內還難以徹底改變，而出行者出行決策低效更易于改變。出行者出行決策低效主要體現在：出行者在選擇出行路徑時，相互爭奪出行成本較低的路徑，忽略自身決策對路網環境的影響；此外，出行者在選擇出行方式時放棄容量大的公交車而選擇更舒適的私家車，出行者低效的出行決策降低路網資源利用率，如果能夠通過某種方式改變出行者低效出行決策，提高路網資源利用率，就能有效緩解城市交通擁堵。

道路擁堵收費在提高出行者出行效率，緩解城市交通擁堵上卓有成效，目前已在倫敦、新加坡、斯德哥爾摩等城市成功實施，其本質是一種交通需求管理的經濟手段，目的是利用價格機制限制繁忙時段和繁忙路段上的車流密度，提高路網資源利用率。擁堵收費的難點在于擁堵收費定價，目前構建擁堵收費定價的方法主要有邊際定價法、瓶頸模型法和雙層規劃法。關于邊際定價法，Walter[1]首次定量研究道路擁擠的外部效應，提出短期邊際成本定價模型，確定傳統擁擠定價理論；Dafermos[2-3]將邊際成本定價理論應用于確定路網中不同等級用戶的收費模式，并將路段收費和路徑收費的問題公式化。關于瓶頸模型法，Vickrey[4]應用確定性排隊理論提出道路擁堵收費單通道瓶頸模型，該模型論述排隊擁擠的消漲過程和用戶的時間決策，用動態過程分析道路擁堵狀況，給出基于時間的擁堵收費定價方案；Henderson[5]在道路瓶頸模型中考慮計劃時間延誤和出行者出發時間決策，給出從道路流量出發的動態擁堵收費定價方法；吳子嘯和吳海軍[6]對Vickrey 提出的瓶頸模型進行改進，將出行需求由固定值改為彈性需求，將出行者特征由相同改為有差異，得到一個新的擁堵收費定價模型；盧曉珊等[7]基于瓶頸理論構建出行成本均衡的分層擁堵收費定價模型，討論不同機制下地鐵票價和停車收費策略。關于雙層規劃法，Yang 和Lam[8]認為雙層規劃模型是最佳的擁堵收費定價模型，并利用雙層規劃法對道路擁堵收費進行研究；Yang 和Bell[9]將次優分析的思想應用于雙層規劃，提出基于雙層規劃的次優收費方法，并采用基于靈敏度分析的算法進行求解；李志純等[11]建立彈性需求下以用戶盈余最大化為上層目標的道路擁堵雙層規劃模型，下層模型為彈性需求下的隨機用戶平衡，并利用懲罰函數法和步長加速法相結合的算法框架求解；姚紅云等[12]考慮異質出行者的影響，以時間價值不同對用戶特性進行分類，得到彈性需求下多類型用戶的擁堵收費模型。從現有的擁堵收費定價模型來看，邊際定價法未考慮時間、空間和交通量的變化，即路網在任意時間均處于穩定狀態，交通需求和出行成本不隨時間變化而變化；瓶頸模型法太過理想化，它把道路瓶頸的容量描述為一個連續的出行時間函數，并且是部分線性的，甚至將排隊過程納入靜態問題的范疇；雙層規劃法最貼近實際情況，它同時優化交通管理者與出行者的決策，但雙層規劃模型太復雜，不易求解。本文擬采用雙層規劃法構建擁堵收費定價模型，由于雙層規劃不易求解，考慮運用勢博弈將雙層規劃轉化成單層規劃，在保證擁堵收費定價模型貼近實際情況的同時，降低雙層規劃求解難度。

擁堵收費能否順利實施依賴公眾對該策略的支持，雖然擁堵收費能夠有效緩解城市交通擁堵，但該策略由于其收入的不透明和不公平仍然沒有被公眾所接受，為了克服該缺陷，提高公眾對該策略的支持程度，很多學者對擁堵收費及其返還政策進行研究。Goodwin[13]提出將道路擁堵收入三等分，分別分給政府、快軌和城市道路基礎設施建設及公交系統；Mireabel 和Rrymond[14]提出將擁堵收費收入重新分配給地鐵系統，并得到使擁堵收費政策更有效率的地鐵票價；姜沂兵等[15]應用累積前景理論分析用戶出行行為，建立擁堵收費及其返還的優化模型，得到不同需求分布下的最優收費和最優票價折扣費率。針對擁堵收費的不公平性問題，本文擬將擁堵收費與公交系統聯系起來，考慮將擁堵收費收入以公交票價打折的形式補貼出行者，如此既可以提高公眾對擁堵收費的支持程度，又能鼓勵出行者選擇公交車出行。

1 符號說明與模型假設

本文研究的路網由節點、路段和路徑組成，分別對應網絡圖中的點、邊和鏈。路網的決策者有出行者和交通管理者，首先考慮出行者與交通管理者的決策。出行者根據交通管理者給出的路段擁堵收費和路網補貼率選擇出行成本最低的路徑出行；反過來，交通管理者根據路段的出行者數量決定路段擁堵收費和路網補貼率，目標是最小化路網總出行成本。出行者與交通管理者的決策相互影響構成一個雙層規劃模型。其次考慮出行者之間的決策，出行者根據其他出行者的決策選擇出行路徑，只要出行者發現路網中有更低出行成本的路徑，就會改變自身的策略，而出行者的策略變化又會影響其他出行者的決策，出行者之間的決策相互影響構成一個非合作博弈。綜上，本文研究的問題可描述為一個雙層規劃模型，上層為交通管理者的決策模型，其目標是最小化路網的總出行成本，下層為出行者非合作博弈模型，每個博弈方最小化自身的出行成本。

1.1 符號說明

A為路網中路段的集合，A=｛1,2 ,…,a｝；R為路網中路徑的集合，R= ｛1,2 ,…,r｝；W為路網中OD對的集合，W= ｛1,2 ,…,w｝；M為路網中出行者類型的集合，M= ｛1,2 ,…,m｝；Rw為OD對w間的路徑的集合；Bm為第m類出行者對私家車的偏好程度；Va為路段a的出行者數量；對w間第m類出行者的數量；τa為路段a的擁堵收費；γ 為擁堵收費上限；θa為路段a的道路容量；為路段a上的自由流出行時間；β 為出行時間與出行量的相關系數，β 為常數，且β∈［0,1 ］；ta為路段a的出行時間；λ 為出行者單位出行時間的成本，且λ∈［0,+ ∞ ］；為0-1 變量，當路徑r通過路段a時為1，否則為0；μ 為公交補貼率，即公交票價減免的比例；εa為路段a的公交票價；為第m類出行者選擇路徑r的出行者數量；Pm為第m類出行者的策略，為非合作博弈的策略集，為第m類出行者選擇私家車出行時路段a的出行成本；為第m類出行者選擇公交車出行時路段a的出行成本為第m類出行者選擇路徑r的廣義出行成本；Um為第m類出行者的總出行成本；U為路網的總出行成本。

1.2 模型假設

假設1 假設出行者的出行方式只有公交車和私家車兩種，且出行者沒有固定的出行方式，具體選擇哪一種出行方式取決于出行者對公交車和私家車的偏好程度，出行者對哪種出行方式的偏好程度越大，選擇該出行方式出行的機率就越大。

假設2 假設路網中出行者不同時間的出行決策是在同一時間進行的，若以天為時間單位，則路徑的出行量等于當天選擇該路徑的出行者數量。

假設3 假設路網中的出行者均為日常上下班通勤的出行者，故認為出行者有自己固定的交通起止點，即OD對。假設4 假設路段的出行時間與出行量正線性相關，路段a的出行時間為其中Va為路段a的出行量為路段a的自由流出行時間，即車輛在不擁堵情況下正常駕駛消耗的時間，假設路網中所有出行者的單位出行時間成本相同。假設6 假設同種類型的出行者出行策略相同，即選擇各路徑的概率相等。

假設7 假設出行者是完全信息和完全理性的，即出行者能夠準確獲取路網上的信息，包括路段的出行時間、擁堵收費和路網的公交補貼率，且出行者總是選擇出行成本最低的路徑。

假設8 假設交通管理者只對私家車出行者收取擁堵收費，并以票價打折的形式補貼公交車出行者，交通管理者收取擁堵收費主要根據道路的剩余容量，不妨設路段a的擁堵收費。

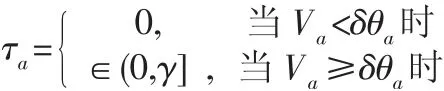
其中：θa為路段a的道路容量，γ 為擁堵收費的上限，δ 為比例系數，即一定比例的道路容量，δ 為常數，且

2 模型建立與分析

2.1 出行成本函數

本節擬構建第m類出行者的總出行成本函數和路網總出行成本函數。

引理1 路網中第m類出行者的總出行成本為：

路網的總出行成本為：

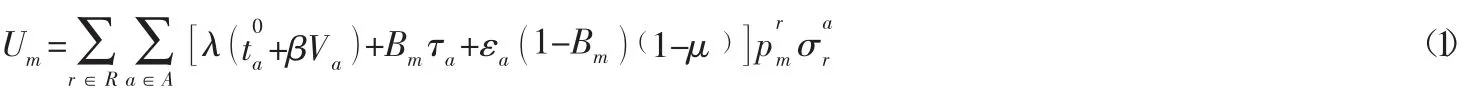
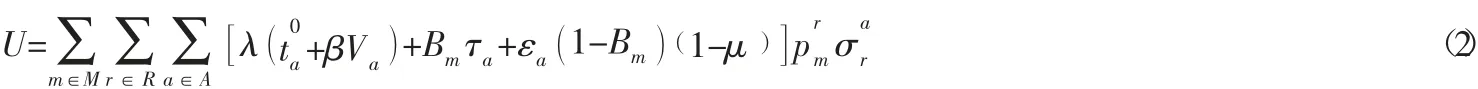
證明：按照出行者對公交車和私家車的偏好程度對出行者劃分，用表示第m類出行者對私家車的偏好程度，則1-Bm表示第m類出行者對公交車的偏好程度。又 表示第m類出行者選擇路徑r的數量，根據假設2 可得路徑r的出行量為：

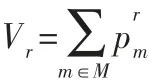
而路段出行量為通過該路段所有路徑的出行量的總和，故路段a的出行量為：

當出行者選擇私家車出行時，出行成本由時間成本和擁堵收費組成，根據假設4 可得第m類出行者選擇私家車出行時，路段a的出行成本為：

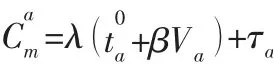
當出行者選擇公交車出行時，出行成本由時間成本和公交票價組成，其中公交票價為補貼后的公交票價，故第m類出行者選擇公交車出行時，路段a的出行成本為：

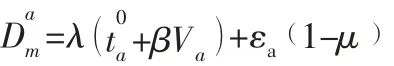
由假設1 可知出行者沒有固定的出行方式，因此用公交車出行成本和私家車出行成本的加權和表示出行者的廣義出行成本，路徑的廣義出行成本為該路徑所有路段廣義出行成本的總和，故第m類出行者選擇路徑r的廣義出行成本為：

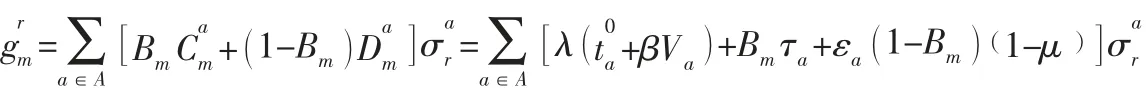
第m類出行者的總出行成本為所有路徑上第m類出行者出行成本的總和，故第m類出行者的總出行成本為：

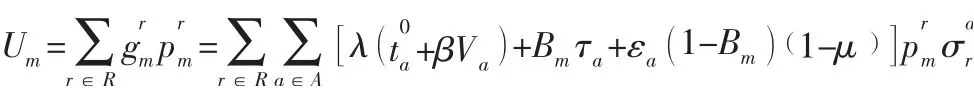
路網的總出行成本為所有類型出行者出行成本的總和，故路網的總出行成本為：

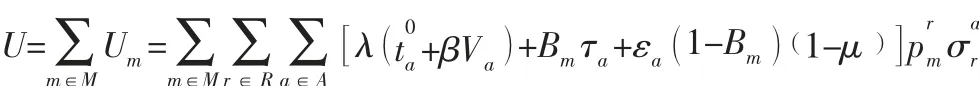
2.2 非合作博弈模型

本節擬構建出行者非合作博弈模型，由假設6 可知同類型的出行者選擇各路徑出行的概率相等，因此將路網中同類型的出行者視為一個博弈方，故路網中有多少種類型的出行者就對應多少個博弈方，博弈方m的策略為非合作博弈的策略集為P=P1×P2×…×Pm，博弈方m的支付函數為第m類出行者的總出行成本，則非合作博弈模型可描述為G

引理2 博弈G是一個精確勢博弈，且勢函數為：

證明：將式（3） 代入式（1） 得：

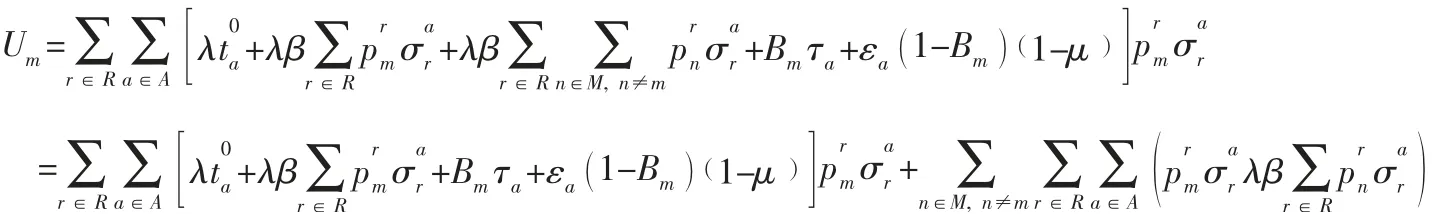
令：

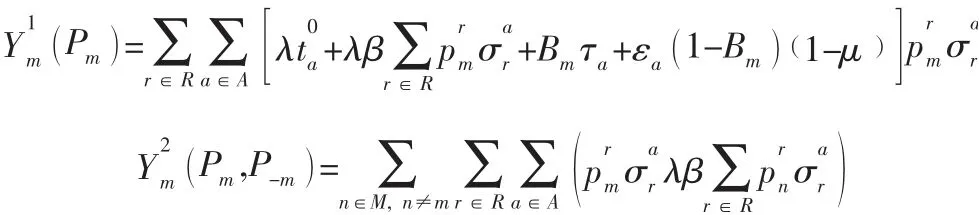
則：

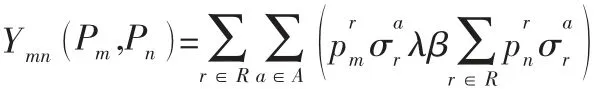
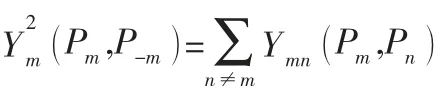
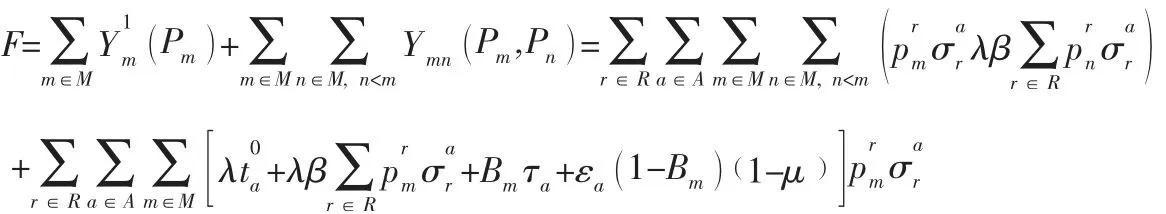
引理1 證明博弈G為精確勢博弈，根據精確勢博弈的性質，博弈G至少存在一個純策略Nash均衡，博弈G的Nash均衡策略滿足：

其中：P-m為除博弈方m外的博弈方策略，為博弈方m改變策略后的策略。

2.3 雙層規劃模型

在制定路段擁堵收費和公交補貼率時，交通管理者的目的最小化路網的總出行成本，當交通管理者給出每條路段的擁堵收費和公交補貼率后，各類出行者之間進行非合作博弈，各類出行者不斷調整自身的策略，最終得到Nash均衡，交通管理者根據Nash均衡策略調整路段擁堵收費和公交補貼率，直到非合作博弈Nash均衡條件下，路網的總出行成本最低，故可將式（4）作為交通管理者決策模型的約束，得到雙層規劃模型：

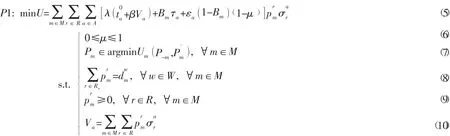
其中：式（5） 為交通管理者的目標函數，即最小化路網的總出行成本；式（6） 為公交補貼率的取值范圍；式（7） 為博弈G的Nash均衡條件；式（8） 為出行者的出行需求約束，即第m類出行者分配到OD對w間的出行者總數應等于第m類出行者在OD對w之間的總出行需求；式（9） 為第m類出行者選擇路徑r出行數量的取值范圍；式（10） 為路段a上的出行者數量。

2.4 雙層規劃模型轉換

由式（7） 可知，下層博弈G為多目標規劃，即所有博弈方的支付函數最小，這樣的特征使得P1 非常復雜，用現有方法很難直接求解。本文擬利用Nash均衡的定義，將博弈G轉換為若干個約束，利用這些約束限制博弈G的策略空間，進而將P1轉換為單層規劃。

對于每一個博弈方，其單方面的策略改變稱為策略偏差，本文用r維的向量表示博弈方m的策略偏差，其中為博弈方m在路徑r上的出行量變化。由于博弈方m的出行者總數不發生改變，即某條路徑上博弈方m的出行者數量增加，必有其它路徑上博弈方m的出行者數量減少，因而博弈方m的出行者數量變化滿足：

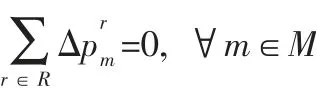
此外，路徑r上博弈方m的出行者數量變化滿足：

當博弈方m的策略從Pm變化為Pm+ΔPm時，支付函數的變化為：

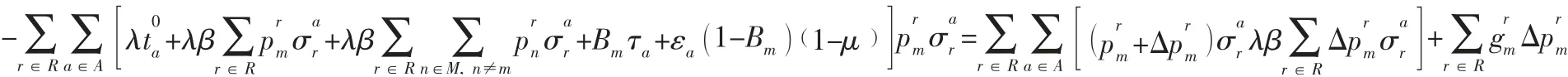
在Nash 均衡條件下，沒有哪個博弈方能夠通過策略偏差來降低自身的出行成本，因此出行成本變化滿足：

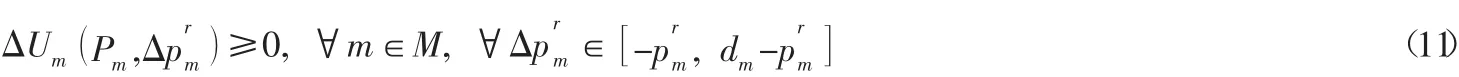
用式（11） 替換式（7） 得到下面的單層規劃模型：

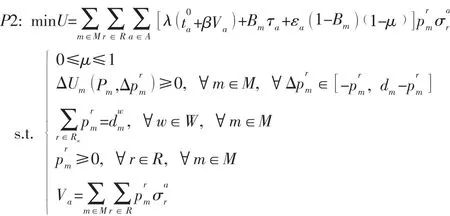
從式（11） 可以看出，變量的取值非常多，包括整數變量和連續變量，且整數變量的取值范圍非常大，處理比較困難，需要對式（11） 進一步簡化。本文考慮一種更簡單的策略變化，即簡單策略偏差，利用簡單策略偏差縮小整數變量的取值范圍。

簡單策略偏差是指博弈方只改變一對純策略的概率，其它純策略的概率保持不變。同樣用r維向量表示博弈方m的簡單策略偏差，博弈方m只改變純策略x和y的概率。令同理可得簡單策略偏差情況下，博弈方m的支付函數變化為：

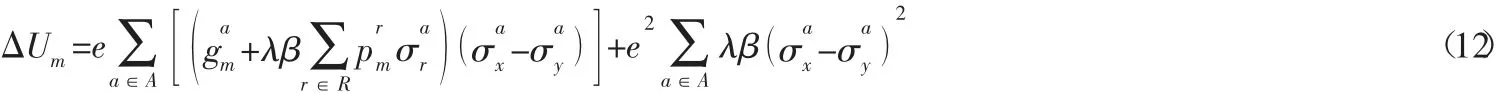
在Nash均衡條件下博弈方m的支付函數變化滿足由式（12） 可知ΔUm是關于e的一元二次函數，且開口向上，令ΔUm=0，可得：內成立，即滿足Nash均衡條件，必須要求e2＜0，故博弈G的Nash均衡條件為：

為保證

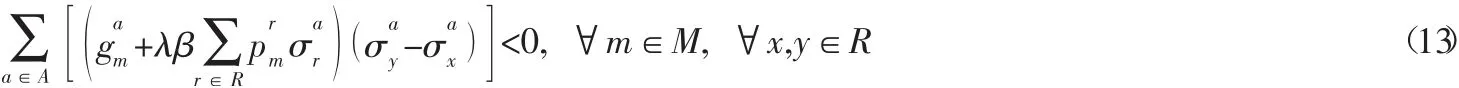
用式（13） 替換式（11），得到下面的單層規劃模型：

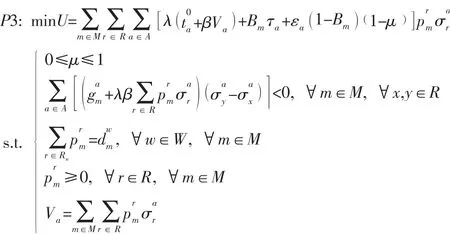
2.5 出行決策效率分析

Price of anarchy（POA） 是博弈論中的一個重要概念，字面意思是博弈方由于自私自利行為導致的效率損失，具體來講，它是度量博弈方分布式自私行為與Pareto最優的效率偏差，定義為博弈方非合作博弈的總支付函數值與合作博弈的總目標函數值之比。

在非合作博弈情形下，每一個博弈方最小化自身的支付函數：

在合作博弈情形下，每一個博弈方最小化博弈方的總支付函數：

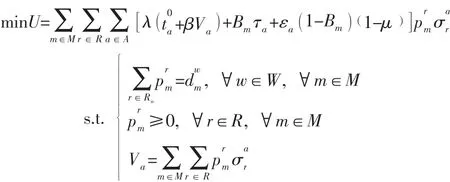
由式（14） 可知，對于交通管理者給出的τa和μ，POA的值越小，博弈方的總出行成本越接近Pareto最優，出行者的出行決策越高效，反之，出行者的出行決策越低效。

3 算例分析

通過一個具體的算例對單層規劃模型P3 進行分析，考慮如圖1所示的路網有4 個OD對：

路網中包含四種類型的出行者，各類出行者的數量均為230，各類出行者對私家車的偏好程度分別為：B1=0.2，B2=0.4，B3=0.6，B4=0.8。各OD對之間各類出行者的數量如表1 所示：

圖1 路網示意圖

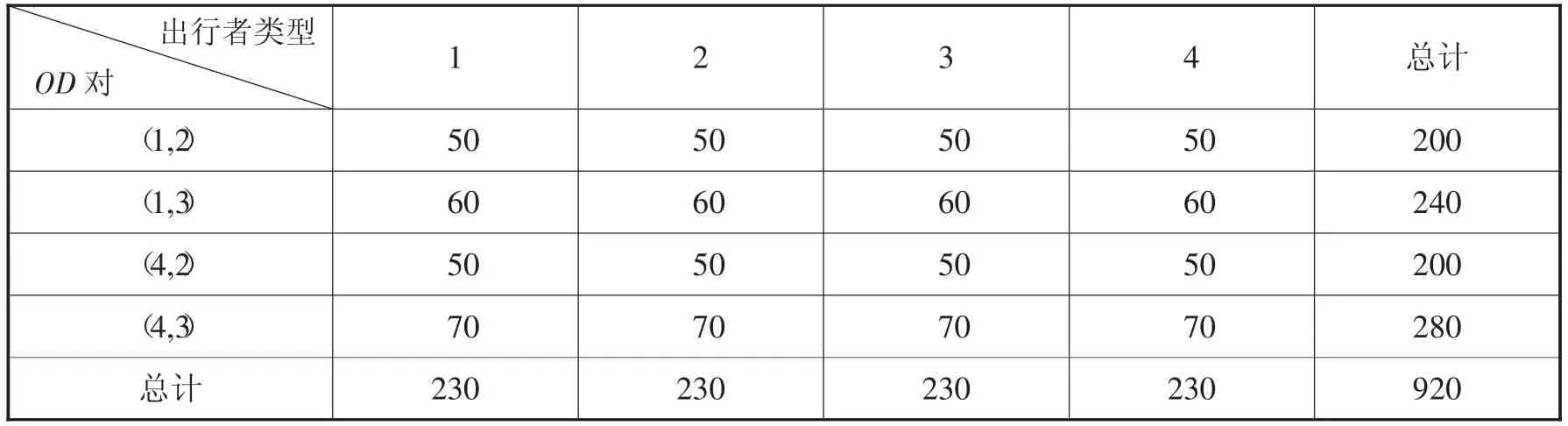
表1 OD 對之間各類出行者的數量

基于上述參數，通過Matlab7.0 軟件在無收費無補貼、有收費無補貼、有收費有補貼三種情形下，計算各類出行者的出行成本、路網的總出行成本和POA值。三種情形下各類出行者的出行成本如圖2 所示，橫坐標表示交通管理者的策略類型，縱坐標為各類出行者的出行成本。

從圖2 可以看出，從無收費無補貼，到有收費無補貼，再到有收費有補貼，各類出行者的出行成本逐次降低，這說明擁堵收費和公交補貼均能有效降低各類出行者的出行成本。比較出行成本的下降幅度可知，有收費有補貼的出行成本下降幅度最大，有收費無補貼次之，這說明擁堵收費和公交補貼同時實施的效果優于僅擁堵收費。

三種情形下，路網的總出行成本如圖3 所示，橫坐標表示交通管理者的策略類型，縱坐標表示合作與非合作兩種情形下路網的總出行成本。

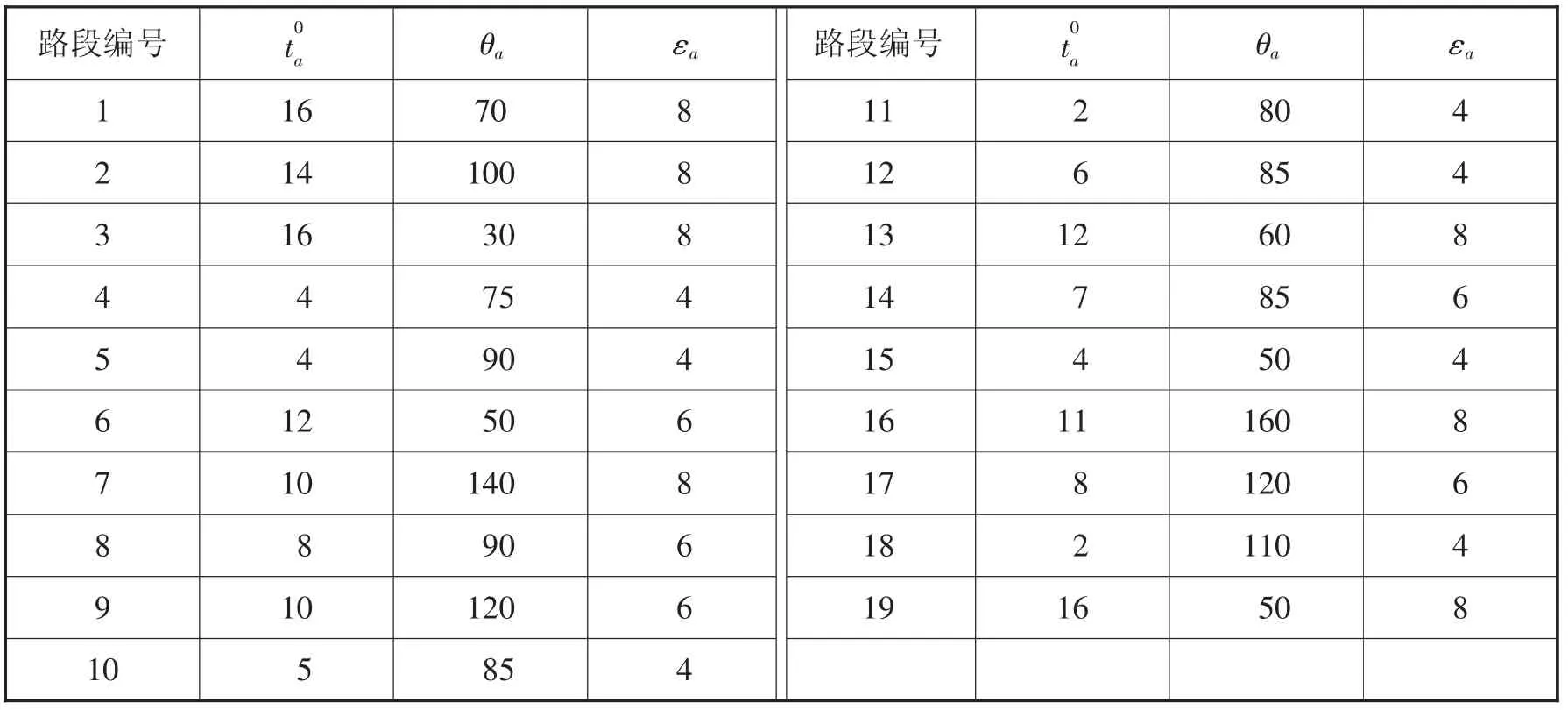
表2 路段參數

圖2 三種情形下各類出行者的出行成本

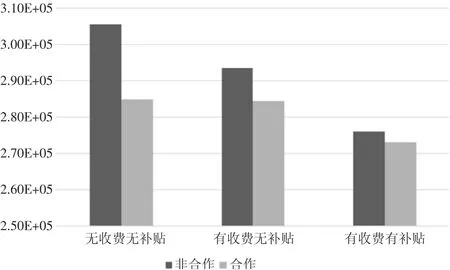
圖3 三種情形下路網的總出行成本

從圖3 可以看出，從無收費無補貼，到有收費無補貼，再到有收費有補貼，合作與非合作的路網總出行成本均逐次降低，這與圖2 得到的結果一致。比較出行者合作與非合作兩種情形下路網總出行成本可知，合作的路網總出行成本總是低于非合作的路網總出行成本。此外，有收費有補貼出行者合作與非合作的路網總出行成本差值最小，這說明擁堵收費和公交補貼均能減少出行者因利益博弈造成的損失，且擁堵收費和公交補貼同時實施時效果最佳。

三種情形下POA值如圖4 所示，橫坐標表示交通管理者的策略類型，縱坐標為相應的POA值。

從圖4 可以看出，三種情形下POA值均大于1，即非合作的路網總出行成本總是高于合作的路網總出行成本，這說明非合作得到的是低效率的Nash均衡，而合作博弈得到的是高效率的Pareto最優。比較三種情形下的POA值，從無收費無補貼，到有收費無補貼，再到有收費有補貼，POA的值逐次降低，這說明有收費有補貼時出行者的出行決策最高效，有收費無補貼其次，無收費無補貼最低。

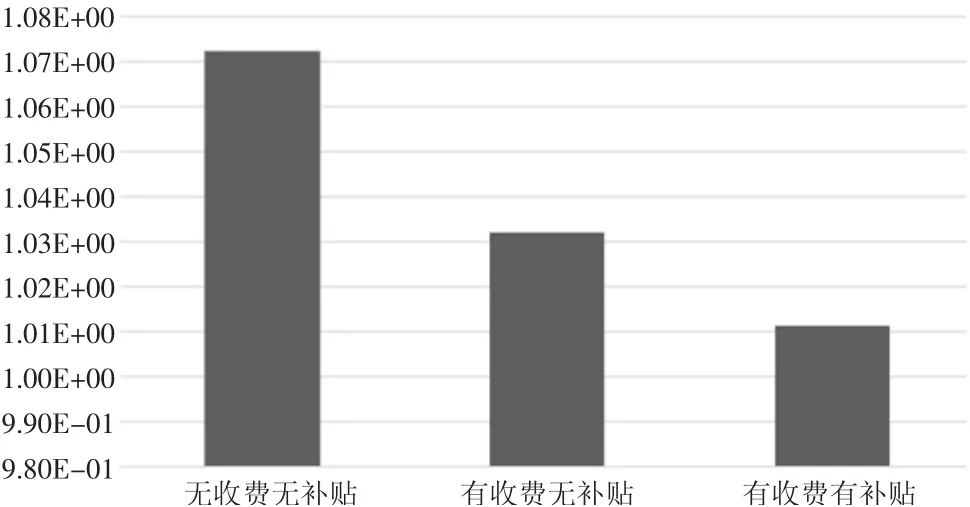
圖4 三種情形的POA 值

4 結 論

本文同時考慮擁堵收費和公交補貼，采用雙層規劃與博弈論結合的方法，構建擁堵收費定價模型，上層為交通管理者的決策模型，下層為出行者非合作博弈模型。利用勢博弈理論證明下層非合作博弈為勢博弈，從而下層非合作博弈存在Nash均衡。基于博弈方的策略偏差將雙層規劃模型轉換為易于處理的單層規劃。最后，通過具體的算例在不收費不補貼、有收費無補貼、有收費有補貼三種情形下，計算各類出行者的出行成本、路網總出行成本和POA值，結果表明：擁堵收費和公交補貼均能有效降低各類出行者的出行成本和路網總出行成本，使出行者的出行決策更高效，且擁堵收費和公交補貼同時實施的效果最優。