基于ARIMA模型的豆粕期貨價格預測方法研究及啟示

陳新華 劉潔

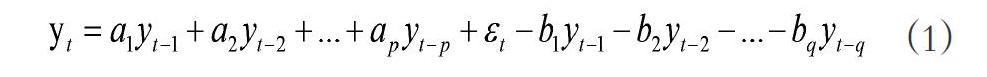
摘? ?要：受中美貿易摩擦持續升級和豬肉價格暴漲的影響，豆粕期貨價格的波動成為了當前社會各界關注的一個熱點問題。本文以2018 年1月2日至11月30日期間大連商品交易所豆粕期貨價格作為研究對象，分析了 ARIMA模型對于豆粕期貨價格預測的有效性。實證研究的結果顯示該模型在短期內對豆粕價格的預測精確度較高，但是隨著時間的推移其誤差開始增加。同時，通過ARIMA 模型所反映出來的豆粕價格相關性的滯后階數也可發現目前我國的豆粕期貨交易存在投機氛圍較濃等問題。基于以上分析，最后分別從投資者角度和期貨市場發展層面提出了相應的對策建議。

關鍵詞：豆粕期貨;ARIMA模型;價格預測

中圖分類號：F323.7 文獻標志碼：A 文章編號：1008-2697（2020）02-0023-04

一、引言

自2000年7月在大連商品交易所上市以來，豆粕期貨合約一直都是我國期貨市場中最為活躍、交易量最大的合約品種之一。豆粕期貨合約的標的物豆粕是菜籽粕、花生粕及棉籽粕等常見動植物油粕中產量最大的，其用途也極為廣泛，可用于畜禽的飼養、食品糕點及化妝品原料等等。豆粕價格的影響因素眾多，例如國際市場價格、季節性因素及國內外農業政策變化等等。豆粕價格的劇烈波動會給其產業鏈上下游企業的經營帶來風險，而價格發現和風險規避正是期貨市場的兩大主要功能;因此，我國的大豆生產商、加工商和畜禽養殖企業都可以利用豆粕期貨這種衍生品工具來規避豆粕現貨價格波動所帶來的風險。但是近年來，隨著中美貿易摩擦的升級和豬肉價格大幅上漲，造成豆粕現貨和期貨價格都出現了較大的波動，給相關的現貨經營者和期貨投資者都帶來了極大的風險。因此，本文試圖通過分析ARIMA模型對豆粕期貨價格預測的有效性，以期為我國豆粕期貨市場的參與者規避市場風險、保障豆粕產業持續化發展以及不斷提升我國期貨市場服務“三農”水平提供理論依據。

二、相關文獻評述

由于期貨市場采取的保證金制度，使得期貨交易相對于基礎金融產品而言存在較高的杠桿性，期貨交易高收益高風險的特點也使得對其價格的預測一直成為國內外學者研究的焦點問題。由于ARIMA 模型在研究金融時間序列上的一些獨有特點，使其成為了期貨合約價格預測的一種主流方法。上世紀70年代美國統計學家Boxgep與英國統計學家 Jenkins 最早開始利用ARIMA 模型進行了價格預測的研究。隨后我國的多位學者也開始嘗試利用ARIMA 模型

來預測期貨價格。如張珂（2016）選取了180個交易日的日度數據并利用ARIMA 模型對我國上海期貨交易所的銅期貨的價格進行了預測，對比2015年9月14日至9月25日十天的期貨合約的實際價格數據和預測數據后發現，在短期內ARIMA 模型可以較好的預測銅期貨的價格[1]。呂靖燁（2019）選擇了2013年到2018年EUA的期貨價格進行了模擬，通過對比各模型的AIC值和SC值，最終選擇了p=5，q=2的ARIMA 模型并得出了未來 3 個月碳期貨價格可能會有較大幅度的波動的預測結論[2]。除此之外，還有一些學者關注于研究如何提高ARIMA 模型預測的精確度，如陳林（2010）認為在利用ARIMA模型對期貨價格進行預測時，為了提高研究的精確度應該在p值和q值的確認上運用枚舉法來確定最優的預測組合[3]。國內外學者對于ARIMA 模型方法的運用已經較為成熟，而且研究的對象也在不斷豐富，如（費婧文，2017;魏蓉蓉，2011;高欣宇，2014;李戰江，2013）等，這些學者利用ARIMA 模型的研究對象已經從農產品期貨衍生到金屬期貨、能源期貨和金融期貨[4-7]。綜合已有的研究可以發現，大多數相關文獻都能根據預測的結果對投資者提出交易建議，但是并未過多的關注從期貨市場價格波動特點的角度對期貨市場的完善和發展提供建設性的意見。本文也將在這方面做一些有益的嘗試。

三、研究方法與數據來源

（一）研究方法

根據所要研究的金融時間序列的特點，ARIMA 模型可以分成三種形式，分別是：自回歸模型（AR）、移動平均模型（MA）和自回歸平均移動（ARIMA）。具體模型如式1所示：

其中其中：a1，a2，ap是自回歸系數;b1，b2，bp 是移動平均系數;εt是殘差。

具體建模過程主要可以分為以下幾個步驟：

第一，對所要研究的金融時間序列進行平穩性檢驗。如果序列平穩，則用ARMA模型直接對數列進行模擬;如果序列不平穩，則要進行差分后再做平穩性檢驗，最終來確定ARIMA模型中d的數值。

第二，通過自相關和偏相關圖初步判斷p和q的階數，再通過對比各模型AIC以及BIC等數值，選取最合適的ARIMA模型。

第三，運用確定的模型形式來計算模型中研究對象的滯后項系數。

（二）數據來源

本文選擇了大連商品交易所2018年1月2日到11月30日的豆粕期貨的收盤價作為研究對象。農產品期貨合約的交易具有向主力合約集中的特點，其他月份交割的期貨合約的交易量相對較少，例如2018年3月5日至14日，大連商品交易所的M1803連續出現了交易量為0的情況。為了保持價格的連續性，本文的期貨價格選擇盯住豆粕1月、5月及9月交割的三個主力合約的收盤價。具體做法是，從2018年1月2日開始盯住M1805的收盤價作為豆粕期貨的價格，但是在最后交割日的前一個月轉為盯住M1809的收盤價作為豆粕期貨的價格，以此類推。這么做的目的是可以選取流動性較好的三個主力合約的價格來代表豆粕期貨的價格，保持了期貨價格的連續性。同時，在最后交割月的前一個月轉換合約可以防止在臨近最后交易日時因投資者急于平倉而造成的期貨價格出現異常波動的情況。

豆粕期貨價格的數據特征如表1所示：

樣本的總數為233個，其中前213個用于確定豆粕期貨價格預測的ARIMA模型的形式，后20個用以驗證模型的準確性。

四、實證分析

（一）平穩性檢驗

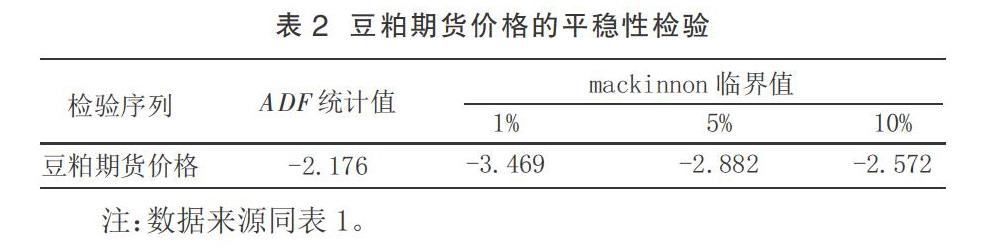
首先對豆粕期貨價格的時間序列進行平穩性檢驗，檢驗的結果如表2所示：

從表2的結果中可以看出，豆粕期貨價格平穩性檢驗的ADF統計值未能通過10%水平下的檢驗，在0.215的概率下不能拒絕原假設。進一步對豆粕期貨價格進行一階差分后做平穩性檢驗，結果如表3所示：

豆粕期貨價格一階差分后ADF統計值為-4.442，小于 1%、5%、10%三個顯著性水平下的臨界值 -3.471、-2.882和-2.572，說明豆粕期貨價格一階差分序列在 1%的顯著性水平下為平穩序列。因此可以選取一階差分后的時間序列作為建模序列并確定 ARIMA模型中的p 和 q 值。

（二）建立豆粕期貨價格的預測模型

根據平穩性檢驗結果，原期貨價格序列經過 1階差分后變平穩，所以取d=1。接下來再來確定 ARIMA（p，d，q）模型中 p 和 q 的階數。對于不同的p，q 取值，分別建立模型，并進行參數估計，比較各模型參數的 t統計量以及信息準則值（AIC 準則和 BIC準則），根據系數的顯著性以及 AIC 和BIC 最小化準則來判斷并選出最優模型。首先對豆粕期貨價格做自相關系數檢驗（ACF），結果如圖1所示：

豆粕期貨價格的滯后期對當前的價格產生了一定的影響，但是隨著滯后階數的增加，這種影響越來越弱，當落入灰色區域之后表明該滯后期對當期價格影響和0沒有顯著的區別。進一步對豆粕期貨價格做偏自相關系數（PACF）檢驗，結果如圖2所示：

通過圖2可以看出只有在滯后一階有一個顯著的偏自相關系數，其他各階都位于置信區間內。根據AC和PAC圖形可以初步判斷該時間序列存在AR過程，其中具體表現為：（1）AC 圖“拖尾”;（2）PAC 圖“截斷”，截斷處對應的階數就是AR的滯后階數P。因此，通過圖1和圖2可以大體判斷該時間序列存在一個AR1的過程。

為了進一步確定ARIMA模型形式，下面分別利用ARIMA（1，1，0）、ARIMA（1，1，1）、ARIMA（1，1，2）、ARIMA（2，1，0）、ARIMA（2，1，1）和ARIMA（2，1，2）6種形式分別對2018年1月2日到11月30日的豆粕期貨的收盤價數據進行模擬，然后對比各模型系數的顯著性。

對比各模型的模擬結果可以發現，所有模型中的常數項都不顯著，其中ARIMA（1，1，1）的系數的顯著性最好，其次是ARIMA（1，1，2）。進一步對比各模型的AIC和BIC值如表5所示：

從表5的對比結果可以發現，ARIMA（1，1，1）的AIC和BIC值最小，由此確定豆粕期貨價格預測

模型形式，并利用本文所選取2018 年 1 月 2 日至 11 月 30 日期間的后20個真實數據與預測數據進行對比，以檢驗預測模型的有效性。對比結果如圖3所示：

五、結論與啟示

本文以2018 年1月2日至11月30日期間大連商品交易所的期貨價格作為研究對象，分析了利用 ARIMA模型對豆粕期貨價格進行預測的可行性。通過對比6種模型的系數顯著性以及AIC和BIC的數值發現ARIMA（1，1，1）具有最好的模擬效果，根據豆粕期貨價格真實值與預測值對比也可發現該模型在短期內具有一定的精確度，預測值和真實值之間的誤差并不大;但是隨著時間的推移預測的精確度在不斷的衰減。出現這種情況的原因一方面源于ARIMA模型自身的特點，另一方面可能是由于目前投資者所面臨的復雜的供需預期環境。豆粕期貨價格的影響因素眾多，除了替代品的價格、季節性因素外還會受到國際價格及相關的農業、貿易、食品政策影響。當前中美貿易摩擦帶來的不確定性以及我國大豆的進口呈現出多元化的特點都可能導致我國的豆粕期貨的價格波動頻繁[8][9]。上文的研究結論也帶來了以下啟示：

第一，期貨投資者在當前復雜的市場環境下不應盲目的追漲殺跌。例如，2019年下半年以來不少投資者認為豬肉價格上漲將造成豆粕需求增加會促使豆粕期貨價格上漲，從而大資金的做多豆粕期貨合約。但是，實際的結果卻是豆粕期貨從高點3016元/噸，一路跌至2812元/噸方才企穩，使得不少多頭投資者虧損了近30%。為了減少風險，套期保值者應該根據實際規避風險頭寸來選擇合適的交易量和方向。投機交易者則應多考慮建立跨期、跨品種或者期貨加期權的組合來降低投資的風險。

第二，豆粕期貨價格所反映出來的ARIMA模型中的自相關階數為一階也表明了我們的豆粕期貨市場的投機氛圍較濃。投機者的介入可以大大提高期貨市場的流動性，保障了價格發現和套期保值兩大功能的實現。但是，期貨市場建立的初衷是為了提供給相關經營主體一個轉移價格風險的有效途徑。我國的期貨市場應當加大宣傳的力度，多鼓勵豆粕產業鏈條上的相關企業利用期貨市場來規避風險。同時應通過不斷增強我國期貨市場的風險控制能力、降低準入門檻和保值成本等方式，切實提升我國期貨市場服務于“三農”的能力。

參考文獻：

[1] 張珂.基于ARIMA模型的滬銅期貨價格預測研究[ J ].商，2016（07）：188-189.

[2] 呂靖燁.基于ARIMA模型的歐盟碳金融市場期貨價格預測及啟示[ J ].煤炭經濟研究，2019（10）：23-29.

[3] 陳林.基于ARIMA模型的期貨價格分析與預測[ J ].福州大學學報（哲學社會科學版），2010（05）：32-37.

[4] 費婧文.基于ARIMA模型對我國黃金期貨價格分析與預測[ J ].當代經濟，2017（03）：149-150.

[5] 魏蓉蓉.國際原油期貨價格波動趨勢分析——基于ARIMA模型的實證研究[ J ].價格理論與實踐，2011（11）：68-69.

[6] 高欣宇.對我國棉花期貨價格預測的方法研究——基于EGARCH-EWMA模型與ARIMA模型比較[ J ].價格理論與實踐，2014（12）：85-87.

[7] 李戰江.基于ARIMA模型的滬深300股指期貨價格預測研究[ J ].魯東大學學報（自然科學版），2013（01）：22-24.

[8] 黃亞林.我國農產品期權發展的制約因素分析[ J ].南方農村，2017（10）：41-44.

[9] 吳少戀.中加菜籽油期貨市場波動溢出實證研究[ J ].南方農村，2013（09）：14-18.

（責任編輯：羅湘龍）