基于LCD與峭度-能量比準則的滾動軸承故障診斷研究*

楊文志，張茹軍，安文斌

（內蒙古科技大學 機械工程學院，內蒙古 包頭 014010）

0 引 言

滾動軸承作為機械傳動部件中重要的組成成分，一旦發生故障將會對整個機械傳動系統造成巨大的影響，因此開展滾動軸承故障診斷的研究非常必要。

局部特征尺度分解是一種新的信號分解方法，近年來在非平穩、非線性信號的分解中得到廣泛應用，該方法具有以下優點：（1）提高了運算速度；（2）相對于EMD、LMD、ITD等方法，LCD的迭代次數更少，在抑制端點效應、模態混疊等方面更有優勢，具有更好的時頻局部化特性[1]。

文獻[2]提出了LCD與排列熵相結合的故障診斷方式；文獻[3]提出了LCD與基本尺度熵相結合的故障診斷方式；文獻[4]提出了將LCD與互近似熵相結合的故障診斷方式；許多學者采用了EMD、VMD等與各種熵或者能量相結合的方式，來診斷齒輪或滾動軸承的故障[5-7]。多特征值融合可以彌補單一特征的局限性，但是大量的特征值結合容易導致特征冗余，計算量大，會影響故障分類的結果。因此，峭度準則、相關系數法、特征加權等方式被應用于篩選有效分量。

本文將采用LCD對滾動軸承信號進行分解，根據峭度-能量比準則，計算各ISC分量的Kr值，選取Kr值較大的ISC分量作為有效分量，計算其能量熵和多尺度熵，以此作為特征向量。

1 理論介紹

1.1 LCD分解方法

LCD方法是將復雜的振動信號分解成具有不同能量并且相互獨立的ISC分量，分解時需要滿足以下條件：

（1）在尋找極值點過程中，使得所有相鄰兩個極值點保證符號互異；

（2）在構建基線信號前設定點（xk,τk）,其中：k=1,2,3,…,M；該點代表極值點以及對應的時刻，時刻點τk+1在左右相鄰兩個極值點構成的線段上相對應的函數值為Ak+1，函數值Ak+1與極小值xk+1的關系是比值近似不變。

函數值Ak+1的表達式如下式所示：

（1）

通過以上條件保證了分解形成的ISC分量符合正弦曲線特性，使得其在任意兩個相鄰極值點之間具有單一模態。

分解流程如圖1所示。

圖1 LCD分解流程圖

LCD分解的結束條件有標準偏差法、閾值法和極值單調性這3種，本文LCD分解結束采用的是極值單調性方式。

從美國Spectra Quest公司機械故障綜合模擬試驗臺采集滾動軸承內圈故障數據，進行LCD分解后獲得的波形圖如圖2所示。

圖2 LCD分解圖

1.2 峭度-能量比準則

信號經LCD分解為多個ISC分量，分解的ISC分量的頻率是由高頻到低頻產生的，其幅值和頻率都會有所衰減，能量逐漸降低，且容易在低頻區產生虛假分量。

能量比系數表達如下式所示：

（2）

式中：ε—能量比系數；EISC（i）—不同分量具有的能量；Ex—總能量。

分解形成的ISC能量比值是不同的，單純采用能量比準則提取有效分量存在一定誤差，因此，筆者將能量比與峭度值相結合來綜合分析。

將其定義為ISC分量的Kr值為：

Kr=αK+（1-α）ε

（3）

式中：K—ISC分量的峭度值；ε—不同ISC分量的能量比；α—不同的ISC分量的峭度值對Kr值的權值度。

計算各個ISC分量峭度、能量比和Kr值，如表1所示。

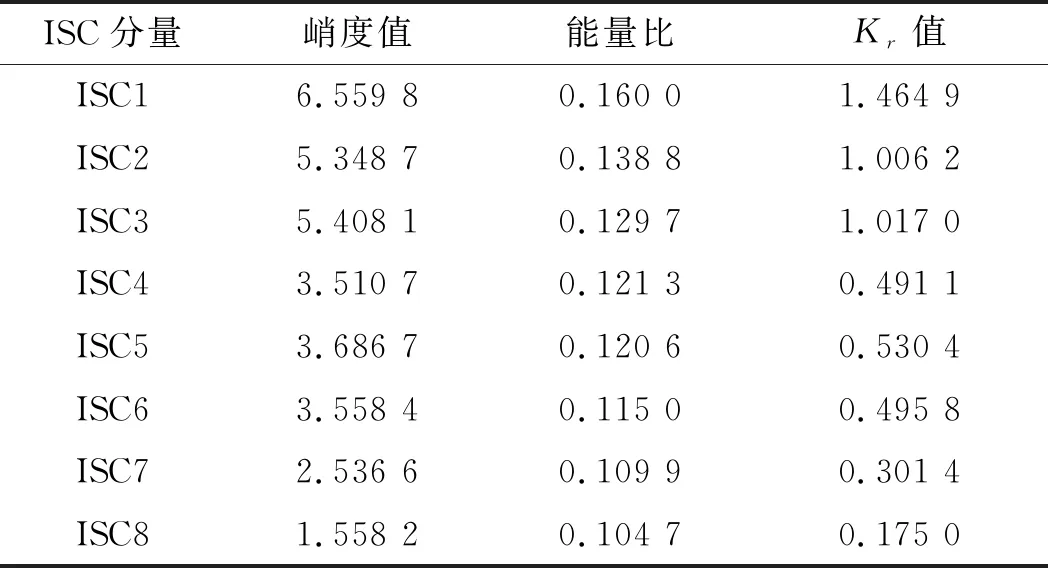
表1 各ISC分量峭度、能量比和Kr值

表1說明：ISC1分量具有的Kr值約為1.5，ISC2分量與ISC3分量的Kr值約1，而其他分量的Kr值≤0.5。

因此，筆者選用ISC1、ISC2與ISC3這3個分量的特征。

1.3 能量熵

LCD信號分解將原始故障信號分解成具有不同能量的分量，各分量的能量依次減少，殘余分量的能量很小，因此可以忽略不計。

能量熵定義如下式所示：

（4）

式中：E—不同分量上具有的幅值能量；Esum—信號的總能量；pi=Ei/Esum。

采用滾動軸承內圈故障信號進行LCD分解，分解后能量熵如表2所示。

表2 LCD能量熵

1.4 多尺度熵

多尺度熵是基于樣本熵的一種改進方法，用于描述時間序列在不同尺度熵的無規則程度[8]。它可全面反映信號的復雜度,能很好地區分不同故障,被廣泛應用到機械故障診斷領域[9-10]。

多尺度熵的計算步驟如下：

（1）進行粗粒化計算，以獲得新的時間序列：

（5）

式中：x（i）—原始序列；τ—尺度因子，當尺度τ=1時，即為原始時間序列。

（2）將新的時間序列然后組成一組矢量，其中：Y（τ）i=1,2,N-m+1；

（3）計算不同矢量下差值的絕對值最大值的距離d[Y（τ）（i）,Y（τ）（j）]，其表達式為：

d[Y（τ）（i）,Y（τ）（j）]=
maxk=0,…,m-1（|yτ（i+k）-yτ（i+k）|）

（6）

（5）多尺度熵定義：

（7）

式中：τ—尺度因子；m—嵌入維度；r—閾值。

多尺度熵中參數的變化將會影響最后的輸出結果，參數有尺度因子τ、嵌入維度m和閾值r。通常取r的值為0.1SD～0.5SD（SD是原始數據的標準差），尺度因子τ取值范圍為120。通過對比分析發現：當尺度因子τ取9時，滾動軸承各故障的樣本類間距離值為最大。

因此，此處選擇τ為9。

計算滾動軸承內圈故障下的多尺度熵，如圖3所示。

圖3 多尺度熵曲線

由于分解形成第1個模態具有的信息是最全面的，筆者選用第1個模態的多尺度熵。參考其他文獻，筆者設定m=2，τ=20。

圖3說明：r取值越小，MSE值整體越大，r取值越大，MSE值整體越小；但是當r的取值越小時，MSE曲線波動較為明顯。

因此，綜合考慮筆者取r=0.2。

選用滾動軸承內圈故障數據分解形成的ISC分量計算多尺度熵，如表3所示。

表3 ISC1的多尺度熵

1.5 SVM原理

支持向量機被廣泛應用于設備狀態監測和壽命預測等方面，其是在線性最優分類超平面的基礎上，在線性情況下，構造出一個最優超平面。它將需要解決的問題轉化為求取凸二次規劃問題中的最大間隔和最小化錯分程度，通過引入懲罰參數c來權衡兩者的比重。

支持向量機給設樣本集為（xi,yi），其中：n—數據個數，i=1,2,3,…,n；xi—類屬性，xi∈Rm；yi—類標記，yi∈（1,-1）。

支持向量機將低維空間的輸入映射到高維空間，尋找最優超平面。

超平面定義如下:

（8）

式中:ai—拉格朗日乘子;K（x,xi）—核函數;b—偏置。

本文選用高斯徑向核函數為:

（9）

2 滾動軸承故障診斷步驟

滾動軸承故障診斷的具體步驟如下：

（1）對采集到的振動數據進行LCD分解，獲得不同的ISC分量；

（2）對LCD分解產生的分量，運用峭度-能量比準則提取有效分量；

（3）計算有效ISC分量的能量熵，并對能量熵進行加權處理，獲得不同權值比重的能量熵；

（4）計算有效ISC分量的多尺度熵；

（5）進行融合構建特征向量，輸入支持向量機進行分類識別。

3 滾動軸承故障診斷實驗及分析

滾動軸承實驗數據來自美國Spectra Quest公司機械故障綜合模擬試驗臺。機械故障綜合模擬試驗臺如圖4所示。

圖4 機械故障綜合模擬試驗臺

筆者選用6205-2RS深溝球軸承作為測試軸承。測試軸承滾珠個數為9個，滾動體直徑為7.94 mm,軸承徑節為39.04 mm；實驗室電機轉速1 500 r/min，采樣頻率為33 kHz，采樣點數4 800。

參考文獻[11-13]中的樣本數目，在滾動軸承正常、內圈故障、外圈故障、滾動體故障這4種狀態下，分別采集60個樣本，共獲得240個樣本數據。在每種狀態下，隨機選擇30組數據作為訓練樣本，剩余的30組數據作為測試樣本。

上述滾動軸承振動信號經過LCD分解，共獲得8個ISC分量。運用峭度-能量比準則，篩選其中的3個有效分量，計算其能量熵與多尺度熵，然后輸入SVM中進行分類，最后得到結果。

根據上述診斷步驟，可得到滾動軸承故障診斷準確率如表4所示。

表4 故障診斷準確率

再將上述滾動軸承振動信號經過LCD分解，共獲得8個ISC分量，分別計算8個ISC分量的能量熵和多尺度熵，并輸入SVM進行分類，最終得到滾動軸承的故障診斷結果，如表5所示。

表5 故障診斷準確率

由表（4,5）數據可以說明：

（1）使用多特征進行故障診斷的準確率高于單一特征的準確率；

（2）篩選后的ISC有效分量提高了滾動軸承故障診斷的準確率。

4 結束語

采用LCD信號分解與峭度-能量比準則相結合的方法，本文進行了滾動軸承故障診斷：首先采用LCD對滾動軸承信號進行了分解，根據峭度-能量比準則，計算了各ISC分量的K_r值，然后選取K_r值較大的ISC分量作為有效分量，計算了其能量熵和多尺度熵，以此作為特征向量；該方法提高了故障診斷的準確率。得到結論如下：

（1）將能量熵、多尺度熵分別作為滾動軸承的故障特征，并對比兩者的故障診斷準確率，結果表明：內圈為6.6%，外圈為10%，滾動體為6.7%；

（2）運用峭度-能量比準則篩選ISC分量，能夠提高滾動軸承的故障診斷準確率；結果表明，滾動軸承內圈、外圈的故障診斷準確率分別提高了3.4%，3.3%。