考慮自適應行為的研發網絡風險傳播模型構建及仿真

楊乃定，王京北，張延祿，宋 悅

(1.西北工業大學管理學院，陜西 西安 710072；2.西北工業大學應急管理研究所，陜西 西安 710072)

1 引言

為了適應市場環境的變化，降低研發成本并分擔研發風險，研發網絡成為了研發項目運作的重要趨勢[1-2]。研發網絡指研發企業間為達到共同開發新產品或新技術、獲得互補的研發資源、縮短研發周期以及減少研發投入等戰略性目標，通過契約、合作協議或社會關系而形成的能夠自我學習的技術創新網絡[3]。研發網絡的運作形式可以為研發企業提供互補性的資源，降低企業的研發成本，提升網絡創新績效，但由于網絡結構的復雜性和外部環境的不確定性，使得研發網絡涌現出新的風險問題，比如技術風險和企業違約道德風險等。在研發網絡中，如果某家企業因為技術變革、自身經營不善等原因而破產或者直接退出網絡，與其進行技術合作的企業也會因此面臨較大的風險，進而也有可能會破產或者直接退出網絡，這種企業之間風險相繼傳播現象我們稱之為研發網絡風險傳播[4]。

已有關于研發網絡風險傳播問題的研究往往是從靜態網絡的視角出發，即認為在風險傳播過程中網絡的拓撲結構是不會自身主動發生改變的[5-9]，而很少從動態網絡的角度進行分析。動態網絡視角下的研發網絡風險傳播問題與靜態視角相比，最大的不同就是除了風險傳播導致的網絡結構變化外，網絡自身可以進行自適應性調整從而改變網絡結構[10]。比如對于網絡內研發企業A而言，如果與其合作的企業B面臨較大危機，從風險規避的視角出發為了避免自身利益受到損失，A可能會主動斷開與B的合作關系，這種情況下企業B面臨的危機只會對其他與其合作的企業產生影響，而不會對企業A造成損失。

研發網絡中風險傳播動力學會影響網絡的拓撲結構，而企業也會通過自適應行為改變網絡的拓撲結構從而對下一步的風險傳播產生影響，動力學過程與拓撲結構之間互相影響形成了反饋回路，這是自適應網絡的典型特征[10-13]。這其中蘊含著兩個重要的概念，即網絡動力學和網絡傳播動力學，前者重點考慮在固定的網絡中節點狀態的改變，以及在一個界限清楚的拓撲空間內系統狀態的變化軌跡，這是傳統動力學系統研究轉向狀態變量彼此交互的高維拓撲空間的自然延伸；后者強調的是網絡拓撲結構的轉變以及其對網絡統計特征的影響，其中一些重要的概念和技術都是從統計物理學和社會網絡分析中借鑒過來的。

Gross等[10]在2006年提出了自適應網絡傳播動力學的概念，打破了網絡自身結構的動態變化與網絡傳播動力學各自獨立研究的范式，結合現實生活背景中網絡拓撲結構的調整與網絡傳播動力學的交互影響進行了分析。Schwartz和Shaw[11]則針對自適應模式進行了系統的模型分析和評述，歸納出該理論的普遍性和有效性，并提出其在傳染病預測和控制方面的重要應用價值。Rattana等[12]針對自適應空間網絡進行了研究，對自適應行為施加了規則約束，即網絡中節點在進行重連的過程中只能選擇同一局域范圍內的節點進行連接。相關的研究已經證明自適應網絡是普遍存在的，尤其在以人為主導的社會網絡以及企業網絡中[13]。

在研發網絡中我們同樣可以看到，企業之間的狀態互相影響可能會導致風險傳播，同時企業之間的合作關系變動也導致網絡的結構發生變化，在具有自適應特征的研發網絡中企業狀態的變化和網絡結構的變化相互耦合，會導致更為復雜的網絡行為。鑒于現實情況下研發網絡風險傳播與自適應行為的典型特征，在考慮自適應行為的情況下研究研發網絡的風險傳播機制具有重要的理論和現實意義。

2 風險視域下下研發網絡的自適應演化

為了研究研發網絡中風險傳播與自組織演化之間的交互關系，首先我們需要構建一個虛擬的研發網絡。由于研發企業在研發網絡形成的過程中表現出擇優選擇意識，整體度分布呈現出冪率特征，因而具有無標度特性[14]；同時，企業之間的合作關系有強弱之分，因而可以看作加權網絡[7]。結合以上兩點特征，本文選用BBV模型構建研發網絡[15]。

(1)初始化：構建一個具有N0個節點的初始網絡，節點之間的邊權為w0。

(2)節點增加：每個時間步內加入一個新的節點j，其與已經存在的m個節點建立連接，每一條新邊同樣賦予權值w0。新加入的節點依據局域點權的比重與已有的節點建立連接，已有節點i與新加入的節點j建立連接的概率為：

其中si代表節點的點強度，其數值等于節點連邊權重的總和；τ表示網絡中除節點i之外所有節點的集合。

(3)邊權演變：一旦節點j與節點i建立新的連接，則節點i的點強度首先會增加w0，其次會有δ的增量，即：si→si+δ+w0，相連邊的邊權也會重新分配，即：wiτ→wiτ+Δwiτ，其中Δwiτ=δ×wiτ/si。

在研發網絡中，與處于危機狀態企業合作的正常企業可能會斷開彼此之間的合作關系來規避風險，之后正常企業會選擇其他的合作伙伴，建立新的合作關系，這就是企業為了規避風險的自適應行為。自適應行為中最重要的就是斷邊重連策略，即選擇什么樣的連邊斷開，選擇什么樣的關系建立新的連接關系。Gross等[10]基于SIS模型提出了節點數和連邊數不變情況下的隨機斷邊重連策略，認為網絡中的S-I連邊會以一定的概率斷開，其中S狀態的節點會隨機選擇非鄰居節點中的S狀態節點進行連接；Szabó[16]提出了一種獨立連接類型的斷邊重連策略，認為可以不考慮節點的類型，隨機從網絡中選取一組節點建立連接，之后再隨機選取一組連邊斷開，并基于SIS模型進行了分析；Risau-Gusman和Zanette[17]進一步豐富了斷邊重連策略，他們認為節點在斷邊重連時不一定完全了解全局狀態，因而I狀態的節點同樣可以隨機選擇節點進行重連；Shaw和Schwartz[18]以及Kiss等[19]基于SIRS模型分析了一直全局狀態信息下隨機斷邊重連策略以及其對網絡結構的影響。

在研發網絡中，由于信息的傳播以及企業自保意識對企業行為的影響，處于危機狀態的企業很難再次尋找到優秀的合作研發伙伴，優秀的研發企業往往也會避免與處于危機狀態的企業合作，因而文中假設只有處于正常狀態的企業才會建立新的連接，建立新的連接時也只會選擇正常狀態的企業。進而，假設研發網絡中企業的自適應行為不改變網絡的總節點數和總邊數，且不會產生重邊和自環，企業的自適應行為規則建模主要可以分為以下幾個步驟：

步驟一：選擇需要斷開的邊。將所有連接正常節點和感染節點的邊作為斷邊的候選集合Dcandidate，其中每一條邊都以概率p斷開連接。用(i,j)表示節點i和節點j之間的連邊，則時刻t可能會被斷開的邊的集合表示為：

Dcandidate

上述斷開連接的過程可以用函數表示為：在任意時刻t，對于邊(i,j)∈Dcandidate存在：

其中θ～U(0，1)，表示在(0，1)之間均勻分布的隨機數；斷邊概率p的實際涵義可以表示為研發網絡的組織治理水平，組織治理水平指的是企業具有自組織特性的自我治理水平，包括正式的契約治理以及非正式的關系治理。在理性假設的前提下，正常企業與合作企業中的感染企業斷開聯系的概率即可以表示為組織治理水平，組織治理水平高即表示企業具有更大的概率與感染企業斷開聯系，p值較大。

步驟二：將斷邊中的正常節點作為源節點發起新的連接。對于源節點i而言，新建立的連接關系與原有的連接關系質量和強度相同，能夠滿足源節點研發任務的需求，將源節點的非鄰居節點記為集合Lall，源節點可能會連接的節點看作候選節點集合Lcandidate，對于Lcandidate的界定可以分為兩種策略，分別為C1和C2。此外，策略C0表示靜態網絡，即不考慮斷邊重連的情況，在此作為對比實驗。

C1策略指的是將源節點i的所有非鄰居節點中度最大的節點作為Lcandidate，即可以表示為：

Lcandidate={j|z=max{kj}，j∈Lall}

C2策略指的是將源節點i的所有非鄰居節點中距離源節點最近的節點作為Lcandidate，本文采用的是相似權賦權方式，因而節點之間的距離可以用dij=1/wij表示，節點之間的距離可以直接相加，任意一組節點對之間的距離為網絡中節點之間最短路徑的長度，通過Floyd算法可以計算得出，即可以表示為：

Lcandidate={j|z=min{dij}，j∈Lall}

對于任何一種策略而言，Lcandidate中如果存在多個節點則隨機從中選取一個節點作為被連接節點，重新建立連接關系之后即有aij(t)=1且aji(t)=1，三類策略如表1所示。

表1 研發網絡自適應斷邊重連策略與參數設置

對于任意時刻t+1而言，其網絡的拓撲結構都與網絡在t時刻的拓撲結構以及時刻t網絡的狀態轉變相關。

B(t+1)=F(B(t),S(t+1))

3 基于SIS模型的研發網絡風險傳播模型

傳染病模型作為研究疾病傳播的科學方法，已經被廣泛應用于傳播動力學，較為典型的有SI、SIS以及SIR模型，其對于信息、謠言以及風險的傳播具有較好的實用性[20-22]。本文認為研發網絡中的企業被感染風險之后有一定的概率恢復正常，之后仍有可能被再次感染風險，因而SIS(susceptible-infected-susceptible)模型具有較好的適用性。

將研發網絡中企業的狀態分為兩個類別，分別是S態(易感狀態或者正常狀態)和I態(感染狀態)。S態代表企業未受到負面影響，研發狀態良好；I態代表企業受到市場環境變化等帶來的負面影響，研發績效較低。在任意一個時間間隔內，處于S態的企業都以概率V1被感染為I態，處于I態的企業都以概率V2恢復為S態，節點之間的狀態轉變關系如圖1所示。

圖1 節點狀態轉變規則

SIS模型的假設以及相關說明設定如下：

(1)研發網絡中的節點代表研發企業；研發網絡中的邊代表企業之間和合作關系；邊權代表合作關系的緊密程度，基于相似權的賦權方式，邊權越大代表企業之間合作關系越緊密。

(2)研發網絡風險傳播過程中考慮企業的自適應行為，且認為企業均能較快的獲取合作企業的動態信息，因而在初始時刻進行節點攻擊之后首先考慮企業的自適應行為過程，其次是風險傳播過程，之后的每個時間間隔均按照此順序執行。

(3)研發企業的狀態可以用數字進行量化分析，節點i在時刻t的狀態可以用Si(t)表示，S態和I態對應的數值分別為0和1。

時刻t，對于任意處于S態的企業，均會以概率V1被相鄰企業中處于I態的企業感染為I態。結合研發企業的異質性，概率V1與企業之間的合作程度有關，企業間合作程度越緊密則被感染的概率越高；概率V1與被感染企業的度有關，被感染企業的度越大則越容易被感染[23]。結合以上分析，本文將處于I態企業i感染相鄰企業j的概率V1設定為：

其中ψ(0<ψ<1)為控制參數，數值越大則表示節點間狀態傳染越容易，對應到研發網絡中即表示網絡組織間依賴水平，是敏感性依賴和脆弱性依賴兩個維度的集成體現[24]；wij表示節點i和節點j之間連邊的邊權；kj表示節點j的度，α為可調參數。

另外，對于任意處于I態的企業，均會以概率V2恢復為S態。結合研發企業的異質性，概率V2與網絡構建成本μ相關，網絡構建成本μ越大則企業恢復概率越大；同時，概率V2還與企業的重要度Φ相關，企業的重要度越高則可以調配的資源越多，恢復概率也就越大。

研發網絡中企業的重要度可以用K-shell模型來界定[25-26]，通過企業所處的網絡位置賦予企業特定的k-shell值來表征企業的位置重要度；結合無標度網絡的特征，引入局域邊權對k-shell值的影響[27]。綜合以上分析，將企業的恢復概率V2界定為：

V2=μ×φ

其中r和q為可調參數，控制著k-shell值和邊權的比重。

依據以上節點狀態轉變規則以及相關函數的界定，本文中基于SIS模型的研發網絡風險傳播模型整體的狀態轉變方程為：

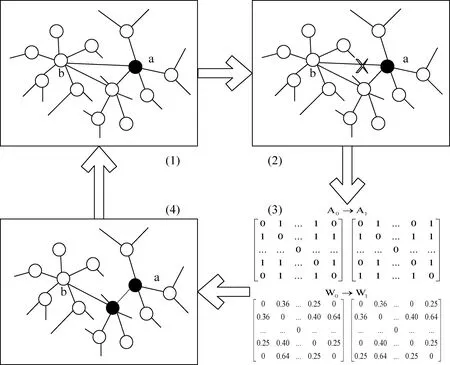
圖2 研發網絡中風險傳播與自適應演化的交互作用

其中θ～U(0，1)，表示在(0，1)之間均勻分布的隨機數。

任意時刻t，研發網絡中處于感染狀態企業個數的比例為I(t)，將風險傳播至穩態時研發網絡中處于感染狀態節點的比例定義為I*，其中I(t)可表示為：

研發網絡風險傳播模型充分體現出節點狀態的轉變與網絡拓撲結構之間的關系。對于任意節點i而言，t+1時刻的狀態與其在t時刻的狀態以及其在t時刻的拓撲結構相關，即：

S(t+1)=E(B(t),S(t))

綜合以上分析，研發網絡的風險傳播過程與自適應演化過程之間的關系如圖2所示。其中(1)表示初始狀態節點a處于感染狀態；(2)表示合作伙伴b與企業a斷開合作；(3)表示網絡鄰接矩陣以及邊權矩陣的變化；(4)表示節點a無法感染節點b，但是可以感染其他合作伙伴。

4 仿真分析

結合前文的分析，首先根據BBV模型構建研發項目網絡，節點個數N=1000，w0=1，m=1，初始時刻隨機選取比例為10%的節點將其狀態設為感染狀態，其余節點均為正常狀態；ψ=0.4，α=0.5，r=q=0.5，μ=0.6，p=0.6。鑒于不同的斷邊重連策略、不同的斷邊重連概率p以及不同的控制參數ψ等均會對研發網絡風險傳播過程造成影響，因此本文分別從不同的斷邊重連策略、斷邊重連策略對網絡結構的影響、不同的斷邊重連概率p以及不同的控制參數ψ研發網絡風險傳播的影響四方面進行數值仿真分析。

4.1 不同重連策略下研發網絡風險傳播過程

結合C0、C1和C2三種策略分別對研發網絡風險傳播過程進行仿真分析，經過100次仿真求平均值，結果表示如圖3所示。

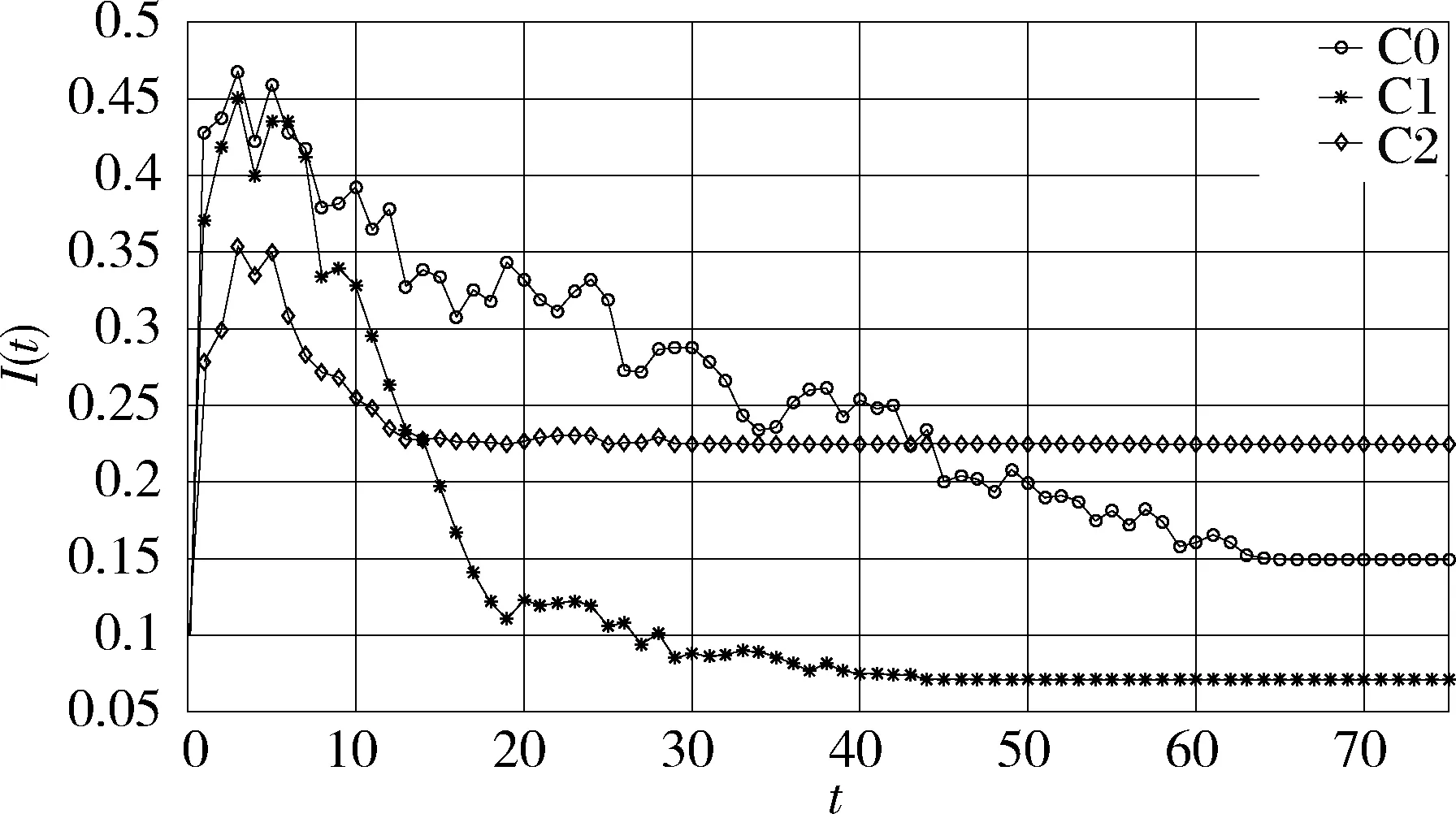
圖3 不同重連策略下研發網絡風險傳播過程

由圖3可知，在考慮研發網絡企業自適應行為的情況下，研發網絡的風險傳播過程呈現出不同的特征。從整體看，研發網絡風險傳播過程本質上體現的是企業感染狀態的傳導過程。從自組織理論層次性的角度來說，初始時刻處于感染狀態的企業首先會影響到具有主導地位的核心企業，使之成為感染狀態再次傳導的源頭，進而波及與其進行技術合作的相關企業導致局部耦合，擴大了感染狀態傳導的效應，感染狀態的企業的比例開始快速上升；而此后，從協同理論的角度進行分析，感染節點比例的上升推動了研發網絡自組織結構演變分化，破壞了網絡中的關鍵節點和關鍵路徑，阻斷了網絡風險傳播的核心路徑，因而網絡中的企業開始逐漸進行狀態恢復，處于感染狀態的企業比例逐漸降低；此后，網絡結構逐漸穩定，各企業保持特定的狀態，感染狀態的傳導告一段落。

在C1策略下，研發企業會選擇與網絡中度大的節點進行重連，增強了網絡的層次性和社團強度，使得網絡中的社團結構更加明顯，即未被感染的節點圍繞著若干度大的核心節點形成核心—邊緣結構，這種網絡形態一定程度上抑制了研發網絡中風險的傳播，所以圖3.1中C1策略下的感染節點的比例始終是低于C0狀態下的數值，可見C1策略是可以采取的一種研發網絡風險傳播的策略。

而對比C2策略和C0策略可知，C2策略下風險傳播的峰值是低于C0策略的，但是傳播至穩態時網絡中處于感染狀態的節點比例為0.225，明顯高于C0策略下穩態時的0.15，這與自適應行為的通常表現結果相悖。其中可能的原因是基于網絡臨近性的重連策略雖然也會促使網絡社團結構的增強，但是由于節點之間新連接的建立更多是基于臨近性的考量，容易陷入路徑依賴和能力陷阱，企業之間的知識同質化較強導致企業之間的信息溝通能力和合作效率降低，進而同時降低了企業之間的風險傳染概率和風險恢復概率，所以C2策略下的風險傳播峰值降低，同時穩態時的I*處于較高的水平；此外，C2策略下I*的數值較大還可能與斷邊的概率p等參數相關，比如斷邊的概率p與網絡的自適應結構演化有較強的相關性，在后續的研究內容中會對此進行進一步仿真分析和解釋說明。

4.2 斷邊重連對網絡屬性的影響

為進一步展現斷邊重連策略對研發網絡結構屬性的影響，選取C1策略下研發網絡風險傳播過程中的三個時間節點的網絡狀態，分別取t=0、t=35以及t=70，將各時刻對應的網絡數據輸入Gephi軟件進行網絡可視化處理，并結合平均路徑長度以及平均聚類系數兩個典型的網絡拓撲結構指標進行分析，如圖4所示。

圖4 不同時間段研發網絡拓撲結構的變化

如圖4以及表2所示，在t=0時刻，網絡拓撲結構呈現典型的小世界特性，且是一個全聯通的結構，較大的平均聚集系數以及較短的平均路徑長度有助于促進研發企業之間進行信息傳遞與合作交流；在t=35時刻，由于自適應行為的發生，網絡的拓撲結構在風險傳播過程的影響下出現裂變，部分小團體逐漸拉大與網絡和新結構之間的距離，但此時仍為全連通圖，平均路徑長度減小，且聚類系數明顯增大，這表明此時為網絡社團結構較明顯的時期，即社團強度較大，這種網絡結構一定程度上抑制了風險的傳播；在t=70時刻，風險傳播過程已經發展至穩態，網絡中已經有部分節點由網絡中分離出去，原因就是因為這部分節點感染風險之后相連節點斷開合作關系將其孤立而導致的。此時的平均聚類系數相比于t=35時刻有所下降，但是相比于t=0時刻仍然有較大的提升，可見自適應行為會導致社團強度的漲落。平均路徑長度的下降充分體現出C1策略的有效性，網絡中節點間信息傳輸以及溝通的效率得到優化，雖然風險傳播影響了節點的狀態，但是自適應行為優化了網絡資源的配置從而彌補了風險傳播帶來的損失。

4.3 不同斷邊概率p對研發網絡風險傳播的影響

斷邊重連概率p對風險傳播過程具有重要影響，分別在C1以及C2策略下針對不同斷邊重連概率p進行仿真分析，經過100次仿真求平均值，結果表示如圖5所示。

圖5-1 C1策略下不同斷邊概率p對研發網絡風險傳播的影響

圖5-2 C2策略下不同斷邊概率p對研發網絡風險傳播的影響

由圖5-1可知，在C1策略下，斷邊概率p與穩態時網絡中被感染的企業比例I*之間呈現“U”型相關關系，當p<0.7時，隨著p值的增大，I*逐漸降低，當p>0.7時，隨著p的增大，I*逐漸增大，當p值為0.7時，I*的數值最小。在一定范圍內，隨著組織治理水平的提升，研發網絡中的風險傳播明顯會收到抑制，這主要是研發企業會通過設置特定條件下的靈活性契約文件規范合作雙方的權利和義務從而盡可能在任何狀況下保全企業自身的利益，同時也體現在企業會保持充分的信任和溝通從而及時掌握合作企業的研發現狀，通過以上措施企業可以及時識別合作企業的研發狀態，當其被風險感染時可以暫時采取中斷合作研發關系尋求其他研發伙伴的策略規避風險可能造成的負面影響。此外，如果企業的組織治理水平超過合理水平的話反而不會為企業帶來更好的抗風險效果，過于靈活的契約文件可能會導致合作雙方的機會主義行為，也難以實現企業利益和網絡整體利益的辯證統一；同時，對于合作企業研發狀態過于敏感或者規避風險意識過于強烈的話會導致合作雙方的不信任，不利于對風險傳播的抑制。

在C2策略下斷邊概率p與穩態時網絡中被感染的企業比例I*之間的關系與C1策略有明顯的不同，隨著斷邊概率p的增長，穩態時網絡中被感染的企業比例I*逐漸降低。組織治理水平的提升對于研發網絡中的風險傳播的抑制作用與C1策略下的機理相通，不同的地方就在于C2策略下只有當組織治理水平處于較高水平時(p=0.9)才能夠實現與C0策略對比下的風險傳播抑制效果，而當p<0.9時，基于臨近性的斷邊重連策略無法起到抑制網絡中風險傳播的效果，可見大多數情況下C2策略并不能夠有效的抑制研發網絡的風險傳播。

4.4 不同ζ值對研發網絡風險傳播的影響

不同ζ值(組織依賴水平)對風險傳播過程具有重要影響，分別在C1以及C2策略下針對不同ζ值進行仿真分析，經過100次仿真求平均值，結果表示如圖6所示。

圖6-1 C1策略下不同ζ值對研發網絡風險傳播的影響

圖6-2 C2策略下不同ζ值對研發網絡風險傳播的影響

由圖6-1和6-2可知，無論是在C1策略下還是在C2策略下，隨著參數ζ的增長，穩態時網絡中處于感染狀態的節點比例I*也隨之增長。在C1策略下，無論參數ζ取何值，最終均會有效抑制研發網絡風險傳播過程，這再一次驗證了C1策略的有效性和適用性；而在C2策略下，參數ζ在[0.1，0.4]范圍內時可以在一定程度上起到對風險傳播的抑制作用，但是在[0.5，0.9]范圍內則無法實現對風險傳播的抑制效果。組織間依賴水平的提升致使合作企業之間更強的敏感性和脆弱性[28]，引發合作企業之間合作行為的調整，當合作企業感染風險之后就更有可能受到其造成的負面影響也被感染風險，即增大了企業之間風險狀態傳染的概率。隨著組織間依賴水平的提升，風險傳播至穩態時網絡中處于感染狀態的企業比例也就越多，可見組織依賴水平是研發網絡風險傳播控制中需要重點關注的因素。

5 結語

本文基于風險視域下研發網絡企業狀態的變化和網絡結構的變化相互耦合機理，在考慮自適應行為的情況下研究研發網絡的風險傳播機制，根據BBV模型生成研發網絡，構建研發網絡企業自適應行為規則，提出基于節點度和節點間距離的兩類斷邊重連策略，基于SIS模型構建研發網絡風險傳播模型，運用數值仿真的方法通過改變模型參數探索在考慮自適應行為的情況下研發網絡的風險傳播規律，研究結果表明：(1)在C1策略下，研發企業會選擇與網絡中度大的節點進行重連，增強了網絡的層次性和社團強度，這種網絡形態一定程度上抑制了研發網絡中風險的傳播；C2策略雖然也會促使網絡社團結構的增強，但是由于節點之間新連接的建立更多是基于臨近性的考量，容易陷入路徑依賴和能力陷阱，企業之間的知識同質化較強導致企業之間的信息溝通能力和合作效率降低，風險傳播峰值降低，同時穩態時的I*處于較高的水平；(2)研發網絡企業的自適應行為會導致社團強度的漲落，平均路徑長度的下降以及平均聚類系數的增長充分體現出C1策略的有效性，網絡中節點間信息傳輸以及溝通的效率得到優化，自適應行為優化了網絡資源的配置從而彌補了風險傳播帶來的損失。(3)C1策略下，斷邊概率p與穩態時網絡中被感染的企業比例I*之間呈現“U”型相關關系；在C2策略下隨著斷邊概率p的增長，穩態時網絡中被感染的企業比例I*逐漸降低。(4)在C1策略下還是在C2策略下，隨著參數ζ的增長，穩態時網絡中處于感染狀態的節點比例I*也隨之增長，組織依賴水平是研發網絡風險傳播控制中需要重點關注的因素。本文進一步揭示了在考慮自適應行為的情況下研究研發網絡的風險傳播規律，為網絡化運作背景下研發網絡治理提供理論依據。