變量隨機性的游程檢驗與SPSS實現

楊吉會

【摘要】非參數檢驗是數據統計分析方法的重要組成部分，它與參數檢驗方法共同構成了統計推斷理論的核心內容.游程檢驗是一種常用的非參數檢驗方法，在眾多數據統計問題中都有應用，恰當的理解和運用該數據分析方法，以及掌握其在數據統計軟件中的實現過程，對課堂教學和科研工作都具有現實意義.本文結合SPSS軟件的使用，闡述游程檢驗在數據分析過程中的使用方法，并通過具體實例說明該非參數檢驗方法的有效性和可行性.

【關鍵詞】隨機性;非參數檢驗;游程;SPSS軟件

【基金項目】國家自然科學基金（41401322）.

一、單樣本的游程檢驗

非參數檢驗是數理統計學的一個重要研究內容，是相對參數檢驗提出的概念.參數檢驗是在已知總體分布的環境下，對總體分布參數進行推斷的方法.非參數檢驗是在對總體分布的具體形式未知或不是充分了解的情況下，從樣本的數據獲得需要的信息，對總體分布的類型或總體的其他統計特性進行檢驗的方法.根據樣本數據的來源，主要包括有單樣本的非參數檢驗，多獨立樣本的非參數檢驗、多配對樣本的非參數檢驗等[1].針對不同類型的問題提出了不同的非參數檢驗方法，其中游程檢驗是一類經常使用的非參數檢驗方法，其理論的出發點是檢驗樣本的獨立性，即檢驗數據的出現順序是否是隨機的[3-5].這一點非常重要，因為，許多遇到的實際問題中并不只是使研究者關心分布的位置或者形狀，也包括樣本的隨機性，絕大部分經典統計方法在理論上都要求樣本具有隨機樣本，即要求重復觀察到的一組變量值在統計上具有獨立性，如果樣本不是從總體中隨機抽取的，則所做的任何推斷都將沒有價值.游程檢驗是最簡單的判斷樣本取值順序是否具有隨機性的非參數檢驗方法.本文通過SPSS軟件的使用，通過實例說明這種非參數檢驗的使用過程.

所謂游程是樣本序列中連續出現的變量值的次數r，特別地，在一個0/1序列中，一個由0或1連續構成的串稱為一個游程，一個游程中數據的個數稱為游程的長度.

一個樣本序列的游程個數用r表示.例如，我們投擲一枚硬幣，獨立重復的進行25次投擲，得到如下的0/1序列：

0000000111111000011110000

上述序列中有3個0游程，長度分別為7、4、4，2個1游程，長度分別為6和4，序列的游程數r=5.顯然，該序列0的總個數為n1=15，1的總個數為n2=10，總的試驗次數n=n1+n2=25.

一般的，若一個樣本序列具有隨機性，則這個樣本序列的游程數不能太多，也不能太少.當樣本序列的長度n1和n2已知時，樣本序列的游程數r近似服從正態分布，且有

下面通過具體例子說明利用SPSS軟件對單個樣本變量取值的隨機性進行游程檢驗的過程.

例1 為檢驗某耐壓設備在某段時間內工作是否持續正常，測試并記錄下該時間段內各個時間點上的設備耐電壓值的數據如下表：

現利用游程檢驗法對這批數據進行分析，判斷該設備工作是否正常.

解 如果耐壓數據的變動是隨機的，可認為該設備工作一直正常，否則認為該設備有不能正常工作的現象.因此，檢驗的原假設H0為該設備的耐壓值是隨機的，即該設備工作基本是正常的，備擇假設H1為該設備的耐壓值不具有隨機性，即該設備有不能正常工作的現象.不妨取數據的中位數204.55為檢驗值，小于檢驗值的數據為第1組，大于等于檢驗值的數據為第2組，由此形成由1與2構成的數據序列為

12122121111212122221

容易計算出該序列的游程數r=13，且第1組和第2組各有10個數據，即n1=n2=10，這是一個小樣本問題，則有

應用SPSS 23.0軟件求解過程如下：

（1）選擇菜單【分析（A）】→【非參數檢驗（N）】→【舊對話框（L）】→【游程（R）】.

（2）選擇待檢驗變量到【檢驗變量列表（T）】框中.〖HJ1.14mm〗

（3）【割點】框中選擇中位數作為分界值.

求解過程如下圖所示：

a.中位數

由以上結果可知，中位數204.55，共有20個觀測樣本.小于檢驗值與大于檢驗值的數目各為10，游程數為13，檢驗統計量的值為0.689，對應的概率P-值為0.491.若顯著性水平為0.05，由概率P-值大于顯著性水平，故應接受原假設，可以認為該設備在這段時間內工作是基本正常的.

二、兩獨立樣本的游程檢驗

單樣本的游程檢驗是用來檢驗單個變量的變量取值是否具有隨機性，兩獨立樣本的游程檢驗則是用來檢驗兩獨立樣本來自的兩個總體的分布是否存在顯著差異，這里以瓦爾德-沃爾福威茨游程檢驗為例進行討論，檢驗的原假設H0為兩獨立樣本來自的兩總體的分布沒有顯著差異，備擇假設H1為兩獨立樣本來自的兩總體的分布存在顯著差異.檢驗方法如下：

首先將來自兩總體的兩樣本按照變量值的升序排列，從而確定出組標記值的一個排列，針對該組標記值的這個排列按照單樣本游程檢驗的方法計算其游程數，如果兩總體的分布存在較大差異，則游程數會相對較小;如果游程數比較大，則表明兩總體的分布沒有明顯差異，最后利用公式（1）-（4）計算正態統計量Z獲得檢驗結論[6-8].

例2 在我國的工業和商業企業中隨機抽取22家企業進行資產負債率行業差異分析，抽樣獲得的兩類企業某年底資產負債率（% ）數據如下表：

試用兩獨立樣本的游程檢驗方法判斷工業企業與商業企業的資產負債率是否存在顯著差異.

解 原假設H0為兩類企業的資產負債率沒有顯著差異，備擇假設H1為兩類企業的資產負債率存在顯著差異.將兩類企業資產負債率數據由SPSS數據編輯器窗口錄入，工業企業的數據標記為第1組，商業企業的數據標記為第2組，通過SPSS【數據（D）】按鈕的【個案排序（O）】功能將資產負債率按照升序排列，由此形成由1與2組標記構成的數據序列為

1111121111222111222222

容易計算出該序列的游程數r=6，且第1組有12個數據，第2組有10個數據，即n1=12，n2=10，這是一個小樣本問題，則有

應用SPSS軟件求解過程如下：

（1）選擇菜單【分析（A）】→【非參數檢驗（N）】→【舊對話框（L）】→【兩個獨立樣本（2）】.

（2）選擇待檢驗變量到【檢驗變量列表（T）】框中.

（3）指定存放組標記值的變量到【分組變量（G）】框中，并點擊【定義范圍（D）】按鈕給出組標記值的取值范圍.

（4）在【檢驗類型】框中選擇【瓦爾德-沃爾福威茨游程（W）】檢驗方法.

求解過程如下圖所示：

SPSS運行結果如下：

由以上結果可知，共有22個觀測樣本.工業企業的個案數為12，商業企業的個案數為10，游程數為6，檢驗統計量的值為-2.384，對應的概率P-值為0.008.若顯著性水平為0.05，由概率P-值遠小于顯著性水平，故應拒絕原假設，接受備擇假設，可以認為兩類企業的資產負債率存在顯著差異.

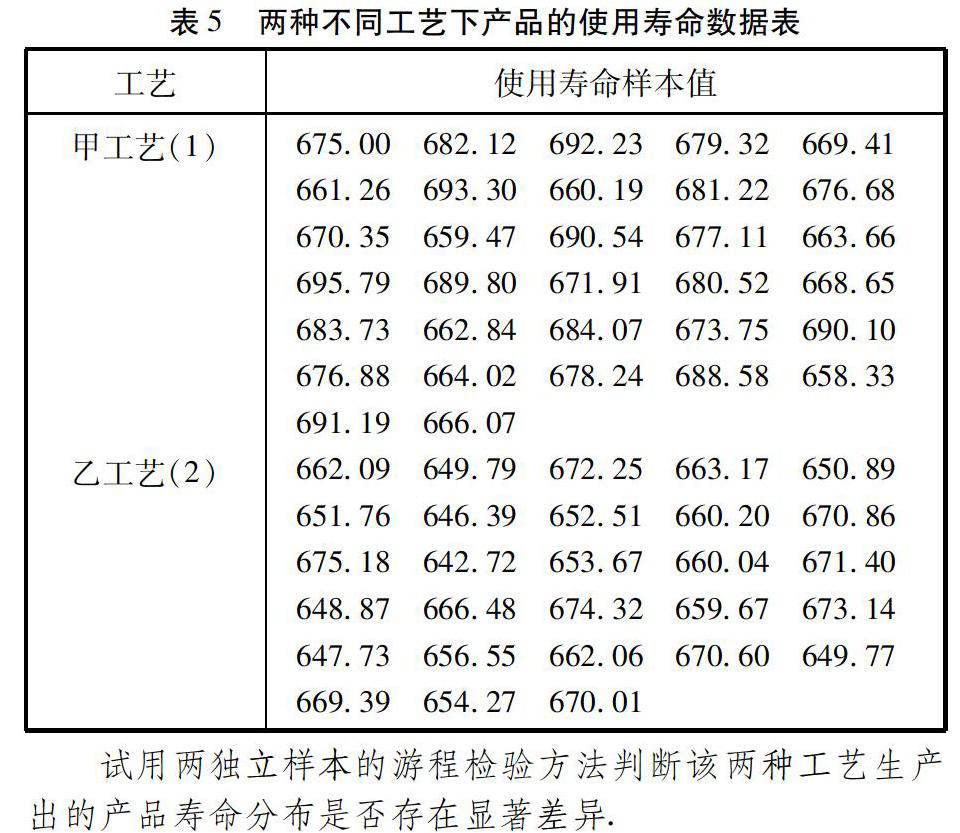
例3 某工廠用甲、乙兩種不同的工藝生產同一種產品，現從兩種工藝生產出的產品中隨機抽取60個產品，獲得各自的使用壽命數據如下表：

試用兩獨立樣本的游程檢驗方法判斷該兩種工藝生產出的產品壽命分布是否存在顯著差異.

解 原假設H0為兩種工藝生產出的產品壽命分布沒有顯著差異，備擇假設H1為兩種工藝生產出的產品壽命分布存在顯著差異.將兩種工藝生產出的產品壽命數據由SPSS數據編輯器窗口錄入，甲種工藝的數據標記為第1組，乙種工藝的數據標記為第2組，通過SPSS【數據（D）】按鈕的【個案排序（O）】功能將產品壽命數據按照升序排列，由此形成由1與2組標記構成的數據序列為

222222222222112212122121112121212221221212

111111111111111111

容易計算出該序列的游程數r=24，且第1組有32個數據，第2組有28個數據，即n1=32，n2=28，這是一個大樣本問題，則有

應用SPSS軟件求解過程如下：

（1）選擇菜單【分析（A）】→【非參數檢驗（N）】→【舊對話框（L）】→【兩個獨立樣本（2）】.

（2）選擇待檢驗變量到【檢驗變量列表（T）】框中.

（3）指定存放組標記值的變量到【分組變量（G）】框中，并點擊【定義范圍（D）】按鈕給出組標記值的取值范圍.

（4）在【檢驗類型】框中選擇【瓦爾德-沃爾福威茨游程（W）】檢驗方法.

求解過程如下圖所示：

SPSS運行結果如下：

由以上結果可知，共有60個觀測樣本.甲種工藝的個案數為32，乙種工藝的個案數為28，游程數為24，檢驗統計量的值為-1.796，對應的概率P-值為0.036.若顯著性水平為0.05，由概率P-值小于顯著性水平，故應拒絕原假設，接受備擇假設，可以認為兩種工藝生產出的產品壽命分布存在顯著差異.

【參考文獻】

[1]王星.非參數統計[M].北京：清華大學出版社，2009.

[2]薛薇.基于SPSS的數據分析（第四版）[M].北京：中國人民大學出版社，2017.

[3]孫建偉，許汴利，蘇佳，黃學勇.游程檢驗及其在流行病學中的應用與探討[J].預防醫學論壇，2017（2）：26-29，32.

[4]李學，劉建民，靳云匯.中國證券市場有效性的游程檢驗[J].統計研究，2001（12）：43-46.

[5]王靜茹，趙以立.游程檢驗應用[J].中國統計，1993（6）：44-45.

[6]朱凱李悅.RPT方法在多元游程檢驗中的應用[J].中國衛生統計，2016（2）：362-363.

[7]蘭嘉慶，余宛泠.異方差的游程檢驗[J].中山大學學報（自然科學版），2004，43（z1）：9-11.

[8]Alhakim，A，Hooper，W.A non-parametric test for several independent samples[J].Journal of Nonparametric Statistics，2008（20）：253-261.