從Euler公式談談冪指函數的自然定義域
秦玉鵬 范三妞


【摘要】針對現行教材冪指函數自然定義域尚不清晰問題,本文將實數域分為若干情形進行討論,并借助Euler公式明確給出了冪指函數的自然定義域.作為應用,指出在對冪指函數施行對數求導法之前應先熟知冪指函數的自然定義域,而非直接對其施行對數求導,以確保數學之嚴謹性,使大一新生對冪指函數及對數求導法有一個更清晰更全面的認識.
【關鍵詞】冪指函數;自然定義域;實數域;Euler公式;對數求導法
【基金項目】河南省教科規劃一般課題“新時代背景下基于DBL的數學創新能力培養策略研究”〔2019〕-JKGHYB-0240;河南工學院博士科研啟動基金(KQ1860).
一、引 言
指數和底數都是變量的,形如
f(x)=u(x)v(x)(x∈E,E是數集)(1)
的函數稱為冪指函數,其中u,v是E上的函數[1].通常情況下,當不給出u(x)和v(x)的具體形式時,總要求u(x)>0(x∈E),此時冪指函數可改寫成
從而當u,v連續時它連續,u,v可導時它可導[1].(2)的形式在高等數學對數求導法中起到至關重要的作用[2],通常在做題時默認u(x)>0并直接對冪指函數進行對數求導,而細心的同學會發現直接默認u(x)>0是不合適的,因為當u(x)<0時,諸如x=-2這類點顯然也在冪指函數xx的自然定義域內,那么一般地,冪指函數的自然定義域是什么?在定義域內各類點處的可導性又如何呢?教材上并沒有給出明確的答案.
顯然,為了回答這個問題,必須首先弄清楚冪指函數的自然定義域,才能在此基礎上判斷各點的連續性,進而討論其可導性.因此,本文的主要目的就是探析冪指函數的自然定義域,并在此基礎上回答上述問題.
二、預備知識
本部分我們將借助Euler公式將對數函數做一個簡單推廣.
公式(3)被稱為歐拉恒等式,也被理查德·費曼稱為“最卓越的數學公式”.
本文從Euler公式的角度出發,不再限制對數函數lnx中的真數部分x>0,而將真數部分的定義推廣為x>0或x<0.如當x=-1時,借助公式(3)可得
同理,對一般的x<0,不難推出
三、關于數ab(a,b為實數)的一個定理
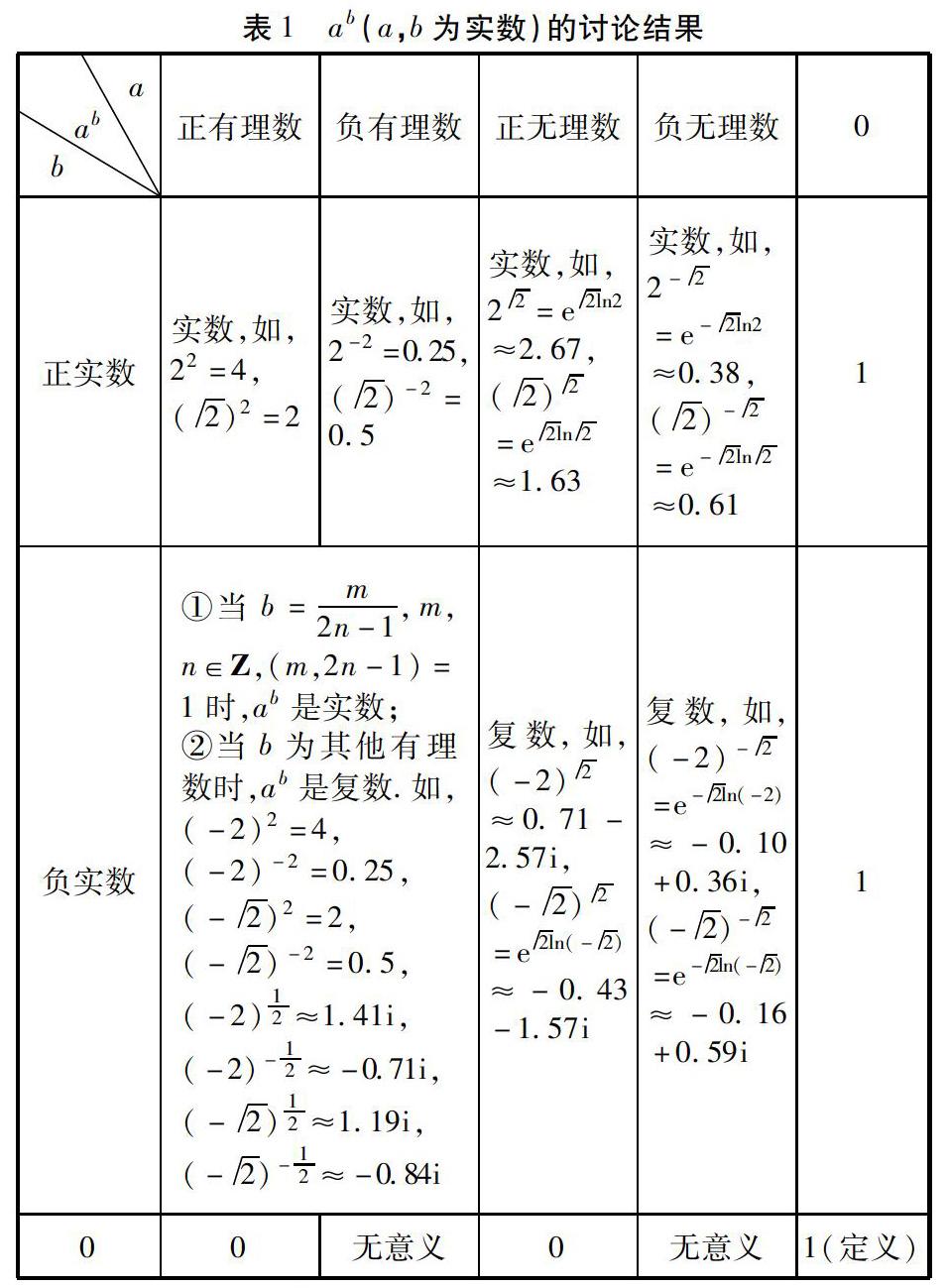
在探討冪指函數的定義域之前,我們先來討論下形如ab(a,b為實數)的數在a,b滿足什么樣的條件下為實數.
注意在以下討論中遵循:任意實數的0次冪等于1,即a0=1;0的正實數次冪等于零,0的負實數次冪無意義.討論結果和舉例詳見定理1和表1.
定理1 若實數a,b滿足下述三類情形之一:
(Ⅰ)底數a為正實數(a>0),指數b為任意實數;
(Ⅱ)底數a為負實數(a<0),指數b為滿足b=m 2n-1,m,n∈Z ,(m,2n-1)=1的有理數;
(Ⅲ)底數a=0,指數b為非負實數,則ab為實數.注意這里(m,2n-1)=1表示m與2n-1互質.
證明 我們的主要思想是通過遍歷a,b在實數域上的所有可能情形,即先將a在實數域上分為“正實數”,“負實數”和“0”三類情形,再將b在實數域上分為“正有理數”,“負有理數”,“正無理數”,“負無理數”和“0”五類情形進行分別討論.
情形1(a>0):
因為a>0是正實數,顯然,不論b是何種情形(正有理數,負有理數,正無理數,負無理數,或0),ab表示的都為實數.
情形2(a<0):
(ⅰ)當b為正有理數時,因為正有理數可表示為正分數(兩個正整數之比的數),則b可表示為“奇數/奇數”,“偶數/奇數”或“奇數/偶數”三種形式,若記
結合例1的討論,不難發現教材上在對形如(1)式的冪指函數施行對數求導時,默認u(x)>0這一前提條件并不會影響最終的求導結果,因為u(x)<0時對應的有定義的點都是孤立存在的,是一系列不可導點;而對u(x)=0時對應的有定義的點也是不可導點.
六、結 論
本文針對冪指函數在實數范圍內的自然定義域問題,通過將實數域分為若干情形進行了詳細討論,明確給出了其自然定義域,如定理2所示.將其應用于冪指函數的對數求導法,結果表明在利用對數求導法求解此類問題時,默認冪指函數底數大于零這一前提條件雖然并不影響最終結果,但是考慮到數學的嚴謹性,有必要在熟知了冪指函數的自然定義域之后再進行對數求導.筆者希望通過本文的討論,使大一新生對冪指函數和對數求導法有一個更清晰更全面的認識.
【參考文獻】
[1]《數學辭海》總編輯委員會.《數學辭海》第1卷[M].南京:東南大學出版社,2002:514-515.
[2]同濟大學數學系,高等數學(上冊):第七版[M].北京:高等教育出版社,2014:101-110.

